この記事では電気回路の一種であるRC直列回路の過渡現象について取り扱います。
RC直列回路のスイッチをONにした後の電流、電圧がどうなるのか、その傾向についてグラフを用いて説明します。
【まとめ】RC直列回路の過渡現象グラフ(スイッチON)
RC直列回路の過渡現象
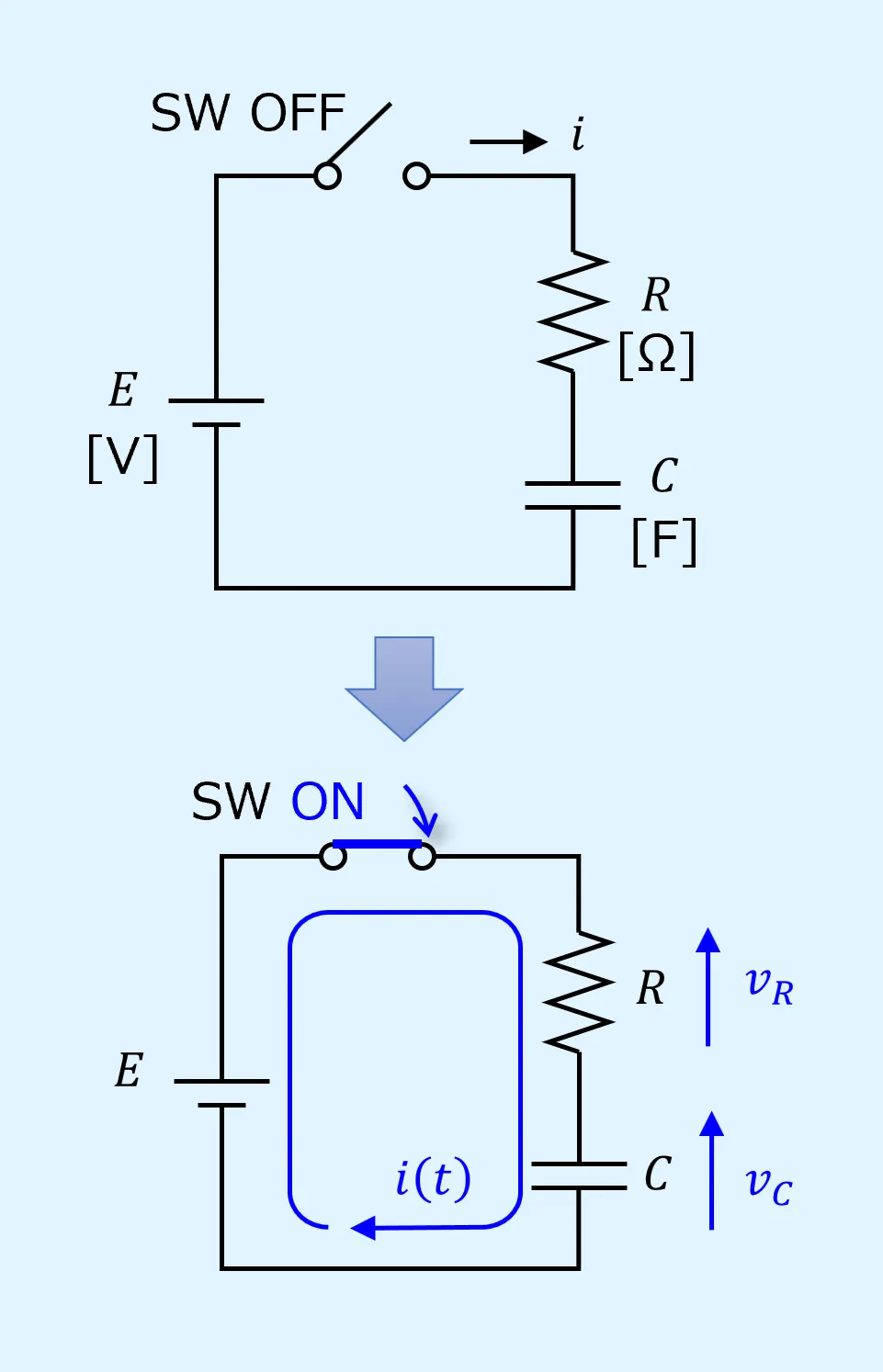
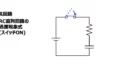
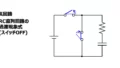
RC直列回路のスイッチをONにすると、空のキャパシタに電流が一気に流れ、電荷で満たされると流れなくなります。
これがRC直列回路のスイッチをONにしたときに生じる過渡現象です。
RC直列回路のスイッチをONにしたときの過渡現象における電流と電圧の式は以前の記事で導出しました。
本記事では導出した式をグラフにして過渡現象を視覚的に説明します。
電流のグラフ
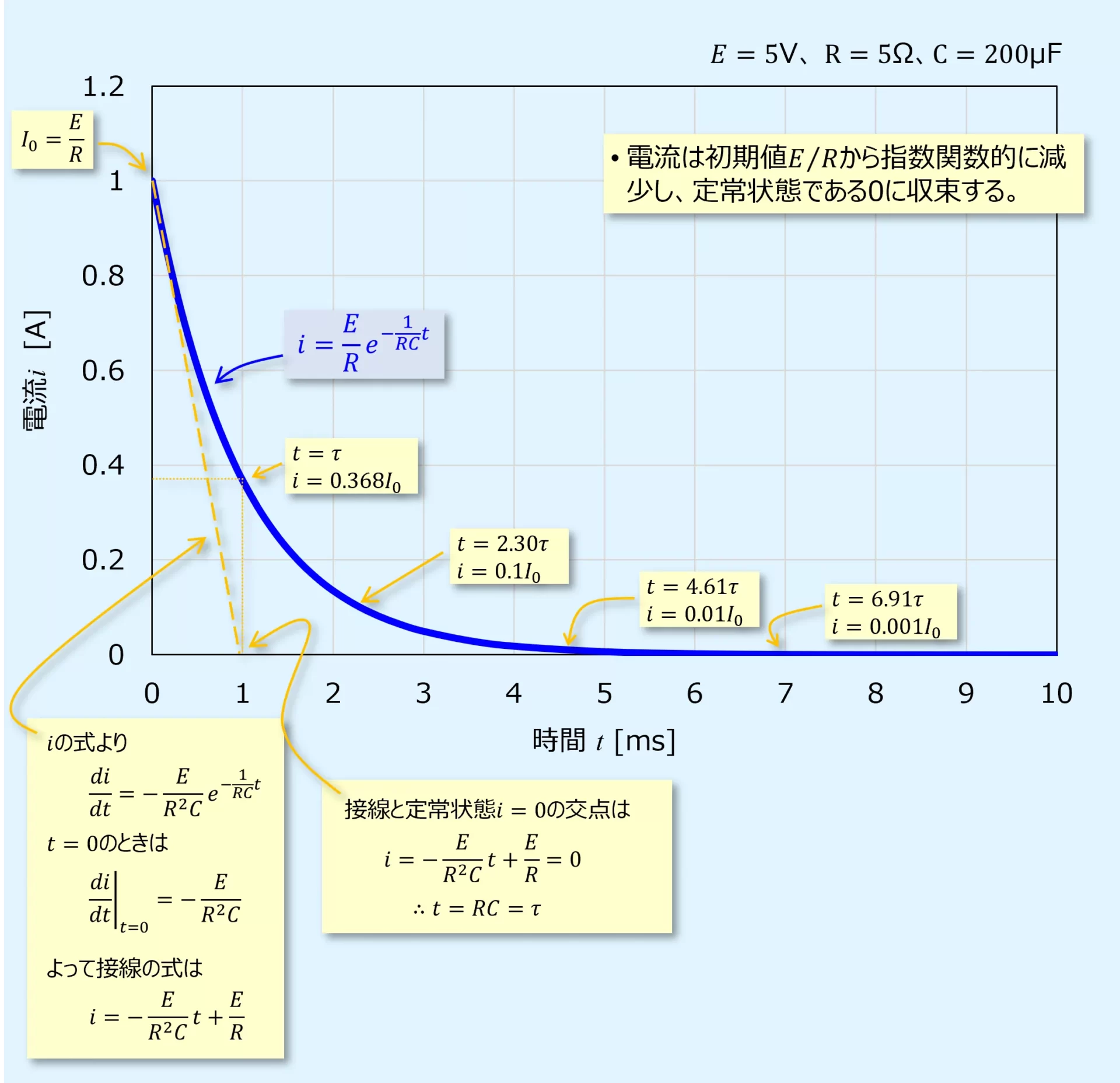
RC直列回路のスイッチをONにしたときの過渡現象における電流\(i\)の式は以下の通りです。
この式よりグラフは以下となります。
スイッチをONにした直後、初期状態の\(i\)は\(E/R\)[A]です。
空のキャパシタには抵抗によって制限された電流をそのまま流せるためです。
そこから指数関数的に減少し、定常状態である0[A]に収束していきます。
収束に要する時間は時定数\(\tau=RC\)に依存します。
感覚的に時定数の影響が分かるように、時間軸上に時定数が記載されていることがあります。
これはスイッチをONにした\(t=0\)のときの接線と時間軸の交点が\(\tau\)となるためです。
\(t=\tau\)のときのiは、中途半端ですが、初期値の0.368倍です。
定常状態がどこからか、という厳密な定義はありません。
しかし、有効桁数3桁で観測をしているなら、定常状態の0.001倍となる\(t=6.91\tau\)以降ですと測定結果に変化が無くなるため定常状態といって差し支えありません。
なお、定常値の0.1倍となるのは\(t=2.30\tau\)、0.01倍だと\(t≒4.61\tau\)です。
時定数の影響を見るために、キャパシタンスを変更した場合のグラフを以下に示します。
速くONへ切り替えるためには時定数を小さくするしかありません。
そのためには抵抗を小さくするか、キャパシタンスを小さくするかの2択となります。
要素の電源電圧、抵抗、キャパシタンスが異なっていても、初期値、時定数が同じになれば過渡現象は同じになります。
2.5V、2.5Ω、400μFの例を上記のグラフに加えて、以下に示します。
電圧のグラフ
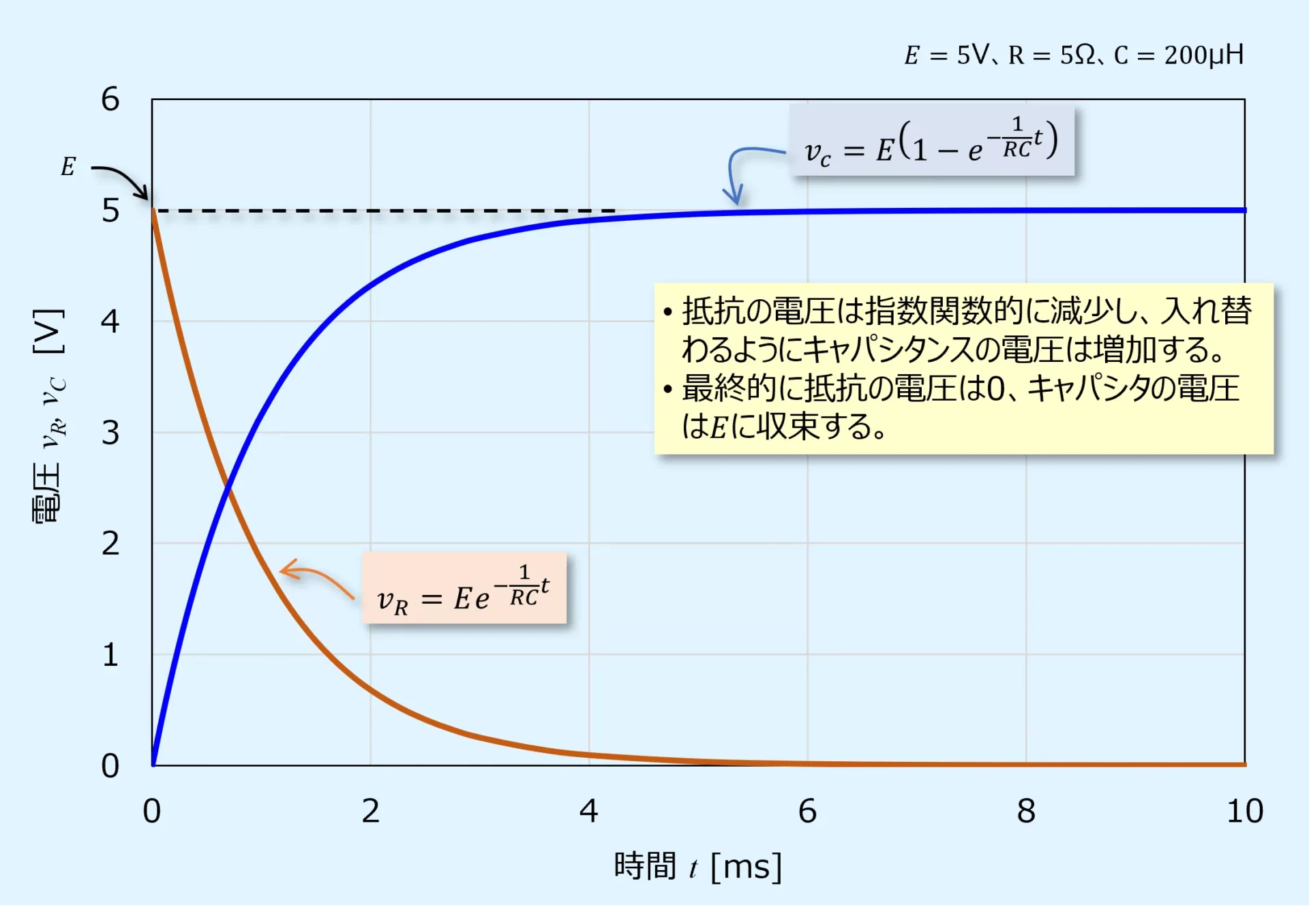
RC直列回路のスイッチをONにしたときの過渡現象における、抵抗とキャパシタの電圧\(v_R,v_C\)は次式で表されます。
上式より電圧のグラフは以下となります。
\(v_R\)は\(i\)と同様で、初期に大きく、その後は指数関数的に減少し、0[V]へ収束していきます。
\(v_C\)は初期の0[V]から、キャパシタに電荷が溜まるに従い大きくなり、定常値の\(E\)[V]に収束します。
その他
電気回路全般については以下をご覧下さい。





コメント