この記事では電気回路の無効電力を取り扱います。
無効電力の定義と、無効電力とは何なのかについて説明します。
【まとめ】無効電力
最初にまとめです。
はじめに
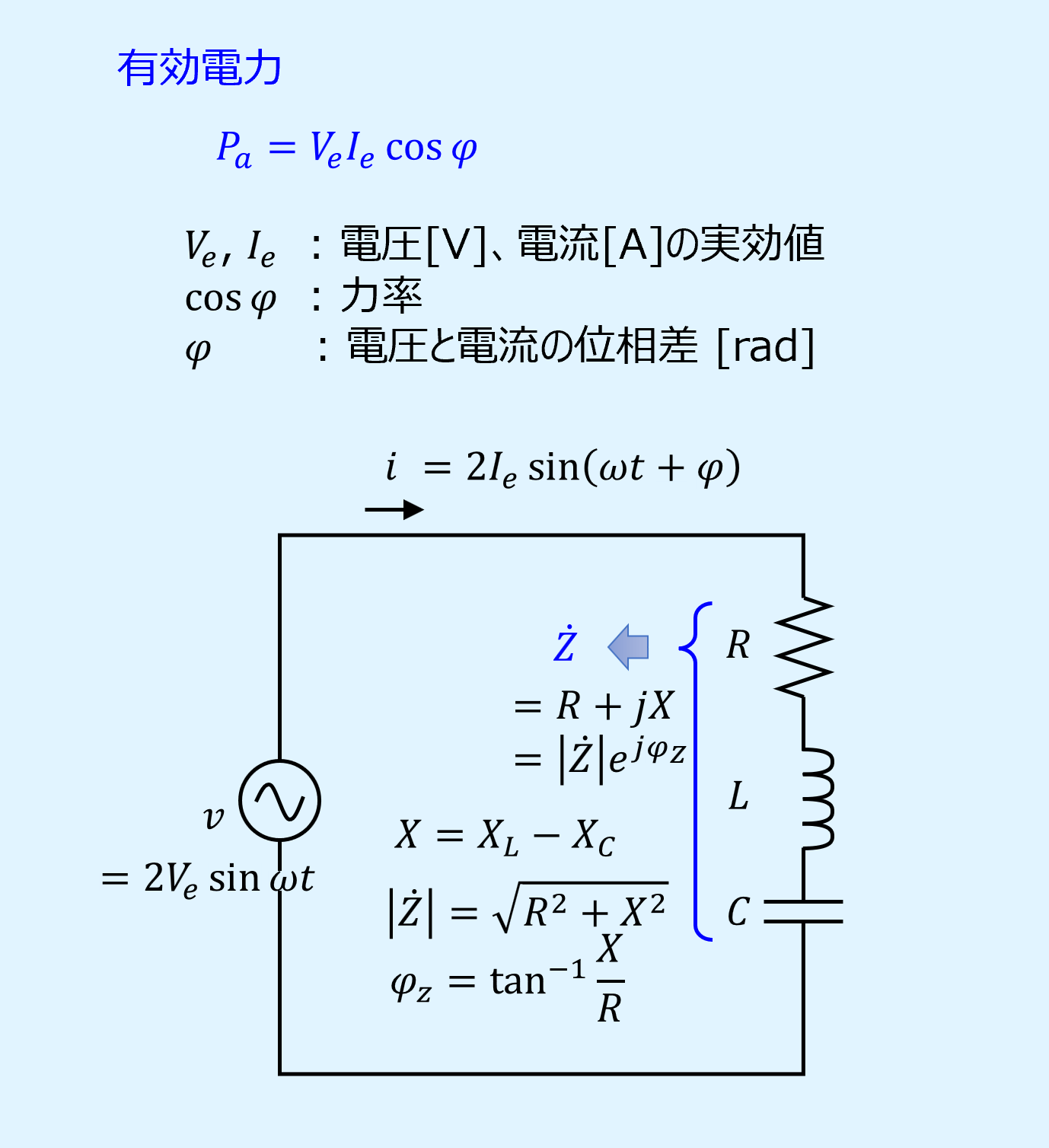
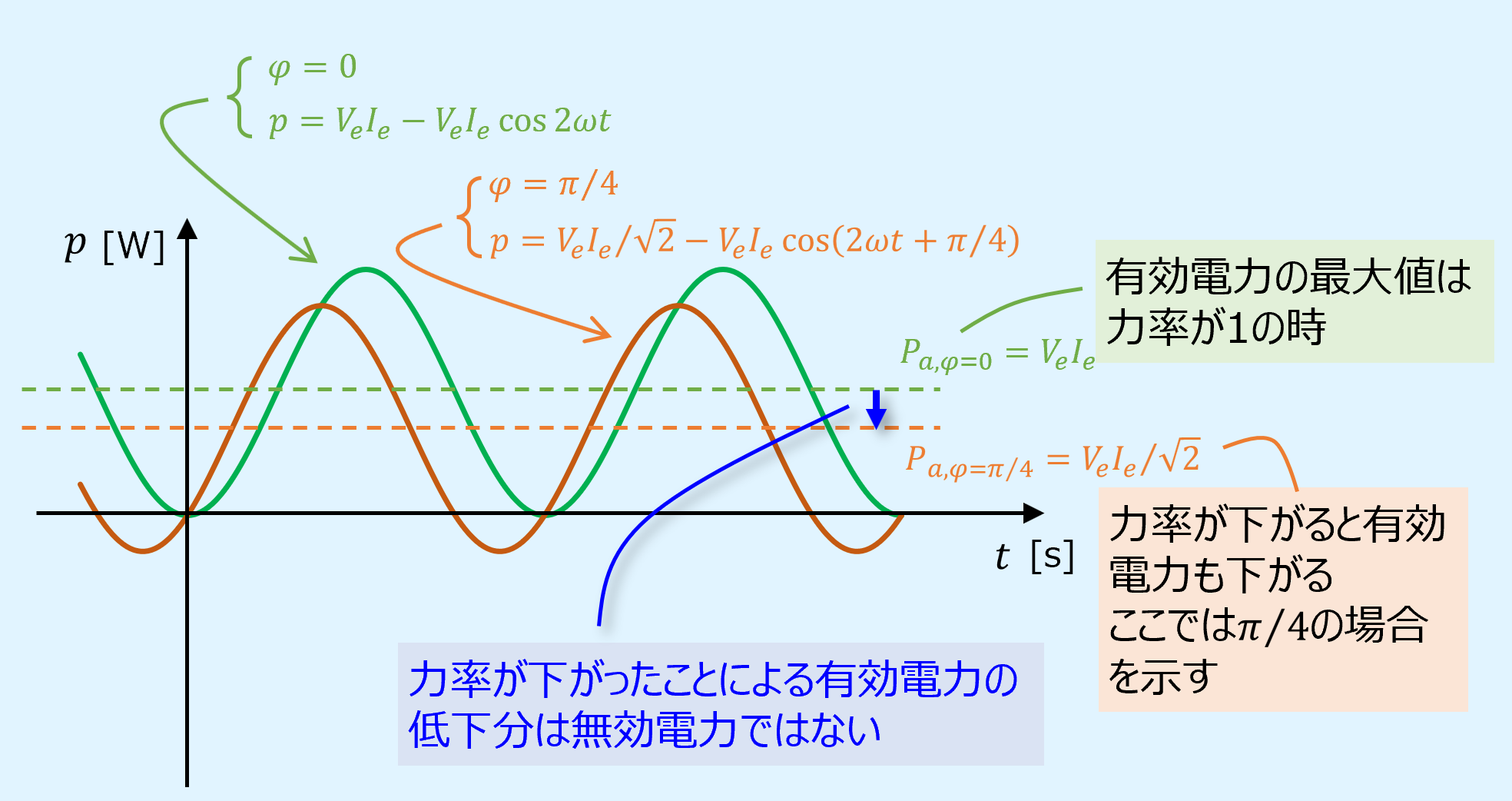
負荷にインダクタ、キャパシタ等のリアクタンス成分\(X\)を含み、電圧と電流に位相差が生じる交流回路において、有効電力\(P_a\)[W]は力率\(\cos\varphi\)を用いて、次式で表されます。
上式から、力率が小さくなると有効電力も小さくなることが分かります。
力率は\(\varphi\)が\(\pm\varphi/2\)の時に最小の0となります。
では、有効電力の最大値\({\max}P_a=V_eI_e\)と有効電力\(P_a\)の差分\(V_eI_e(1-\cos\varphi)\)が無効電力でしょうか。
答えは否で、消費されない電力という意味ではありません。
以降で無効電力の定義と、そもそも何なのか、なぜそのように定義されるのかについて説明します。
無効電力の定義
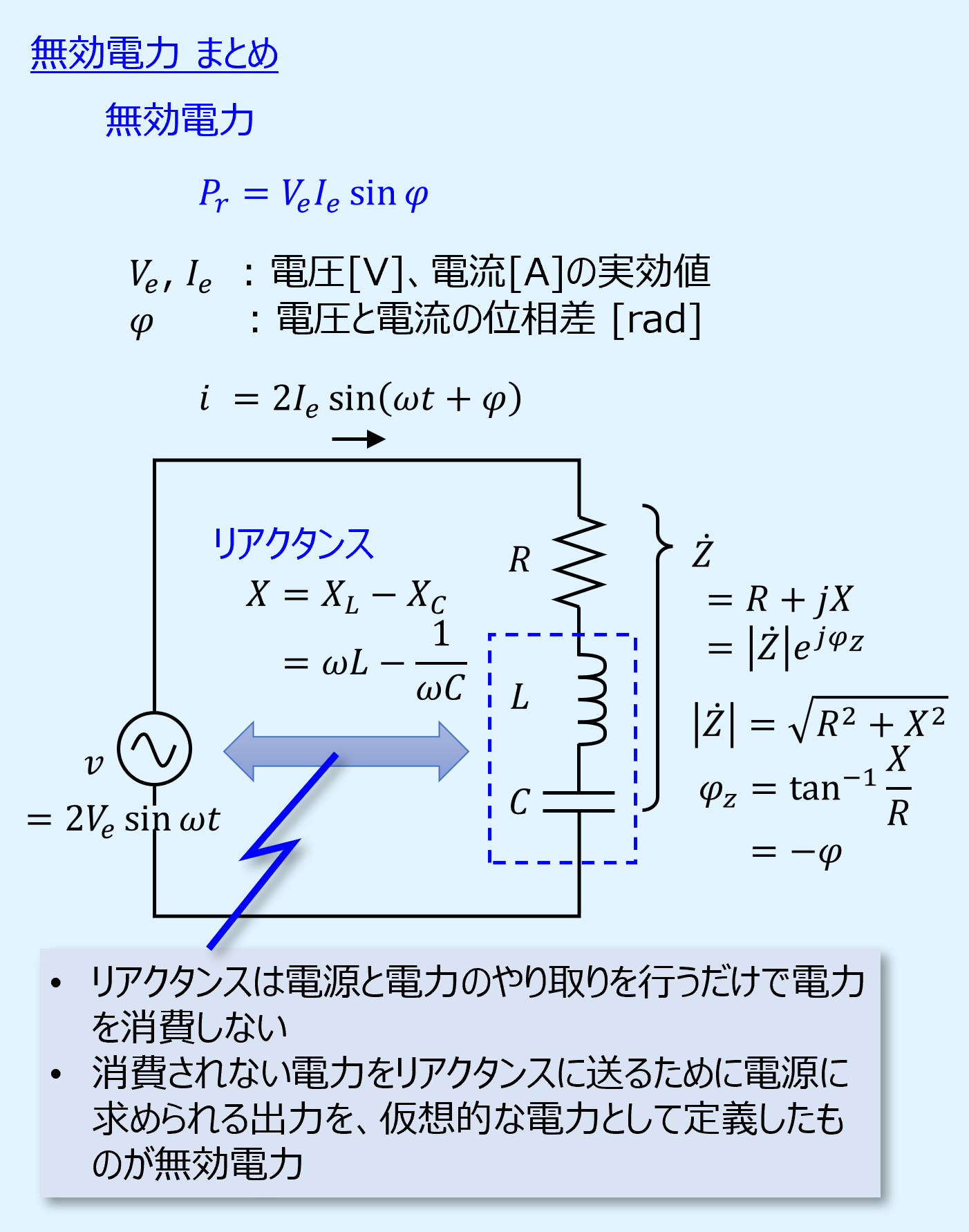
無効電力(reactive power)は次式で定義されます。
単位は[var]で、「バール」と読みます。
[W]でない点に注意しましょう。
無効電力は位相¥(\varphi\)が\(-\pi/2\)のとき、最小値の\(-V_eI_e\)となり、0のとき、0となり、\(\pi/2\)のとき、最大値の\(V_eI_e\)となります。
式自体は簡単で覚えやすいですが、これでは無効電力とは何か、なんでこう定義されるのかが全く分かりません。
無効電力とは何か
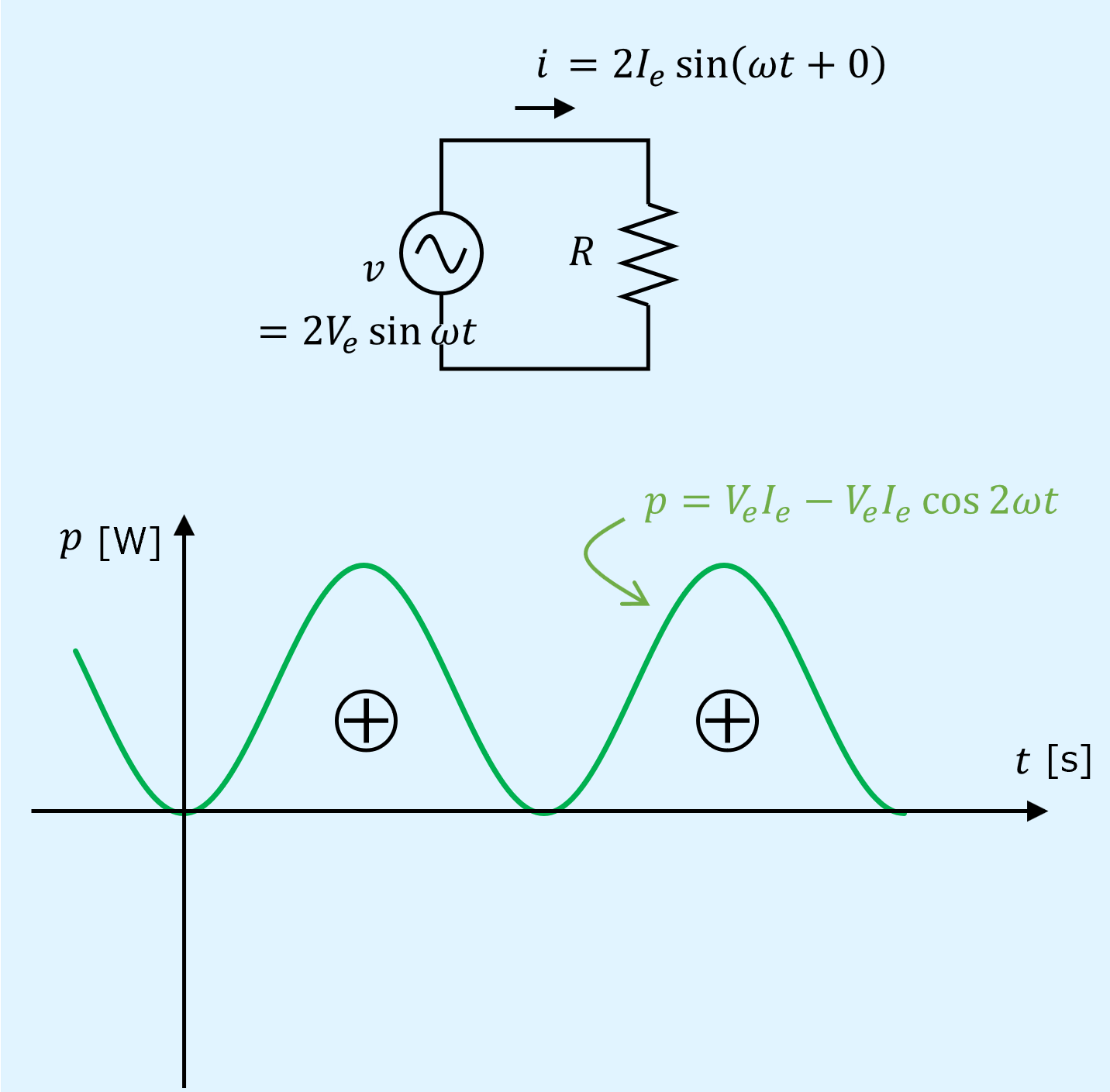
最初に、無効電力が0となる、交流電源に抵抗のみを接続した回路と、そのときの電力の瞬時値\(p\)の波形を以下に示します。
\(p\)は時間変化しますが、0を下回ることはありません。
すなわち、抵抗は電源から電力を一方的に受け取るだけのものであると言えます。
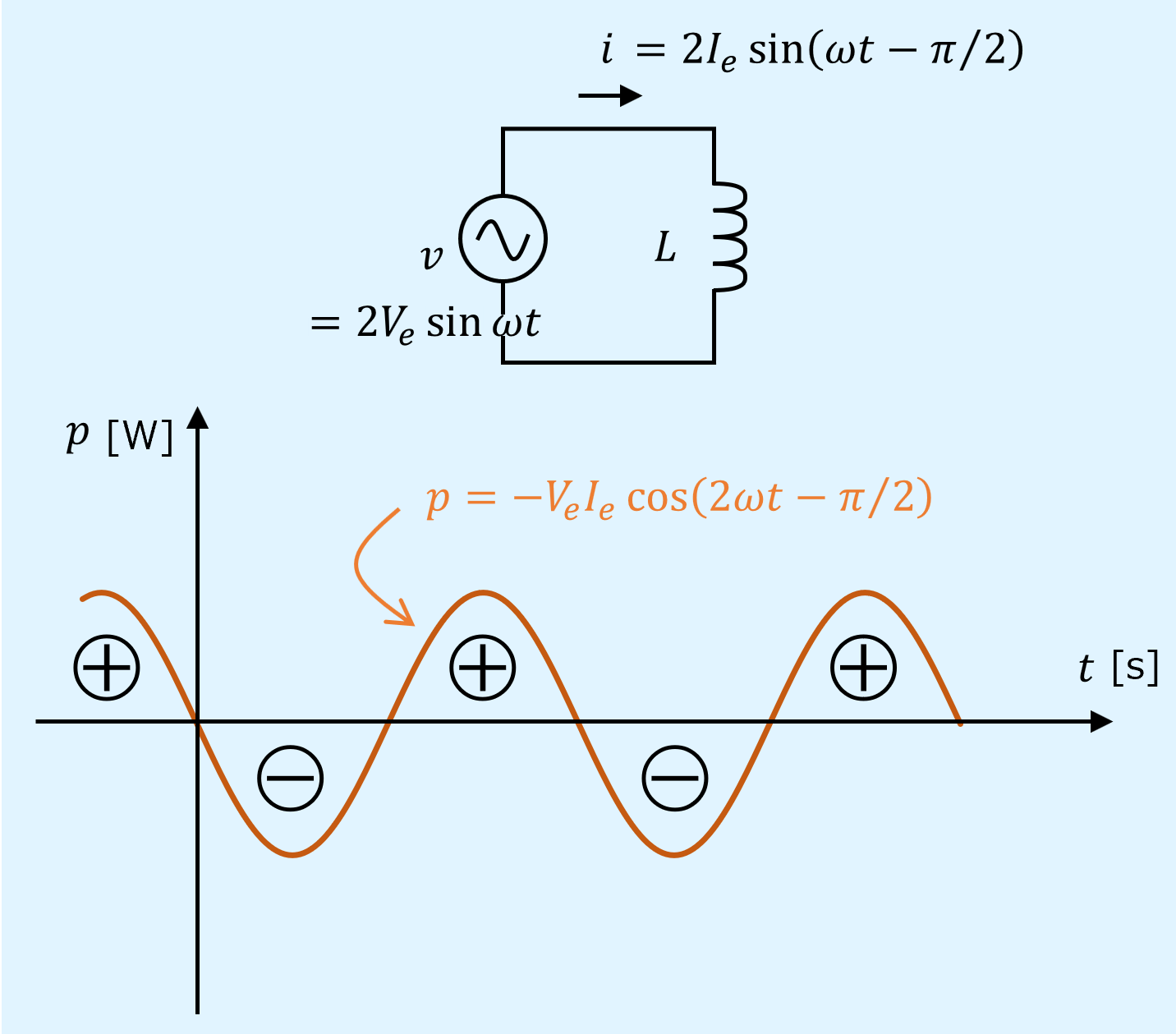
次に、交流電源にインダクタのみを接続した回路と、そのときの\(p\)の波形を以下に示します。
このとき位相差は\(\varphi=-\pi/2\)となります。
\(p\)は0を中心に±で変動します。
ここで、+側は先の抵抗と同じく、電源から電力を受け取っている状態です。
では-側は何を意味しているのでしょうか。
これはインダクタが受け取った電力を電源に返す、すなわち放電している状態であることを意味します。
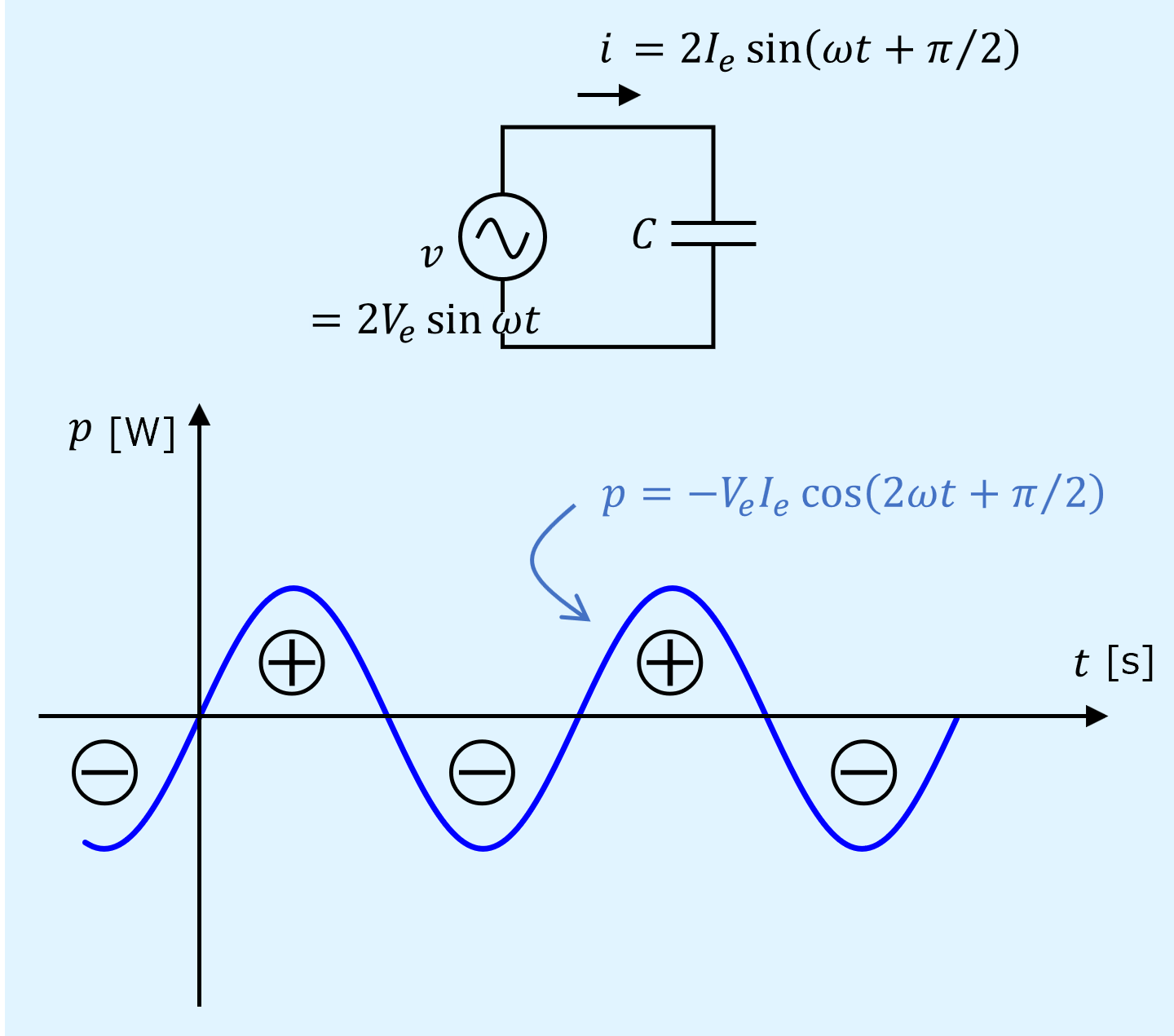
また、交流電源にキャパシタンスのみ接続した回路と、そのときの\(p\)の波形も以下に示します。
このとき位相差は\(\varphi=\pi/2\)となります。
インダクタの時と同様に、0を中心に±で変動しており、電源とキャパシタンスの間で電力の受け渡しをしているだけであり、消費していないことが分かります。
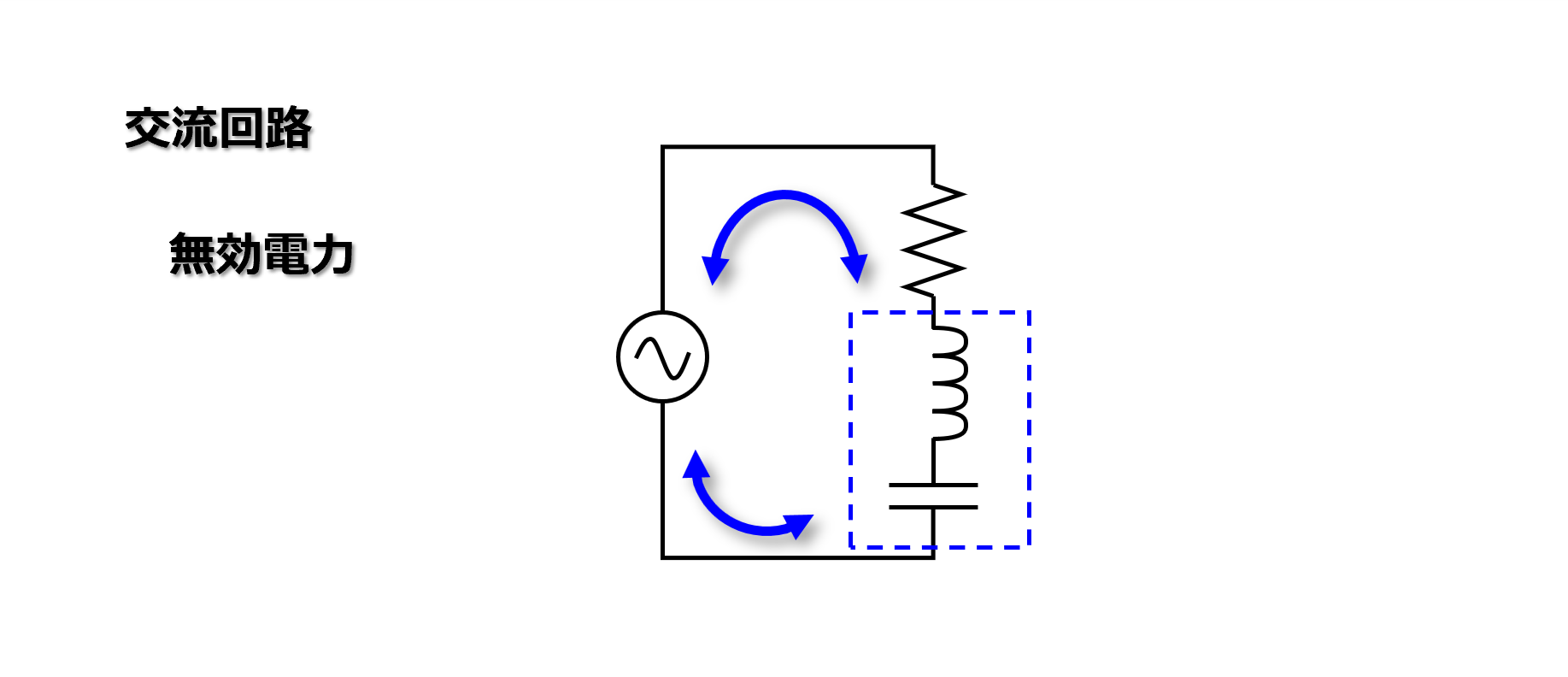
このように、インダクタ、キャパシタのリアクタンスは、電力を消費せずに電源との間で電力のキャッチボールをしているだけの存在です。
ではこのキャッチボールされている電力が無効電力でしょうか。
答えは否です。
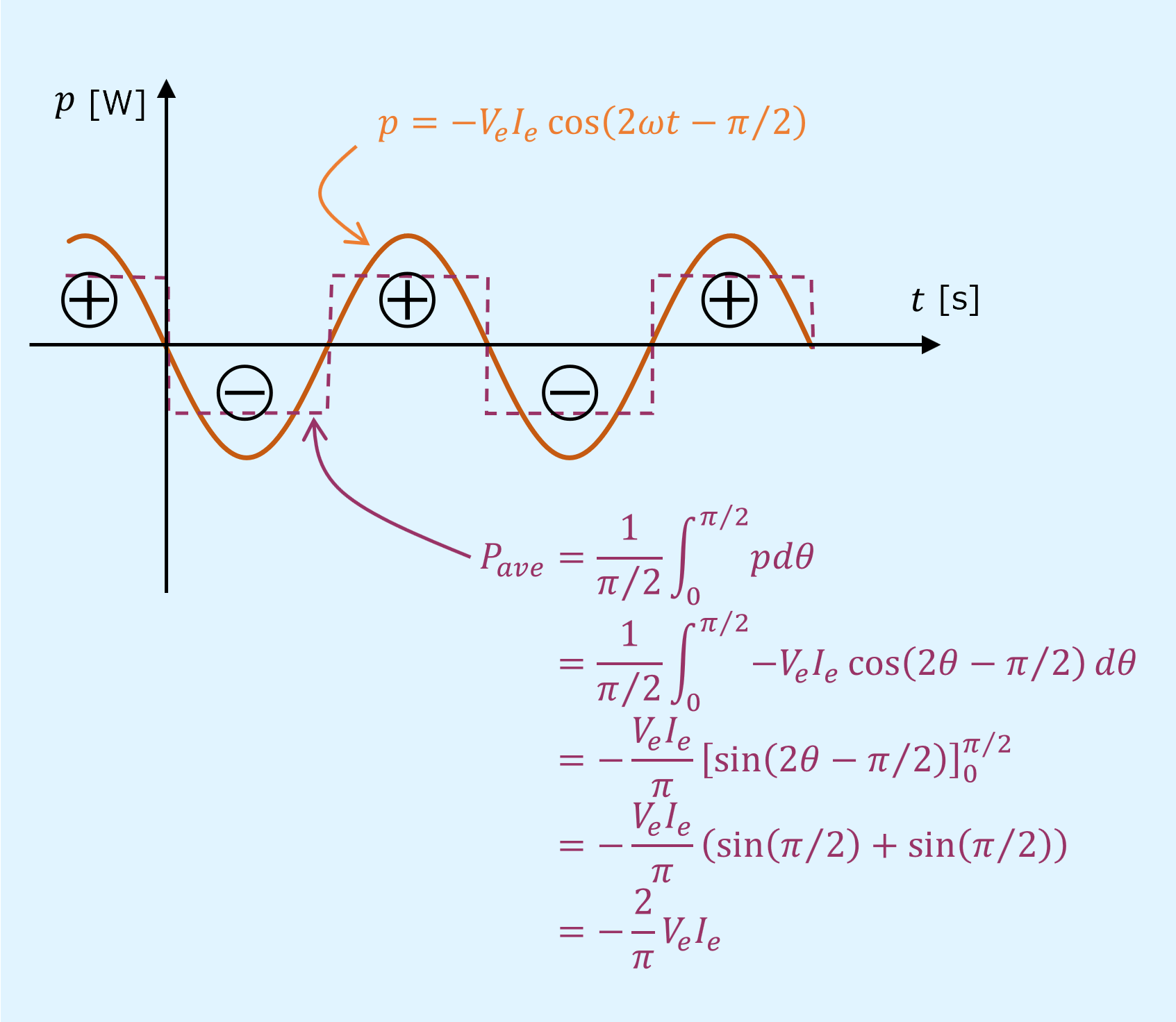
以下のように受け渡しの片方のみ積分すると、キャッチボールしている電力の大きさは\(2V_eI_e/\pi\)となります。
となると、結局無効電力とは何でしょうか。
無効電力とは、この電力のキャッチボールをするために、電源に必要とされる出力のことを指します。
負荷側の話ではなく、電源側の話にいつの間にかなっているので、混乱が生じます。
無効電力は電源側に求められる出力のこと
リアクタンスで電力が消費されなくても、電源は設定された電圧で、必要となる電流を流さないといけません。
例えば、電源電圧が\(V_e=100\)[V]で、負荷がリアクタンス\(X=5\)[Ω]の場合、電力が消費されなくても\(I_e=20\)[A]の電流を流さなければいけません。
すなわち、無駄な電力のキャッチボールを行うために電源に求められる出力が無効電力です。
以下のように式展開していくと、有効電力\(P_a\)と無効電力\(P_r\)の2乗和平方を電圧で割って得られる電流を電源は出力する必要があります。
その他
電気回路全般については以下をご覧下さい。


コメント