この記事では電気回路の一種であるRLC直列回路の過渡現象について取り扱います。
負荷と電源の間にあるスイッチをONにした後に生じる過渡現象は、電流と電圧の時間変化で表されます。
各種法則と関係式、初期条件から電流と電圧の式を導き出しますが、式を立てたり、変形したりすることが苦手な人でも分かりやすいよう順序立てて詳細に説明を行います。
目次
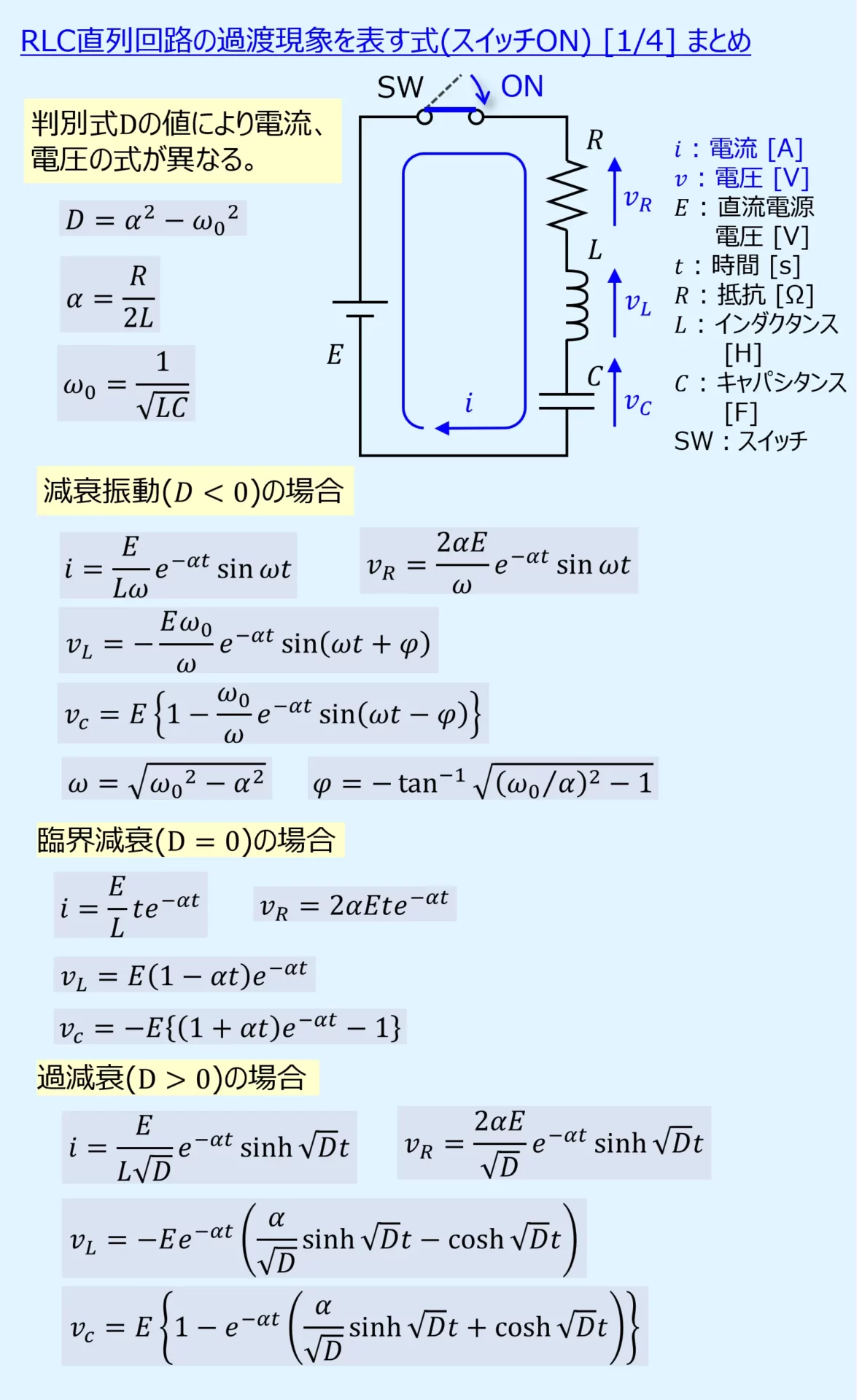
【まとめ】RLC直列回路の過渡現象を表す式(スイッチON) [1/4]
最初にまとめです。
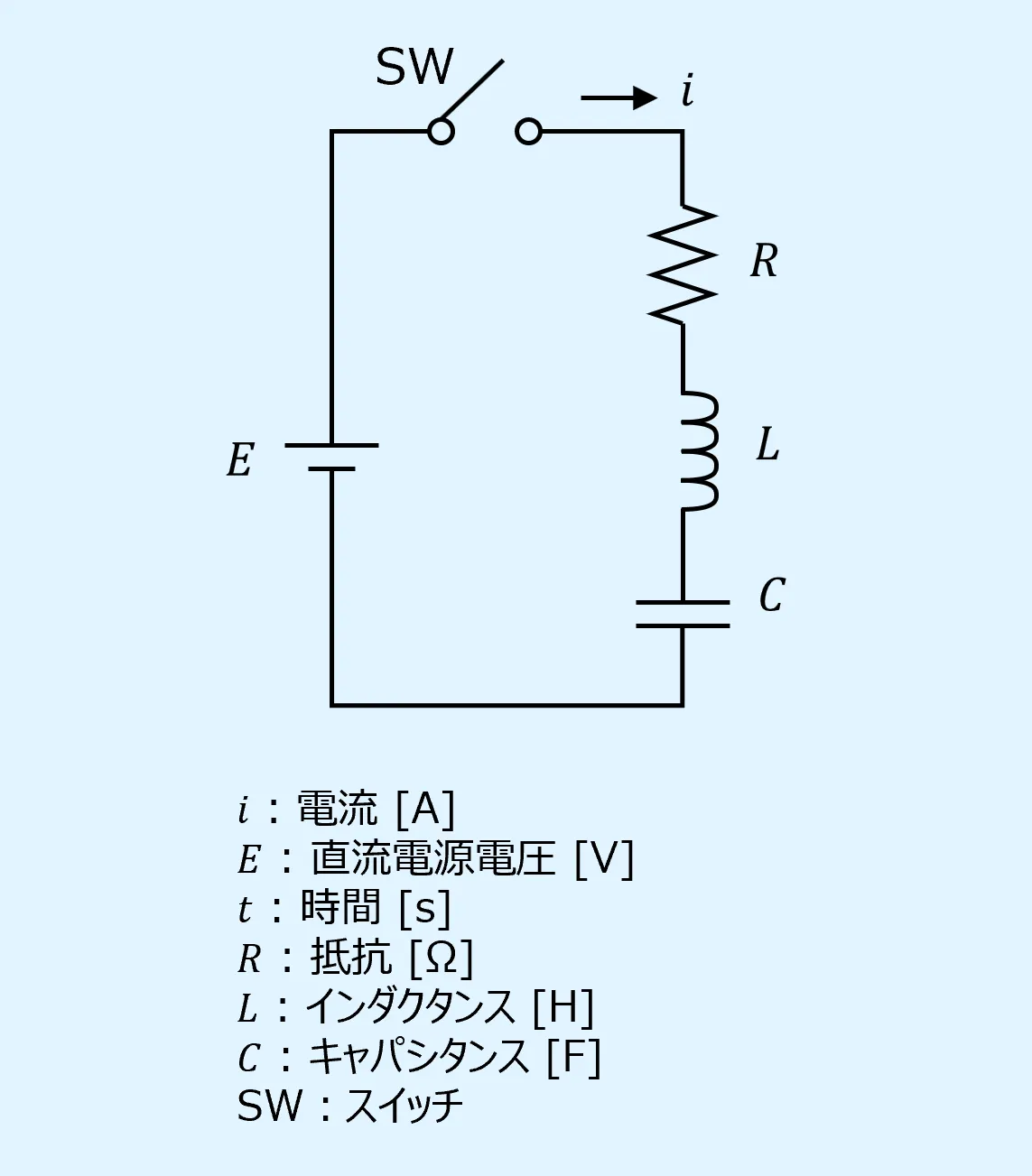
対象とする回路
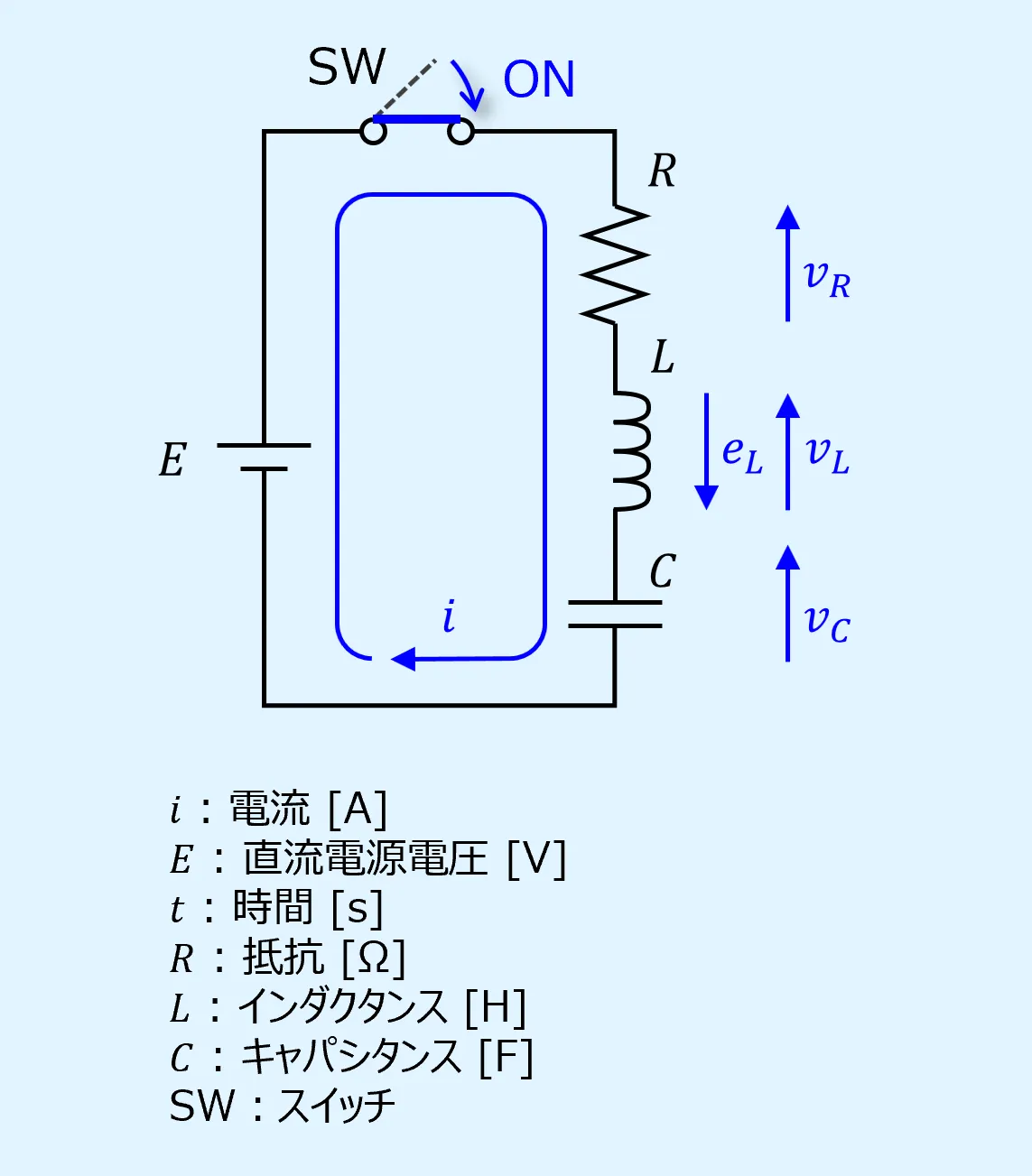
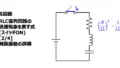
本記事で対象とする回路はRLC直列回路で、抵抗RとインダクタL、キャパシタCの直列接続からなる負荷に直流電源を接続したものです。
RLCの負荷と電源の間にはスイッチSWを設けています。
このスイッチをONに切り替えることで生じる過渡現象について、以降で電流\(i\)と電圧\(v\)の式を導出します。
過渡現象を表す式の求め方
以下の順番で過渡現象を表す\(i\),\(v\)の式を導出します。
(1)初期状態の条件を求める。
(2)スイッチをONにした回路で微分方程式を立てる。
(3)解を仮定して微分方程式を解く。
(4)判別式の範囲ごとに解を再仮定して未定定数を求める。
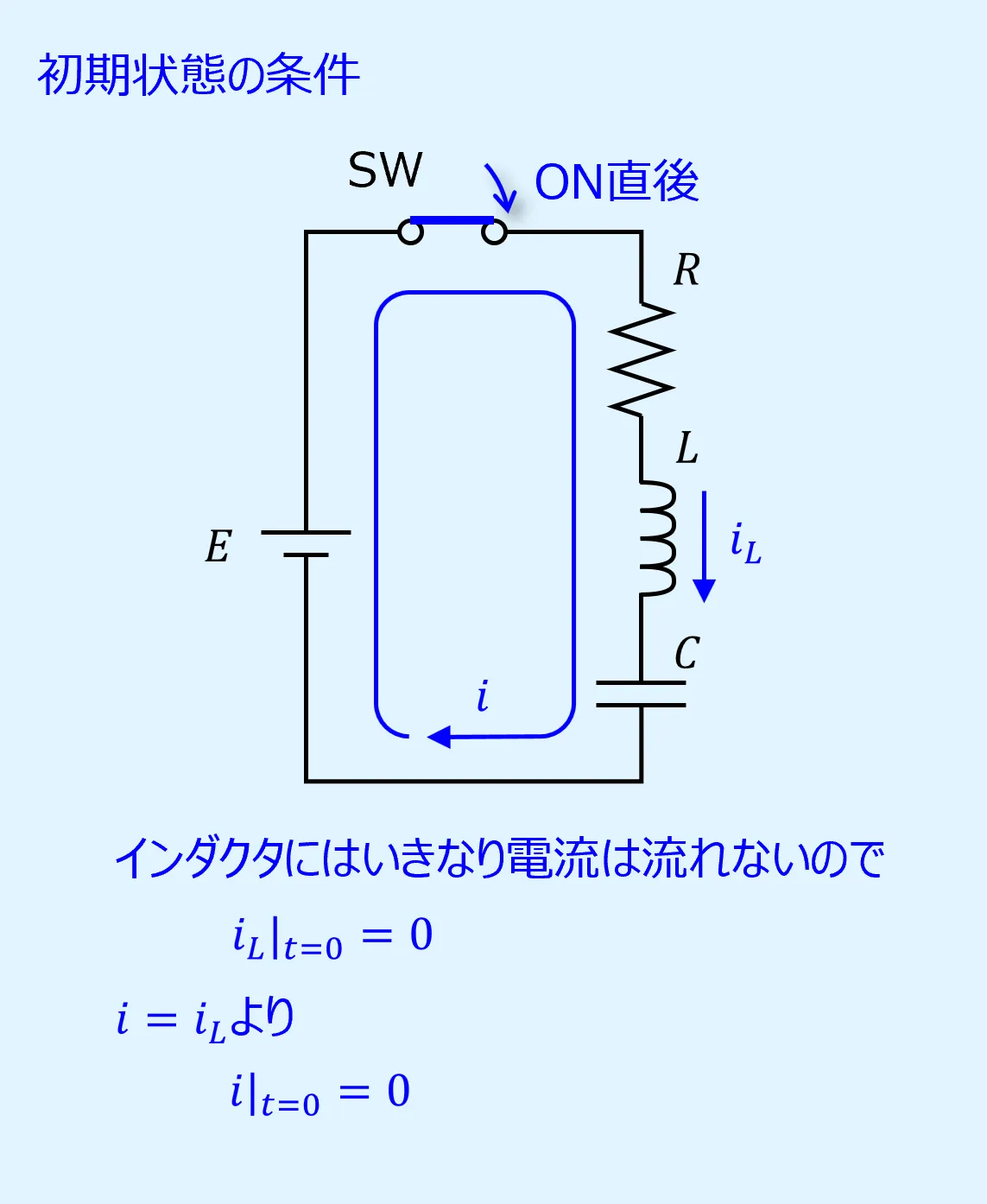
(1)初期状態の条件を求める
いま、RLC直列回路のスイッチがOFFになってから十分に時間が経っているとします。
そこからスイッチをONにした直後の状態を考えます。
スイッチがONになっても、インダクタにはいきなり電流は流れません。
そのためONになった直後の初期状態では\(i=0\)となります。
これがRLC直列回路のスイッチをONにしたときの初期状態の条件です。
(2)スイッチをONにした回路で微分方程式を立てる
RLC直列回路のスイッチをONにすると過渡現象が起きます。
このときの\(i\)と\(v\)の向きは以下とします。
上記のRLC直列回路に関して、キルヒホッフの第2法則、オームの法則、誘導起電力の式、電荷とキャパシタンスの関係式から、以下が得られます。
以上よりRLC直列回路に流れる\(i\)に関する微分方程式を立てることができます。
(3)解を仮定して微分方程式を解く
次に過渡現象の解とその微分を以下のように仮定します。
これをRLC直列回路の微分方程式に代入すると、未定定数\(B\)が得られます。
ここで、\(\alpha\)、\({\omega}_0\)、\(D\)を次のように定義すると、\(B\)は以下となります。
(4)判別式の範囲ごとに解を再仮定して未定定数を求める
\(D\)は判別式となっており、\(D<0\)、\(D=0\)、\(D>0\)のいずれとなるかで解の形が変わります。
解の形が異なるということは、過渡現象の様相も変わるということです。
に\(D<0\)の場合は振動が生じますので注意をしましょう。
ここからの手順ですが、判別式の範囲ごとに解を仮定し直し、初期条件\(i=0\)を用いて未定定数Aを求めます。
以降では導出結果の式のみ提示し、導出過程については別の記事とします。
興味のある方はそちらもご覧下さい。
(4-1) \(D<0\)の場合:減衰振動
\(D<0\)となる場合は減衰振動と呼ばれます。
式中にsin項とexp項が現れるためで、スイッチをONにするとRLC直列回路は振動しながら減衰していきます。
(4-2) \(D=0\)の場合:臨界減衰
\(D=0\)となる場合は臨界減衰と呼ばれます。
\(D\)が0以上になると振動が生じることなく定常状態へ収束します。
\(D=0\)は振動する、しないの境界点なので「臨界」と呼ばれる訳ですね。
臨界減衰の状況下でRLC直列回路は最も速く定常状態へ収束します。
(4-3) \(D>0\)の場合:過減衰
\(D>0\)となる場合は過減衰と呼ばれます。
\(D\)の値が大きい程、定常状態への収束に時間を要する過渡現象となります。
おわりに
以上がRLC直列回路のスイッチをONにしたときに生じる過渡現象を表す電流と電圧の式となります。
判別式Dの値により式の形が変わることがポイントです。
本記事がみなさんの理解の一助になれば幸いです。
その他
電気回路全般については以下をご覧下さい。




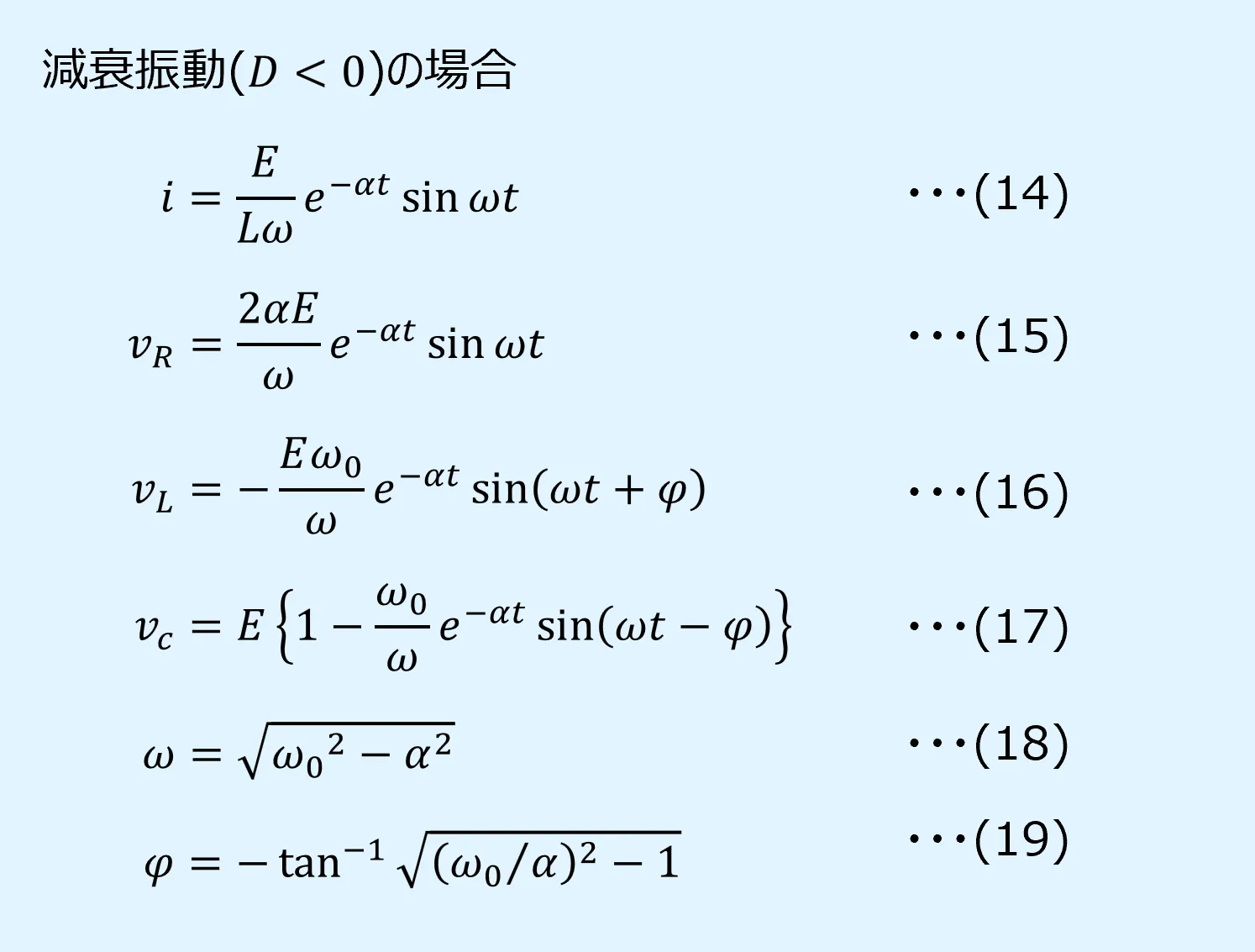

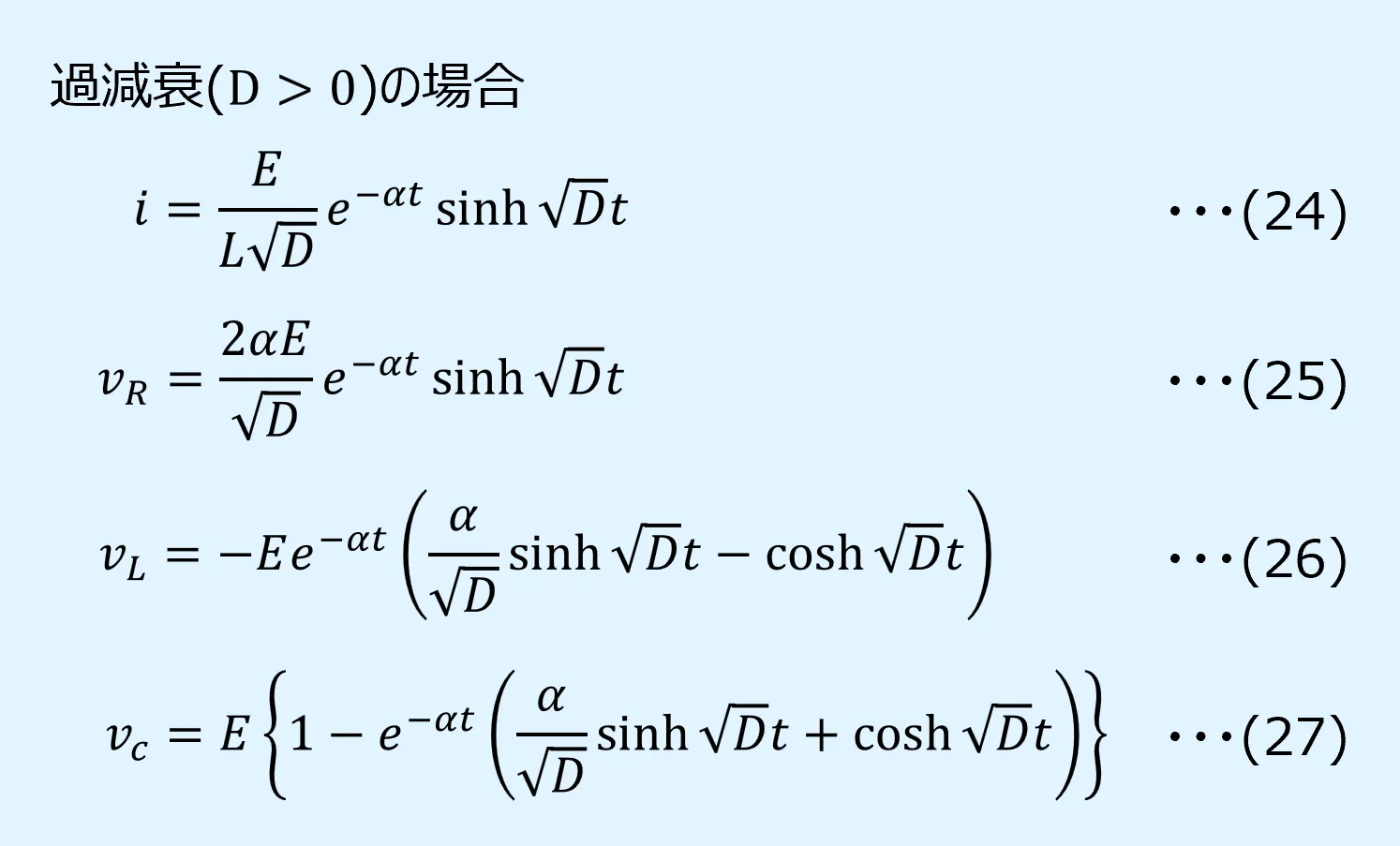

コメント