この記事では電気回路で生じる反共振という事象ついて説明をします。
RLC並列回路のアドミタンスと電流の振幅、位相の周波数特性との関係も含めています。
目次
【まとめ】回路の反共振
RLC並列回路と電流
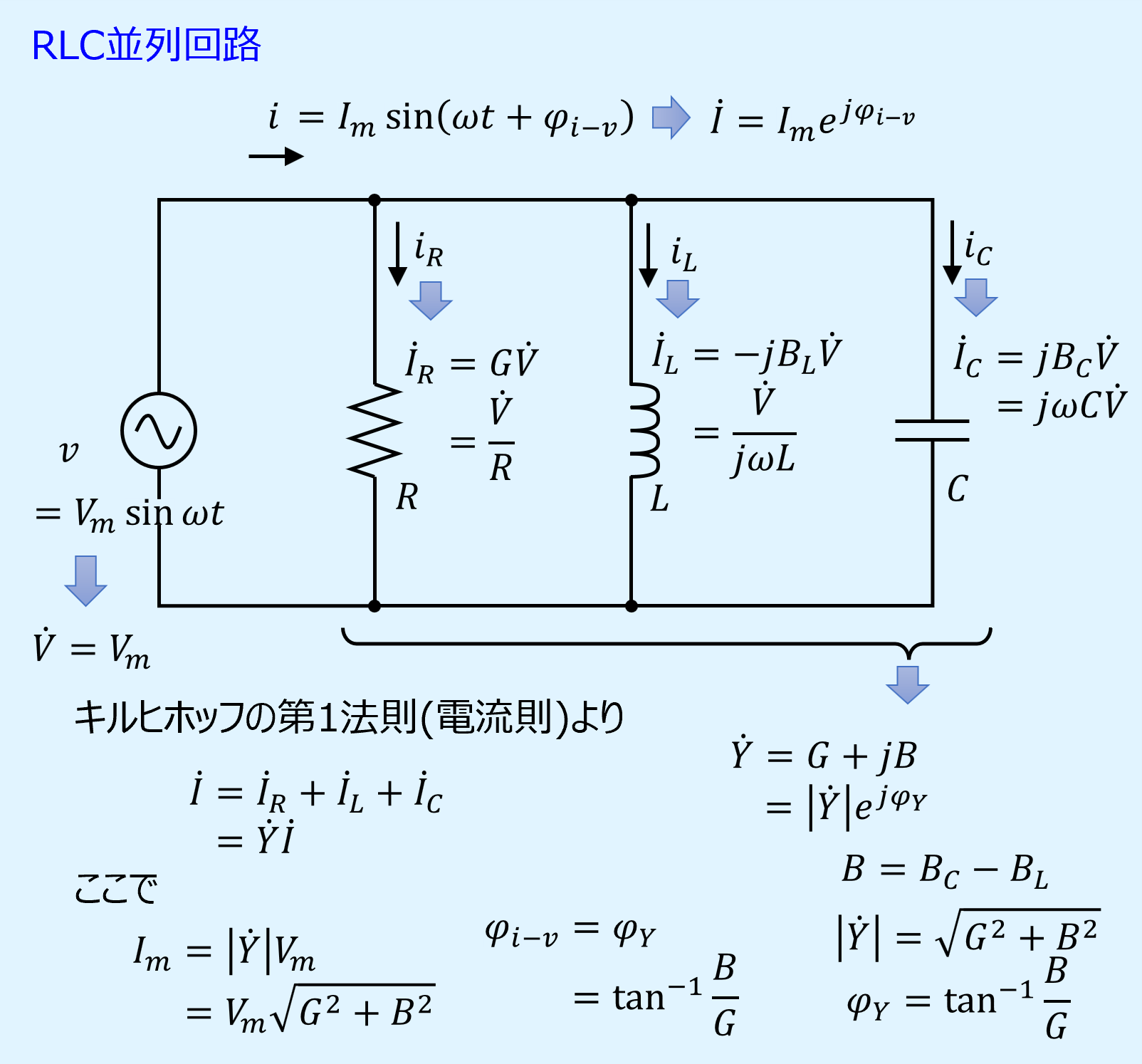
以下にRLC並列回路と電流の関係を示します。
ここで、交流での電流の流れやすさを表すサセプタンス\(B_L\)と\(B_C\)は周波数によって値が変化します。
そのため、サセプタンス\(B\)とコンダクタンス\(G\)を合成したアドミタンス\(\dot{Y}\)、及び電圧\(\dot{V}\)とアドミタンス\(\dot{Y}\)を掛け合わせて得られる電流\(\dot{I}\)の最大振幅\(I_m\)、電圧と電流の位相差\(\varphi_{i-v})も周波数によって値が変わります。
本記事ではアドミタンスの大きさ\(|\dot{Z}|\)と電流の最大振幅\(I_m\)、電圧と電流の位相差\(\varphi_{i-v})が周波数によってどのように変化するのか、また変化させる途中で起きる事象について説明します。
コンダクタンスとサセプタンスの周波数特性
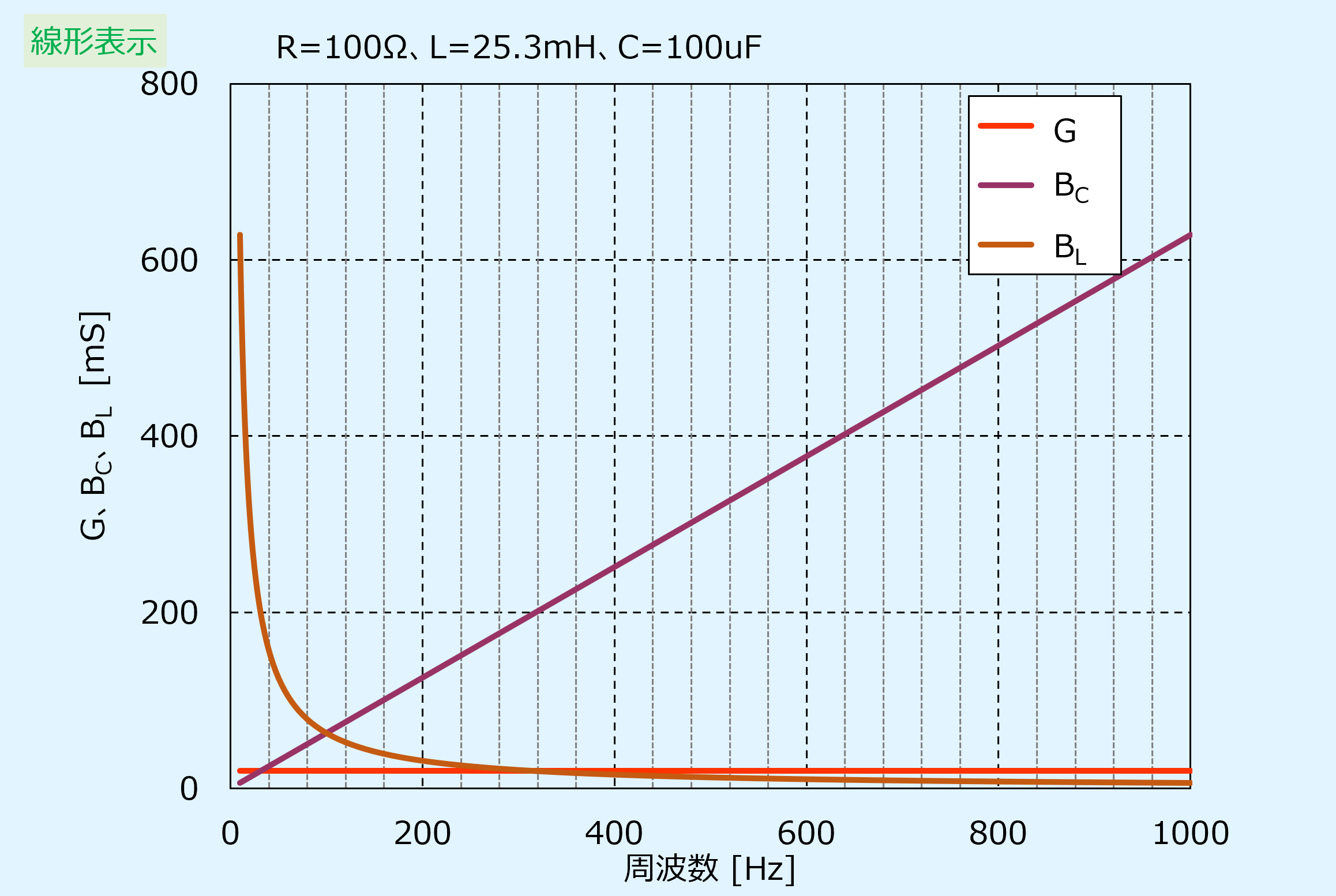
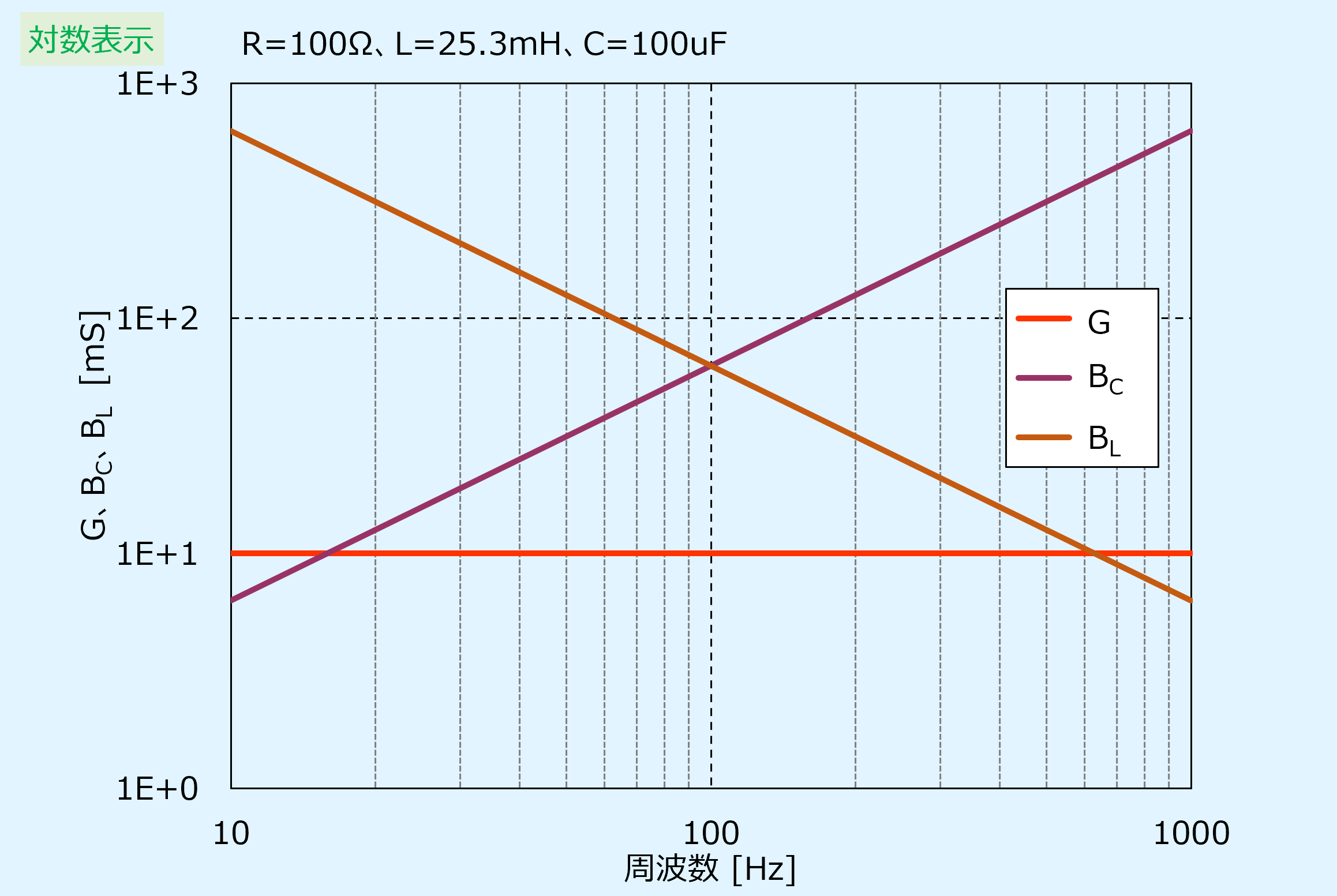
最初にコンダクタンス\(G\)、誘導性サセプタンス\(B_L\)、容量性サセプタンス\(B_C\)について、周波数を変化させたときにどうなるのかを以下に示します。
横軸は周波数[Hz]で、縦軸に\(G\)、 \(B_L\)、 \(B_C\)[mS]の値を示しています。
条件としては、\(R=100\)Ω、\(L=25.3\)mH、\(C=100\)uFの場合です。
コンダクタンス\(G\)は周波数特性を持たないので、周波数によらず一定です。
誘導性サセプタンス\(B_L\)は周波数が低いと大きく、周波数に反比例して小さくなります。
容量性サセプタンス\(B_C\)は周波数が低いと小さく、周波数に比例して大きくなります。
先のグラフを縦軸、横軸共に対数表示にしたものを以下に示します。
こちらの方が見慣れている人が多いかもしれません。
対数表示の方が「特性」という観点では線形表示より全体像をつかみやすくなります。
アドミタンスと電流の周波数特性
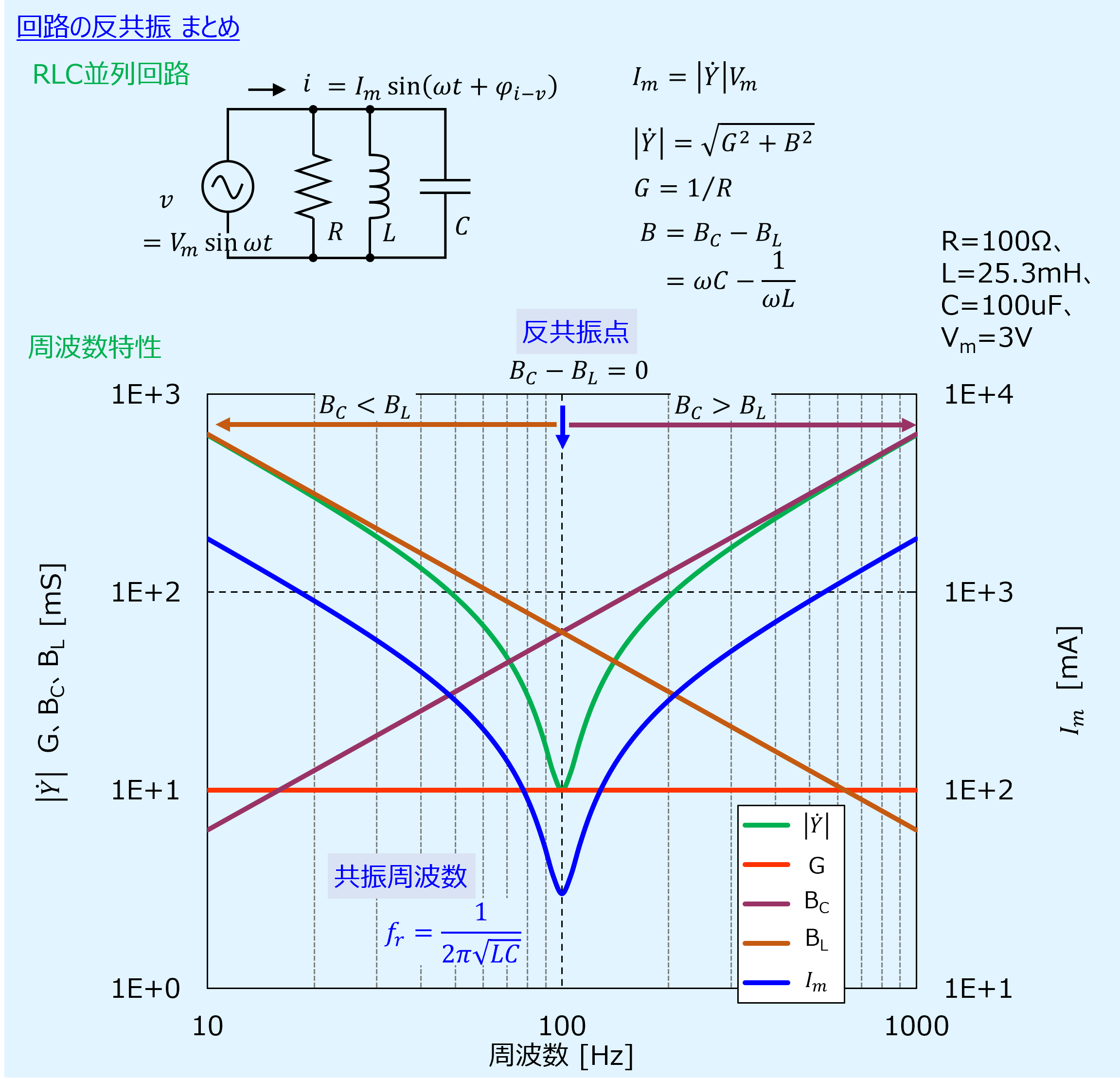
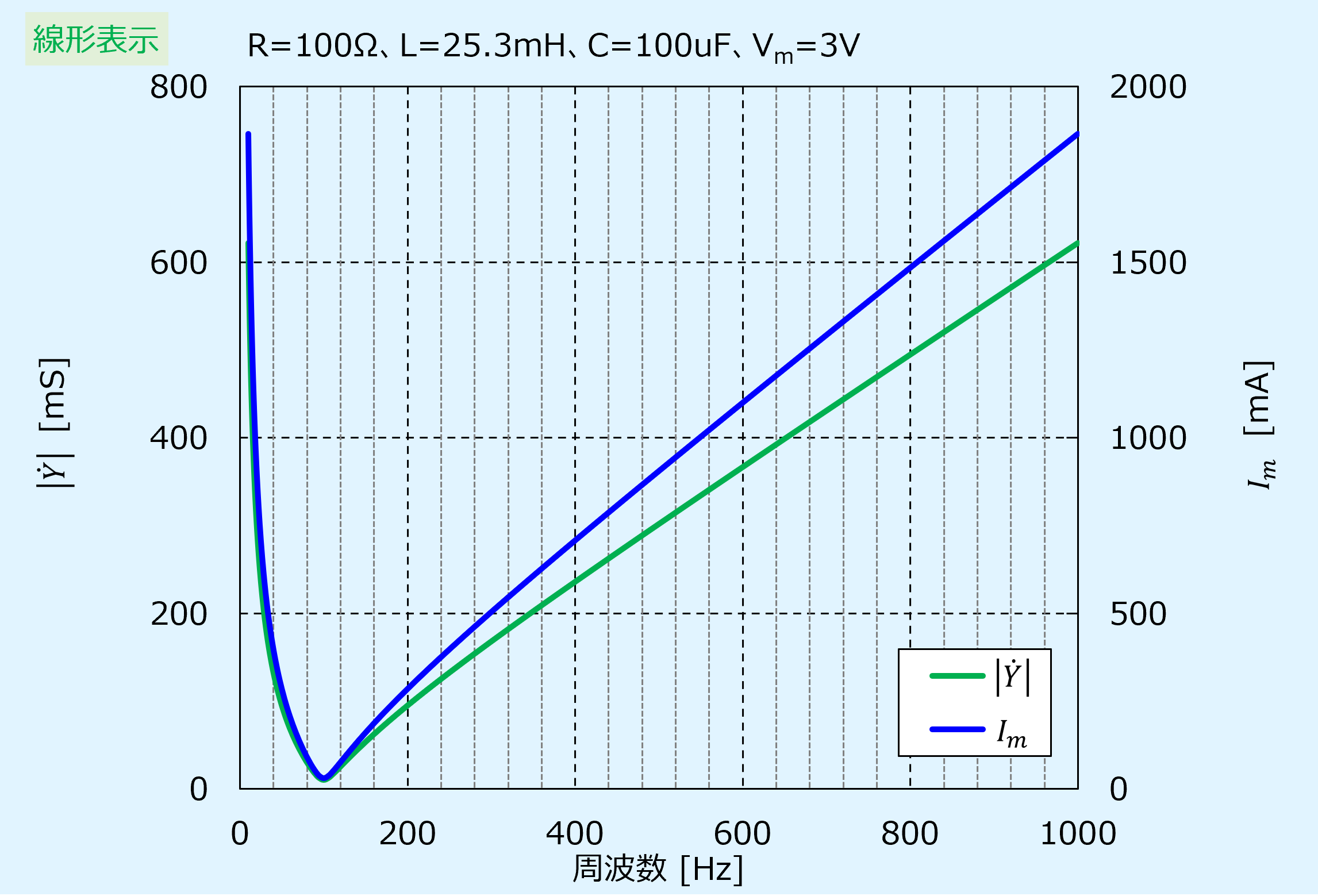
次にアドミタンスの大きさ\(|\dot{Y}|\)と電流の最大振幅\(I_m\)の周波数特性を示します。
電圧の最大振幅\(V_m\)は3Vとしています。
また、左側の縦軸が\(|\dot{Y}|\)[mS]、右側の縦軸が\(I_m\)[mA]となっています。
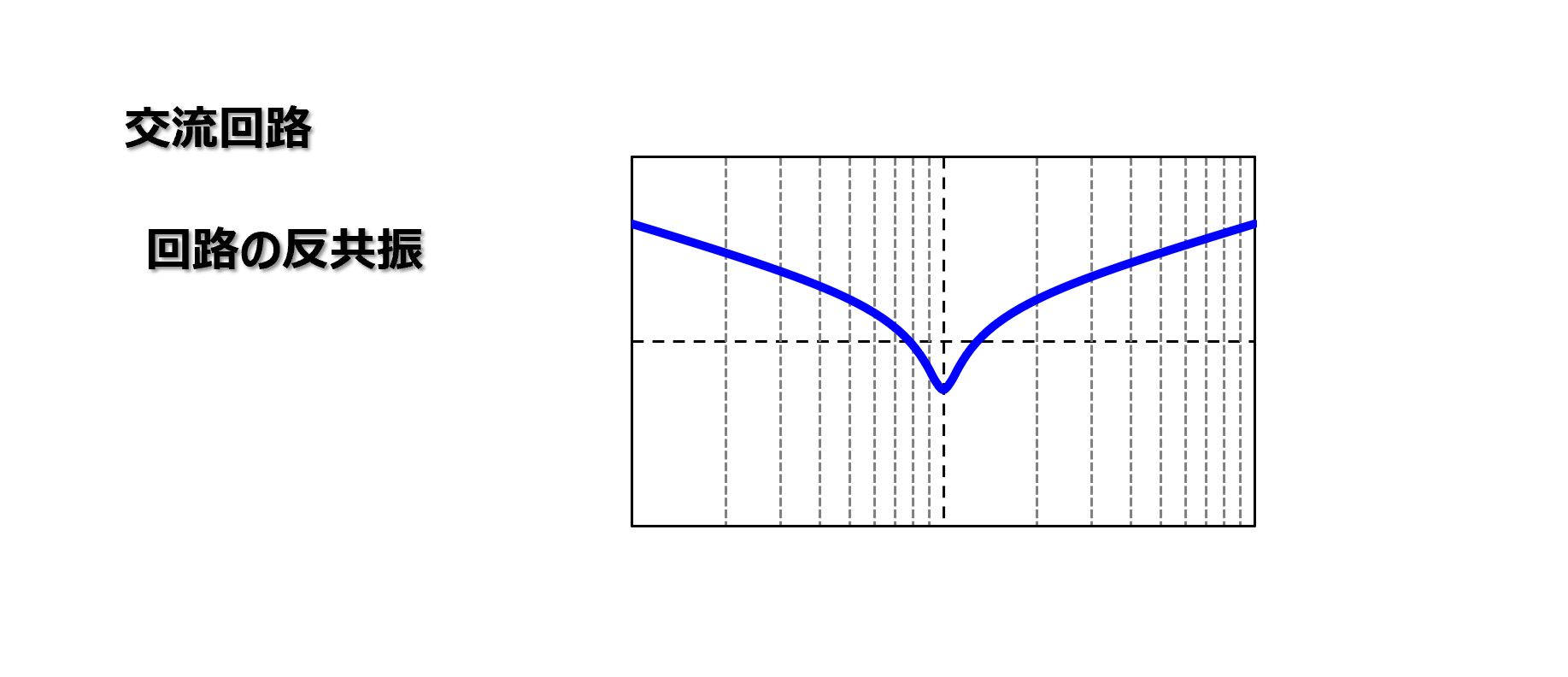
コンダクタンス、誘導性/容量性サセプタンスを合成したアドミタンスの周波数特性はV字の形となります。
周波数が低い領域では誘導性サセプタンスの影響が強く出てアドミタンスは大きく、周波数が高くなるにつれて小さくなります。
そして、ある周波数で誘導性/容量性サセプタンスが打ち消し合いコンダクタンスのみとなる最小値を迎えます。
その後の周波数が高い領域では容量性サセプタンスの影響が強く出てアドミタンスは大きくなっていきます。
電流は電圧とアドミタンスを掛け合わせたものですので、電圧が一定の場合、電流はアドミタンスと同じV字の周波数特性となります。
電流は低域で大きく、周波数が高くなるに従い小さくなり、ある点で最小値を迎え、その後は周波数が高くなるに従い大きくなります。
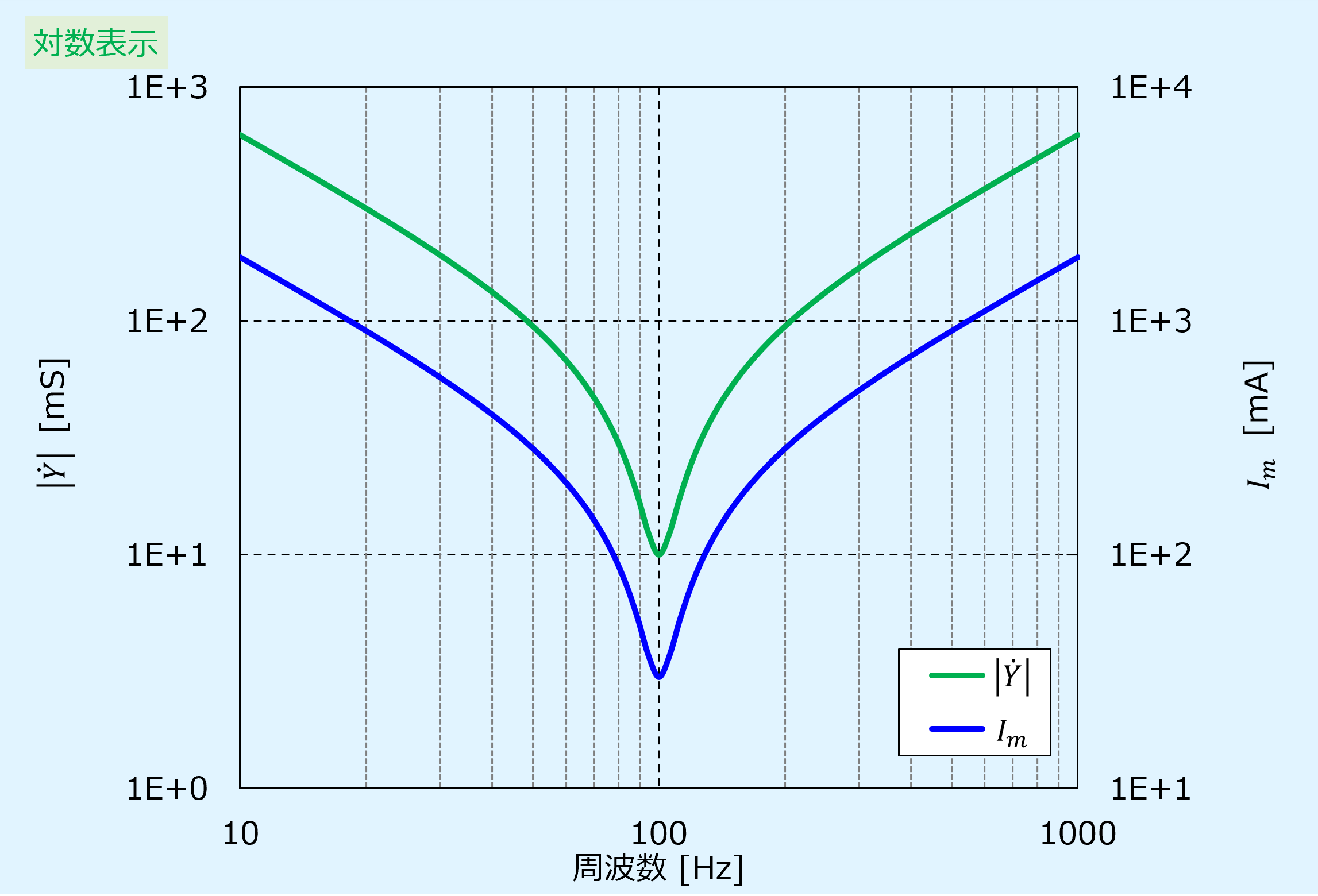
先のグラフを縦軸、横軸共に対数表示にしたものを以下に示します。
対数表示だと最小値が鋭いピークになり見やすくなります。
インピーダンスの周波数特性
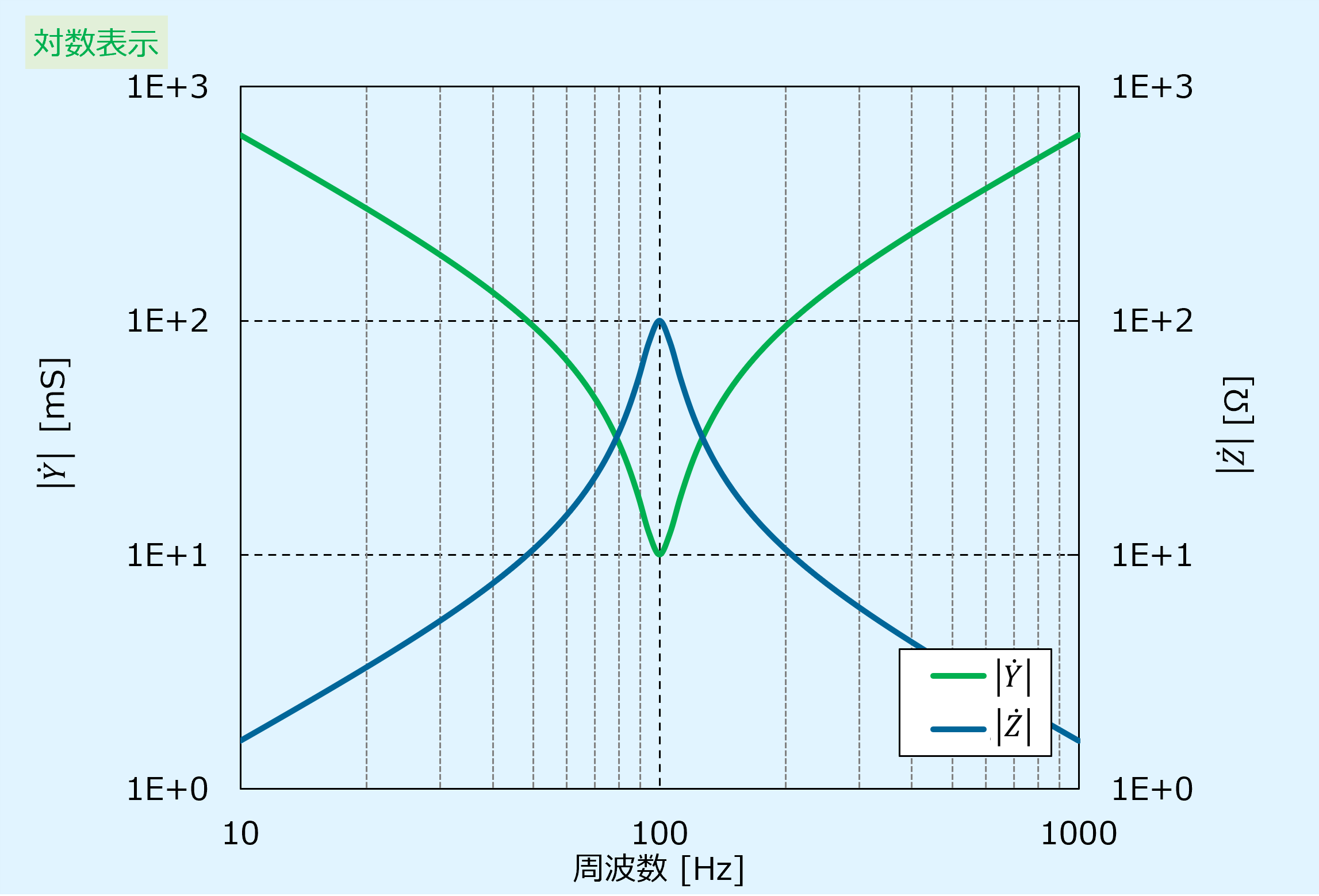
アドミタンスと逆数の関係にあるインピーダンスの周波数特性は以下となります。
右側の縦軸に\(|\dot{Z}|\)[Ω]を示しています。
アドミタンスとは逆の関係で、裾が広い山の周波数特性となり、アドミタンスが最小値となる点でインピーダンスは最大値となります。
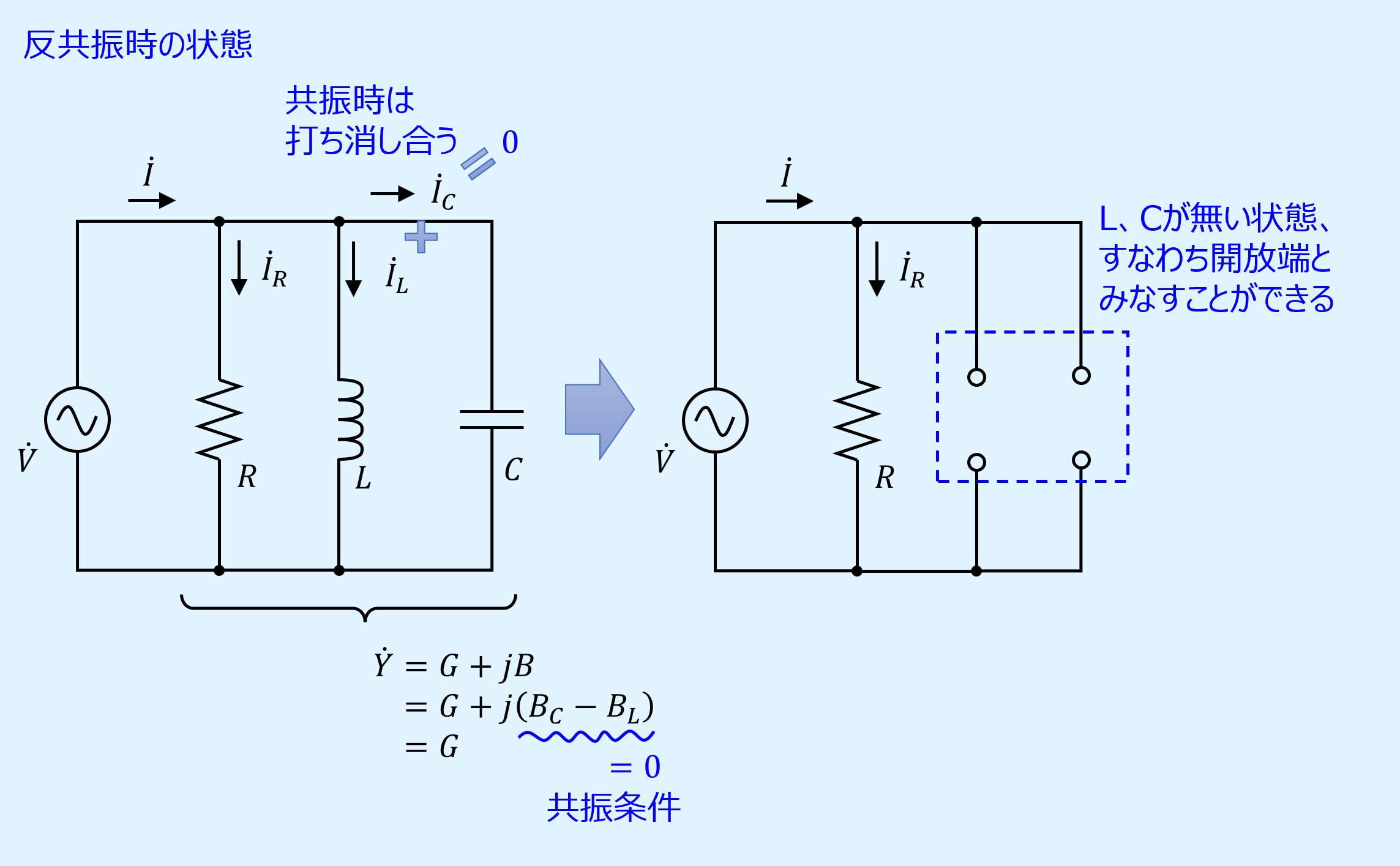
反共振
RLC並列回路の周波数特性で、電流が最小となる点を反共振(antiresonance)、あるいは並列共振(parallel resonance)、もしくは直列回路と同様に共振いいます。
また、LCが並列に接続された回路のことを並列共振回路と呼びます。
反共振点ではインダクタンス\(L\)とキャパシタンス\(C\)に生じる電流が互いに打ち消し合っており、実質的に\(L\)、\(C\)が無い状態、すなわち開放端状態にあるとみなすことができます。
共振となる条件、及び共振周波数は以下の通りです。
位相の周波数特性
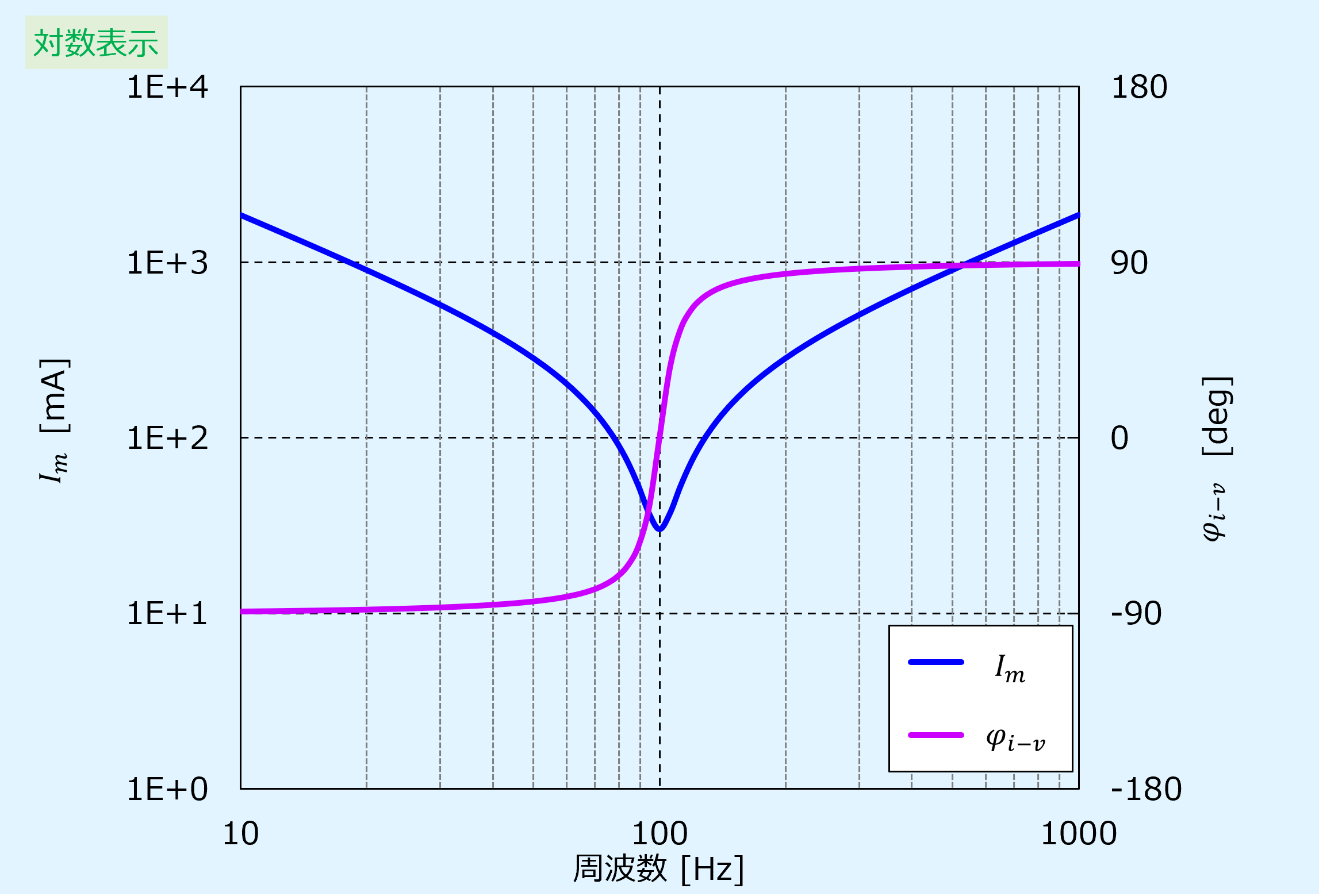
最後に電圧と電流の位相差\(\varphi_{i-v}\)の周波数特性を以下に示します。
比較として、電流の最大振幅\(I_m\)も合わせて表示しています。
周波数が低い領域では誘導性が優勢であるため位相が遅れ、高い領域では容量性が優勢のため位相が進みます。
そして、反共振点で電流と電圧の位相差は無くなり同相となります。
その他
電気回路全般については以下をご覧下さい。

コメント