この記事では電気回路のインピーダンスについて説明をします。
インピーダンスとその要素から等価回路とベクトル図、オームの法則との関係までを扱います。
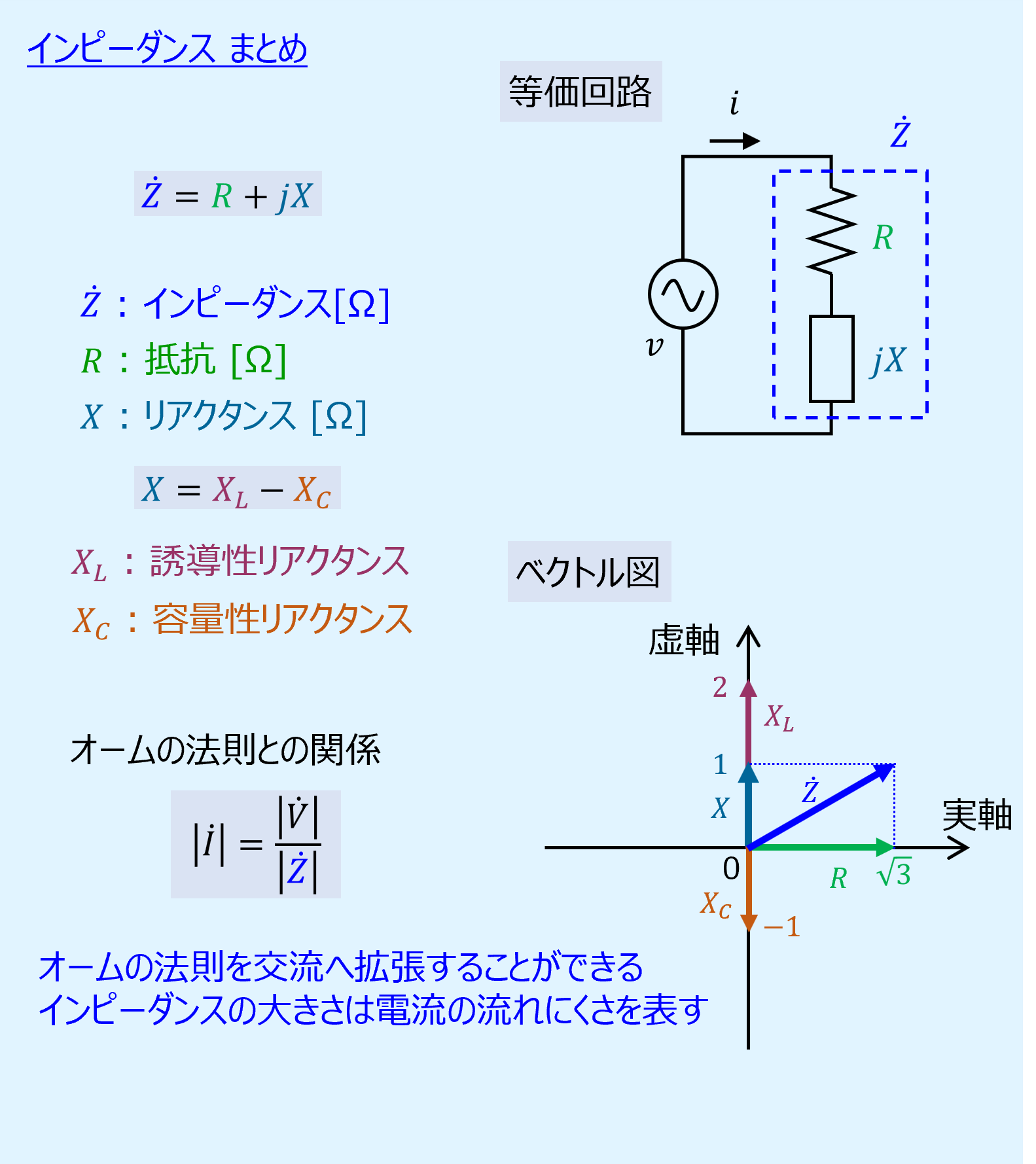
【まとめ】インピーダンス
最初にまとめです。
リアクタンス
交流回路では、抵抗と似たような働きをする、すなわち電流が流れるのを妨げるものとして、リアクタンス(reactance)が存在します。
リアクタンスには誘導性と容量性があり、両者の差が合成リアクタンス(または単にリアクタンスと呼ぶ)となります。
回路には誘導性、容量性のどちらかしかないわけではなく、両方とも存在しており、誘導性の方が大きければリアクタンスは正に、容量性の方が多きければリアクタンスは負となります。
インピーダンス
リアクタンスを抵抗と合わせて複素数として表現したものをインピーダンス(impedance)と呼びます。
抵抗\(R\)を実数部、リアクタンス\(X\)を虚数部とします。
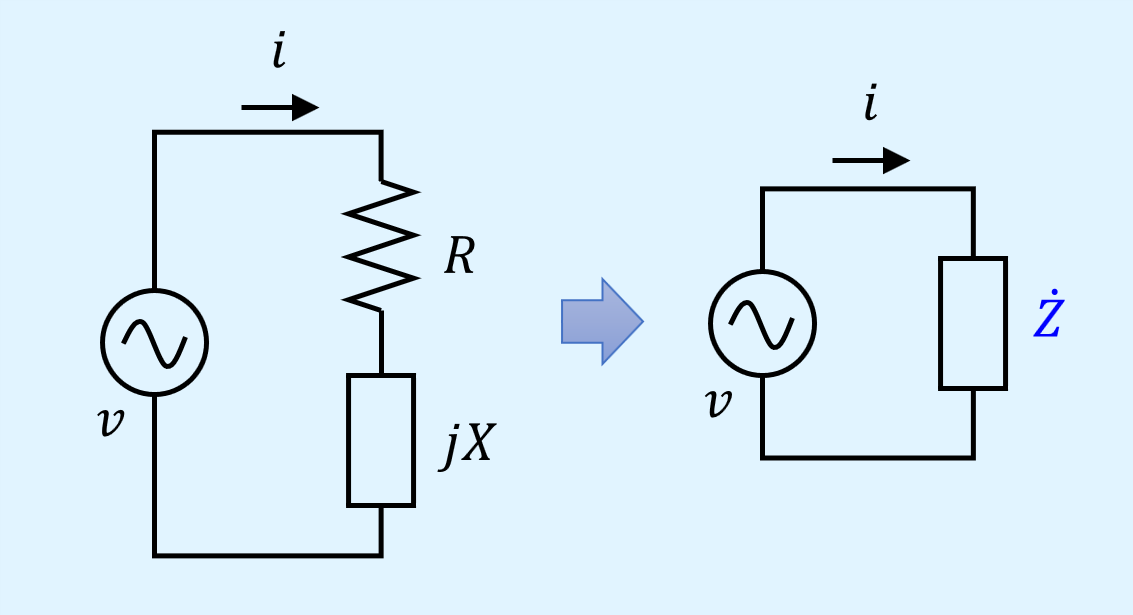
等価回路
インピーダンス\(\dot{Z}\)の等価回路は抵抗\(R\)とリアクタンス\(X\)の直列接続で表されます。
ベクトル図
インピーダンスは複素平面上でベクトルとして表現が可能です。
抵抗\(R\)は実軸成分で、リアクタンス\(X\)は虚軸成分となります。
リアクタンス\(X\)は正方向の誘導性リアクタンス\(X_C\)と負方向の容量性リアクタンス\(X_L\)の差として表されます。
オームの法則との関係
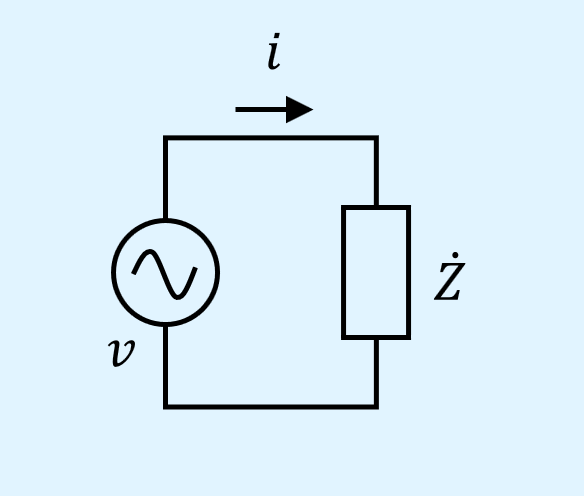
次にインピーダンスと電圧、電流の関係を確認します。
交流電圧源にインピーダンスを接続しただけの簡単な回路を以下に示します。
上記の回路で、電圧と電流の瞬時値\(v\)、\(i\)は以下となります。
ここで、\(V_m\)、\(I_m\)は最大振幅、\(\varphi_v\)\(\varphi_i\)は位相を表しています。
上記の電圧、電流の瞬時値をフェーザを使って極座標表示すると以下となります。
また、電圧源に接続しているインピーダンスを極座標表示すると以下となります。
インピーダンスの大きさ\(|\dot{Z}|\)ですが、これがインピーダンスの値として通常用いられ、50Ωや75Ωなど示されます。
電流のフェーザは、電圧のフェーザをインピーダンスで割ることで求まります。
逆に、電圧のフェーザは電流のフェーザとインピーダンスを掛け合わせることで求まります。
ここで、電圧、電流の位相\(\varphi_v\)\(\varphi_i\)とインピーダンスの位相\(\varphi_z\)には以下の関係があります。
すなわち、電流の位相は電圧の位相よりインピーダンスの位相分だけ進み、電圧の位相は電流の位相よりインピーダンスの位相分だけ遅れることになります。
また、電圧、電流、インピーダンスの大きさには以下の関係が成立しています。
これはオームの法則で抵抗\(R\)をインピーダンスに置き換えたものであり、オームの法則が交流にも拡張可能であることを意味しています。
電圧、電流の大きさは最大振幅に対応していますので、次式のように書き換えることができます。
実効値\(V_e\)、\(I_e\)について書き直すと以下となり、オームの法則が成り立ちます。






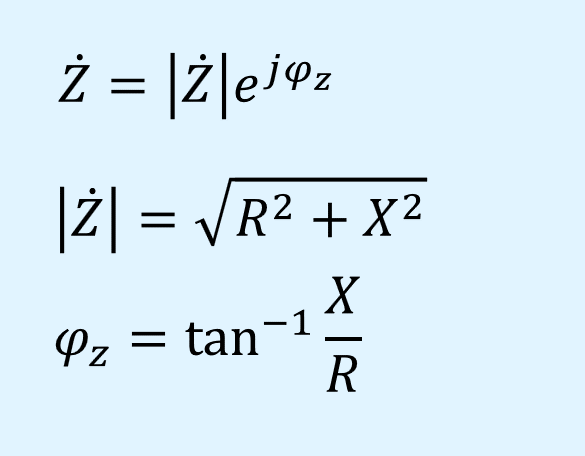
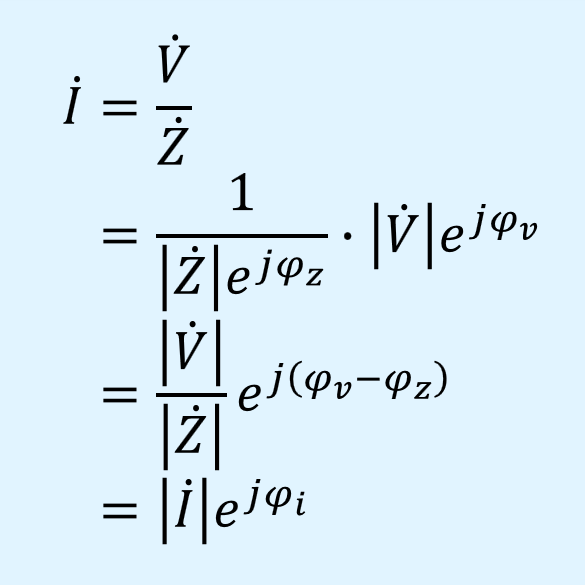

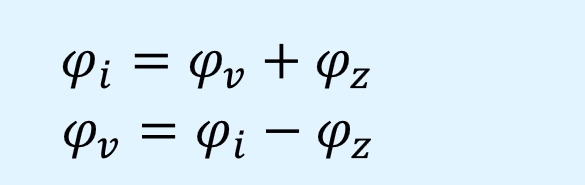



コメント