枝電流法

【まとめ】枝電流法

枝電流法による回路解析方法

枝電流法(Branch Current Method)はキルヒホッフの第1、2法則を用いた基本的な回路解析方法です。
枝電流解析法とも呼びます。

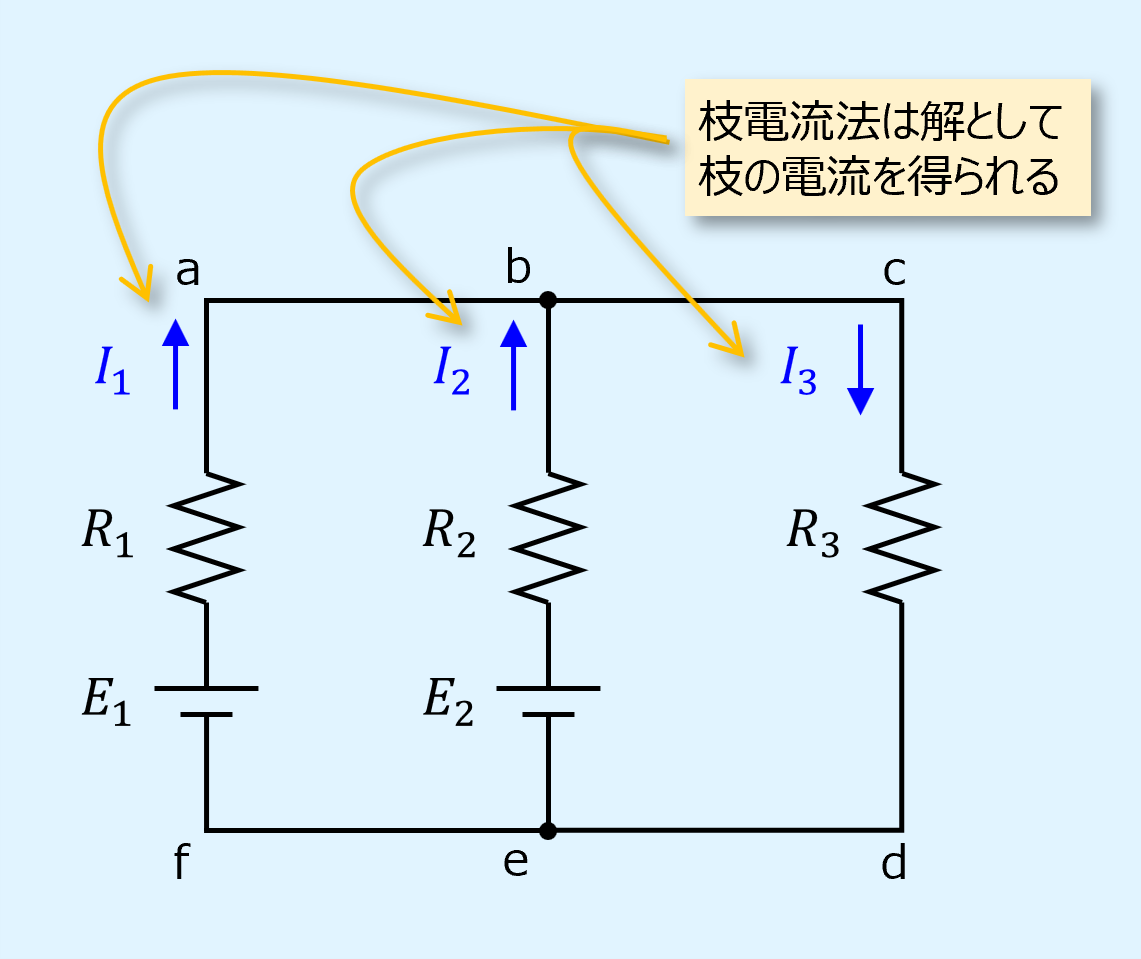
回路の要素同士が接続される点を接点と呼び、接点を結ぶ線を枝と呼びます。
解として枝の電流を得られることから枝電流法と呼びます。

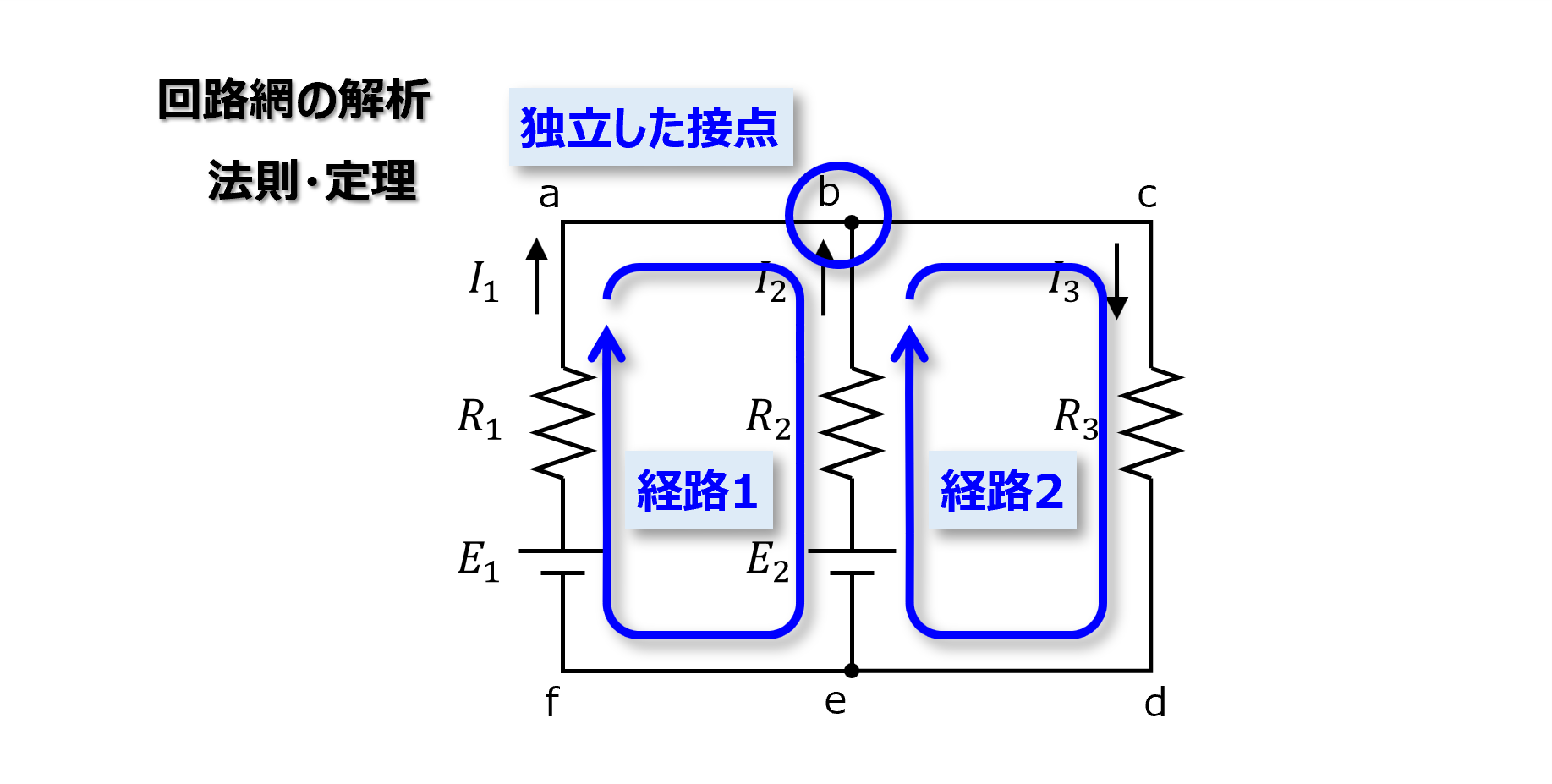
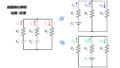
枝電流法の説明を以下の回路を用いて行います。

最初に枝電流の向きを決める必要がありますが、これはどちらでも構いません。
演習問題等で定義されているならその通りでいいし、自分で決めないといけない場合は適当に右回りにでもしておくか、電圧源の向きにでもすればよいです。
最終的に計算結果として向きがあっていれば正の値になるし、向きが違っていれば負の値として得られます。

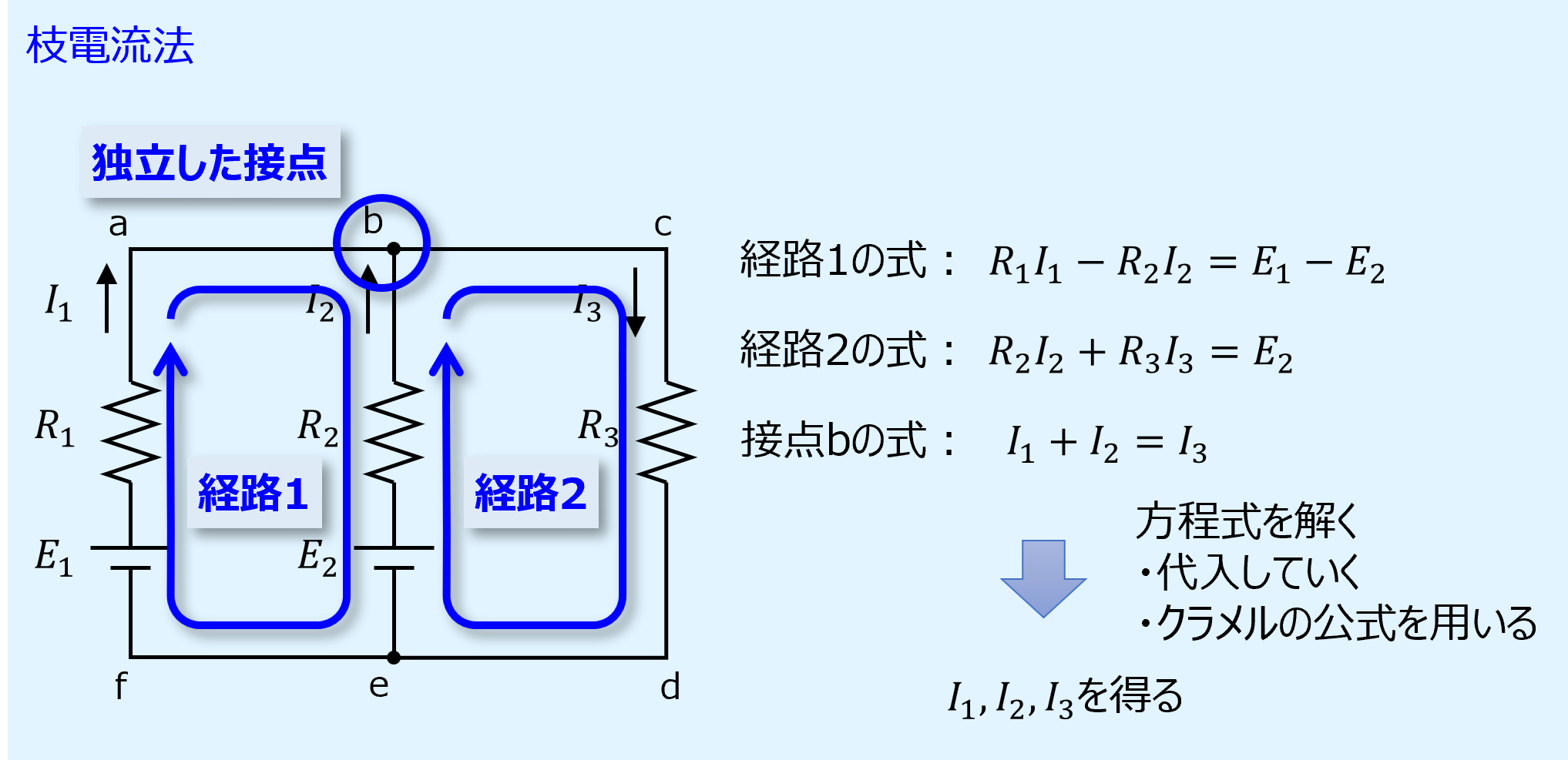
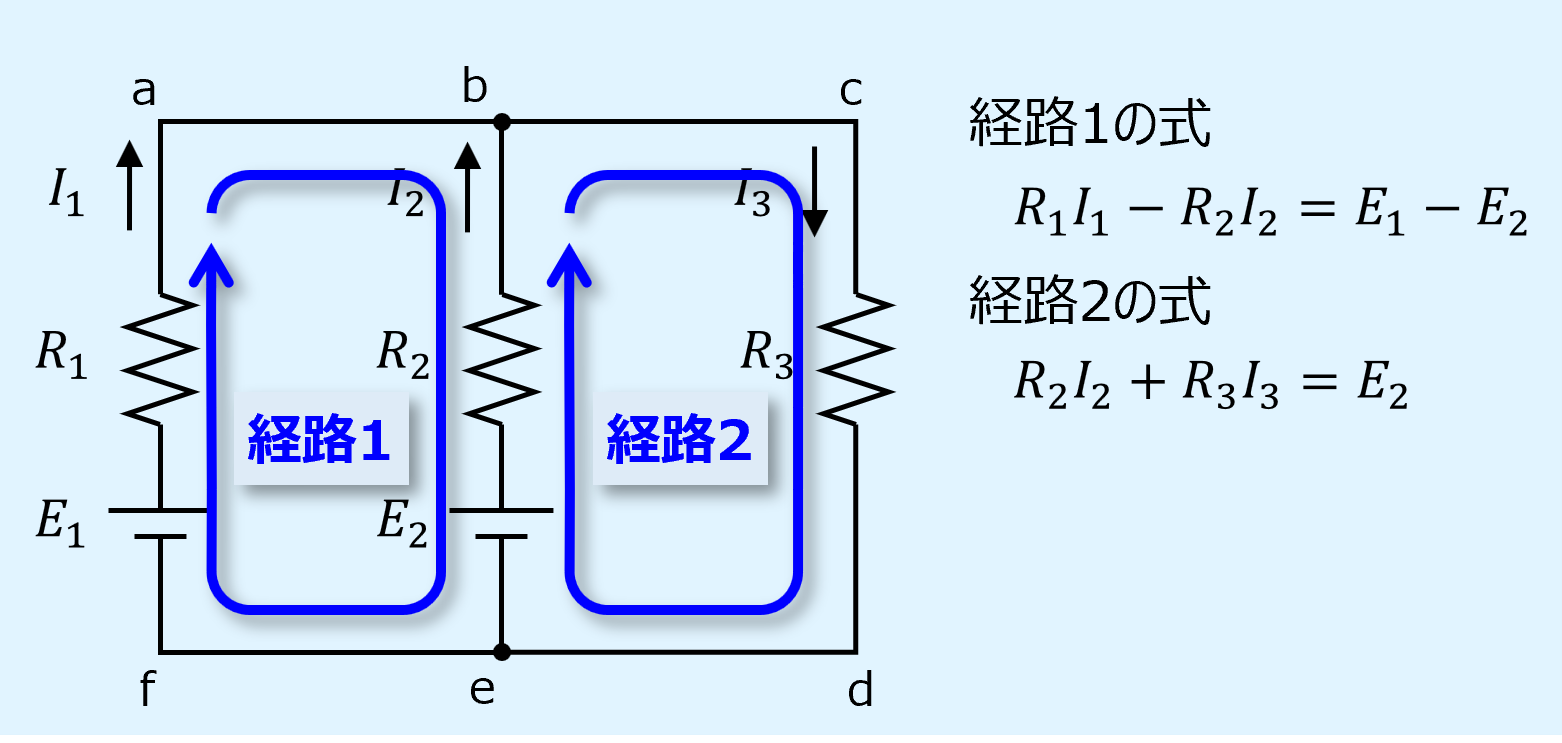
次に独立した閉回路を選択し、各閉回路でキルヒホッフの第2法則(電圧則)を適用し、式を立てます。

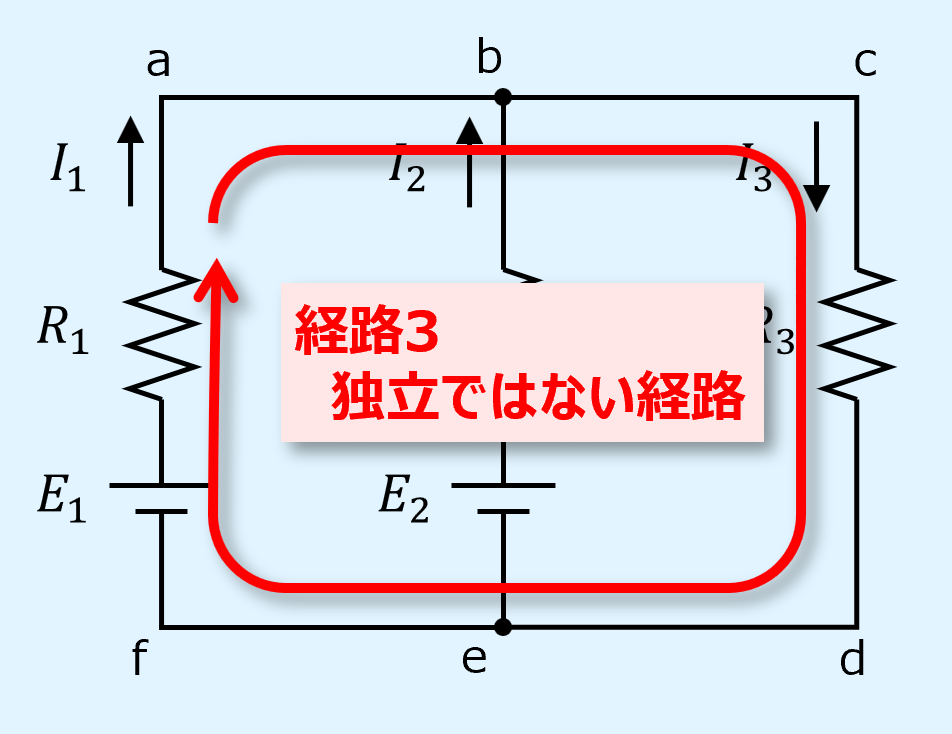
ここで、独立した閉回路とは他の閉回路を内包しない回路のことです。
例えば下図の経路は経路1と経路2を内包するので独立した経路ではありません。
独立した経路を選定できないと計算が上手くいかないので注意しましょう。

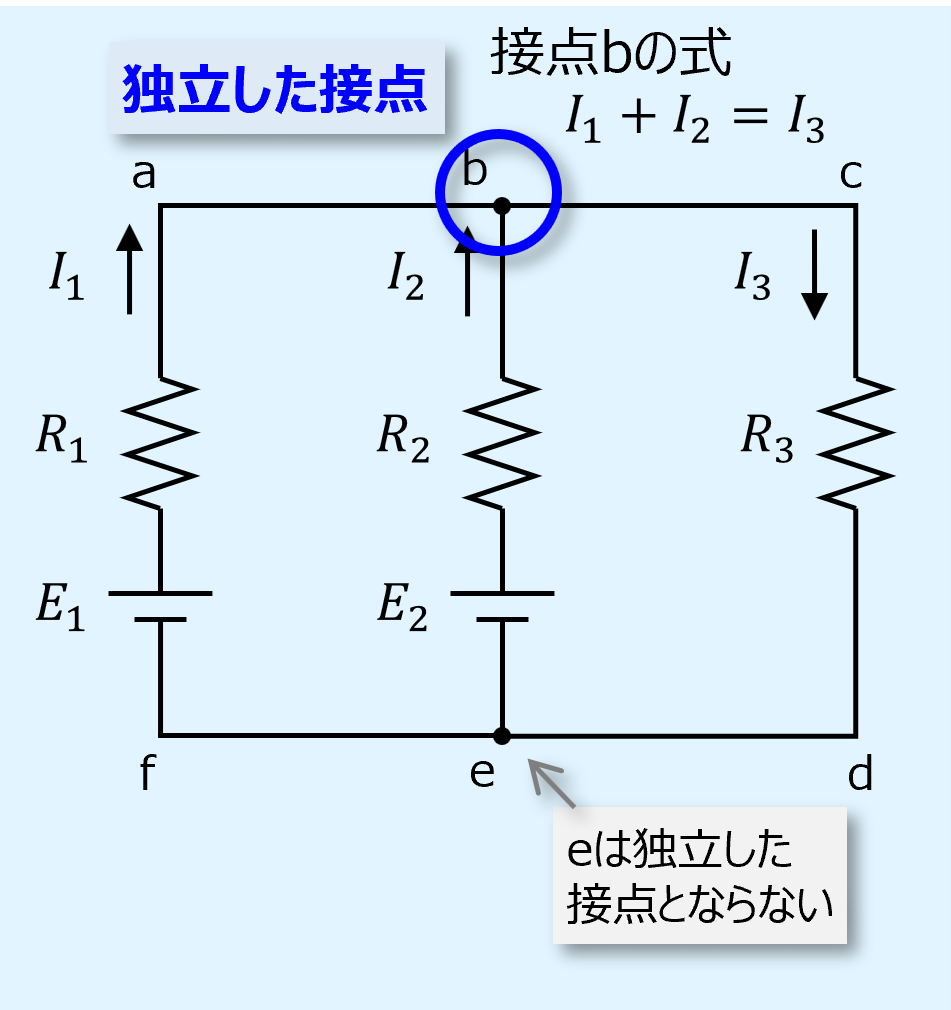
次に独立した接点を選択し、キルヒホッフの第1則(電流則)を適用して式を立てます。
ここでは接点bを選択しました。
接点bを独立した接点として選択した場合、もう一つの接点eは独立した接点とはなりません。
接点eの式は接点bの入出力を入れ替えただけのものになるためです。

最後に得られた式を解いて電流を得ます。
方程式の解き方は一つ一つ代入して解いてもいいですし、クラメルの公式を用いる方法もあります。

他のケースの独立した閉回路

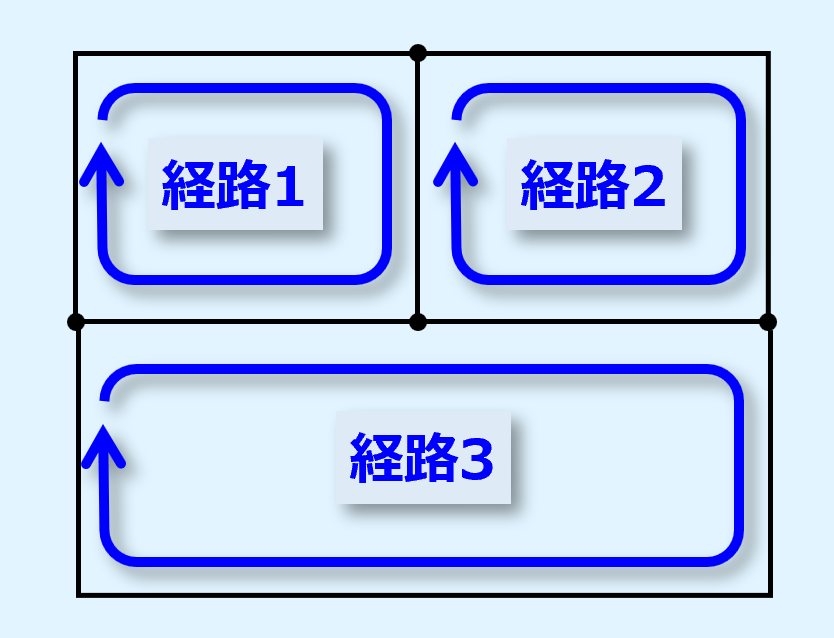
参考に他のケースにおける独立した閉回路を示します。

下図のような回路網の場合、閉回路は3つになります。
このような回路網としてはブリッジ回路があります。

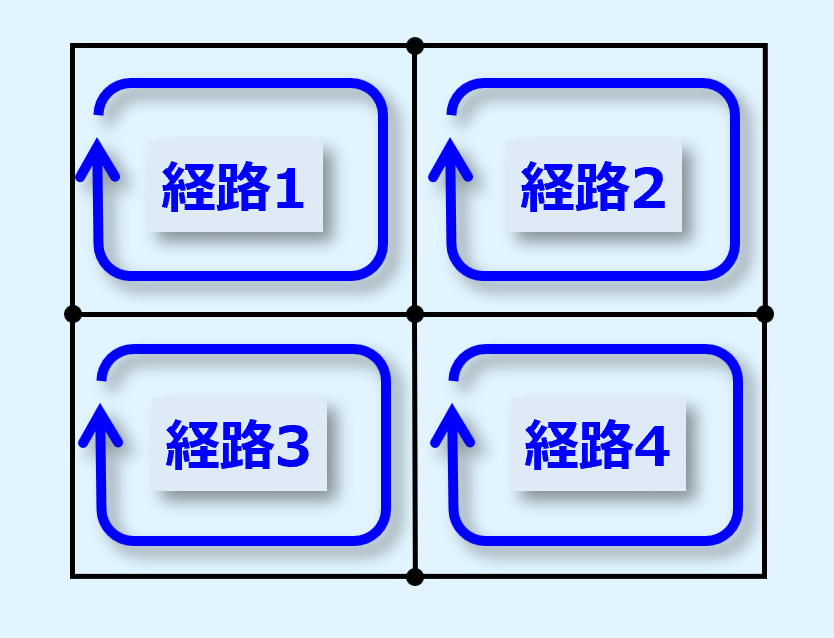
下図のような回路網の場合、閉回路は4つになります。

独立した閉回路と接点の数

独立した閉回路と接点の数は回路中の接点の数と枝の数で決まります。