この記事では電気回路で用いられるテブナンの定理について説明をします。
定理の式だけでは意味がよく分からないと思いますので、意味についても解説しています。
理解すると回路網の取り扱いが楽になりますので、双対の関係にあるノートンの定理と合わせてぜひ覚えましょう。
【まとめ】テブナンの定理
テブナンの定理とは
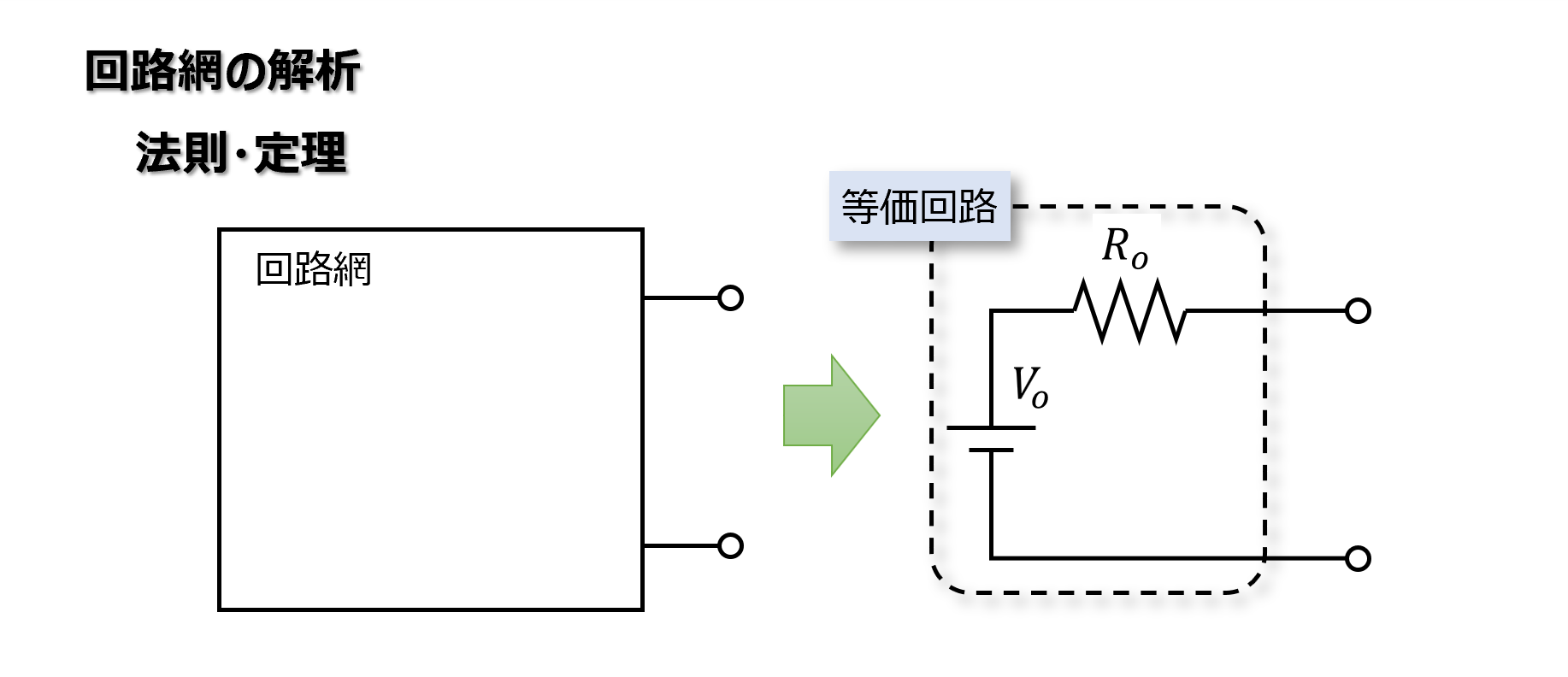
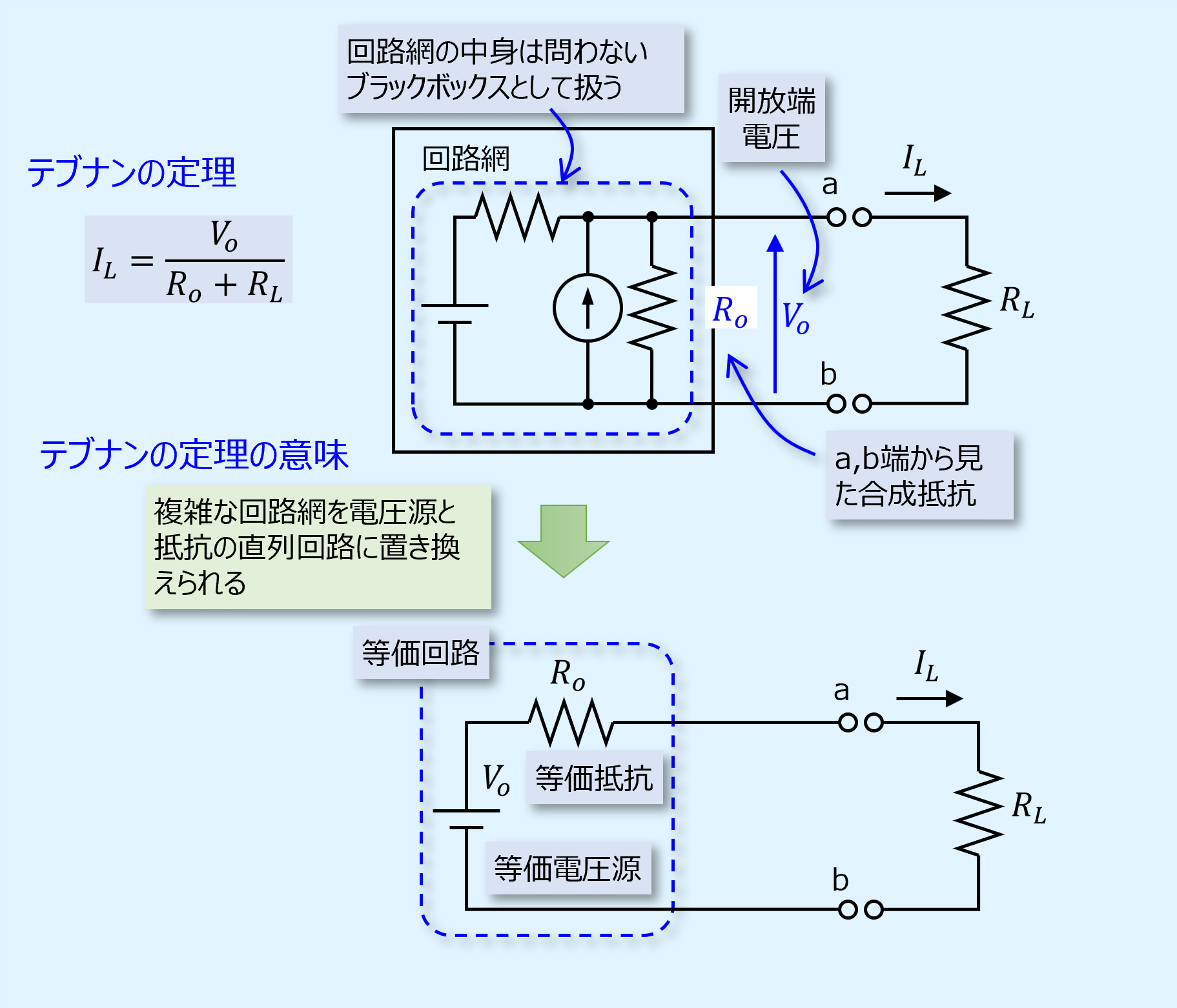
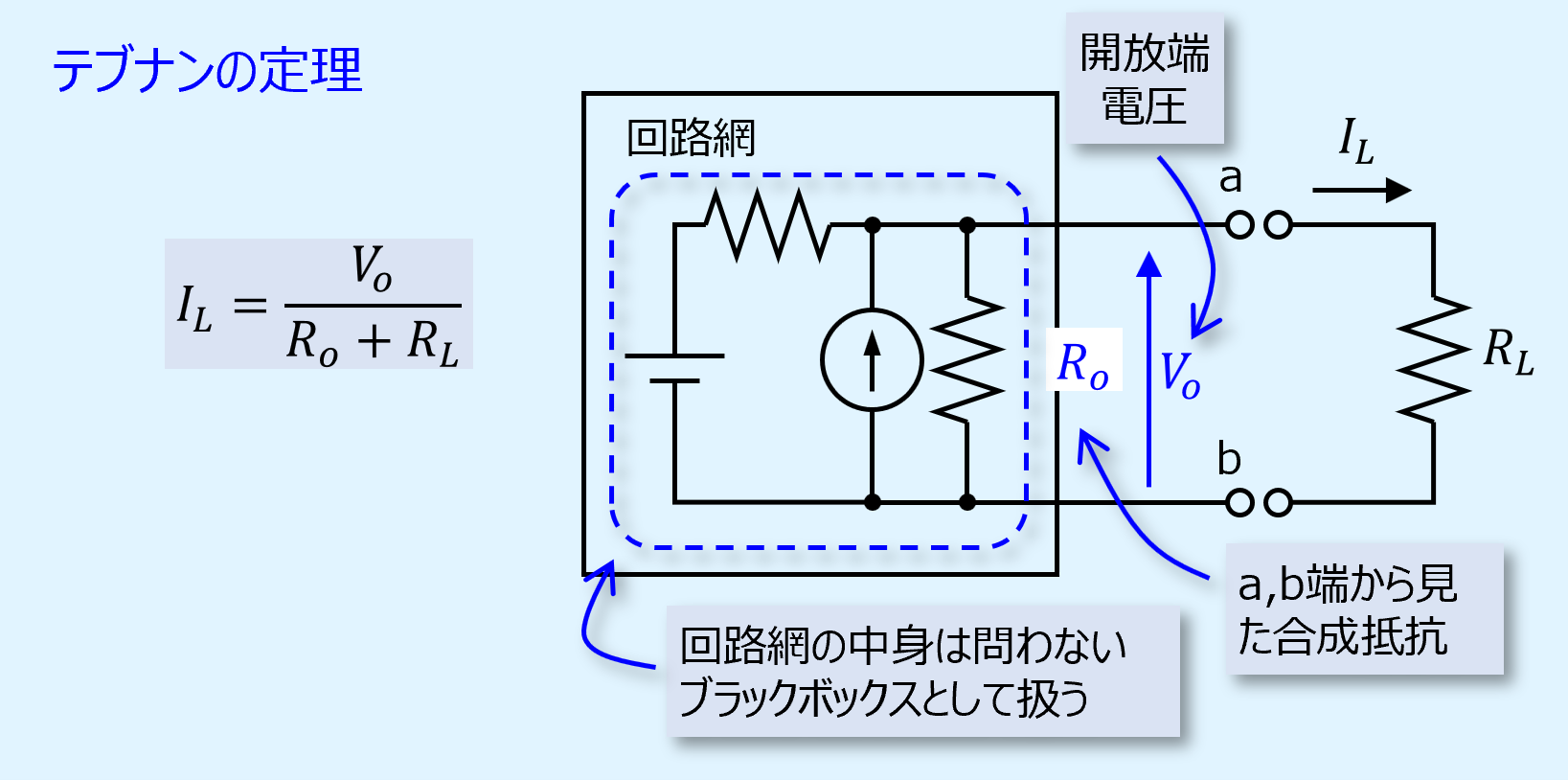
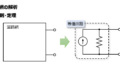
テブナンの定理(Thevenin’s theorem)は、内部に電源を含み、任意の2つの端子a,bを有する回路網へ抵抗を接続したときに、抵抗に流れる電流を表したものです。
端子a,bを開放端にした場合の電位差を\(𝑉_𝑜\) 、合成抵抗を\(𝑅_𝑜\)とし、端子a,b間に抵抗\(𝑅_𝐿 \)を接続すると、\(𝑅_𝐿 \)に流れる電流\(I_L\)は、下図のように表すことができ、この式関係をテブナンの定理といいます。
ここで回路網の中身は問わず、ブラックボックスとします。
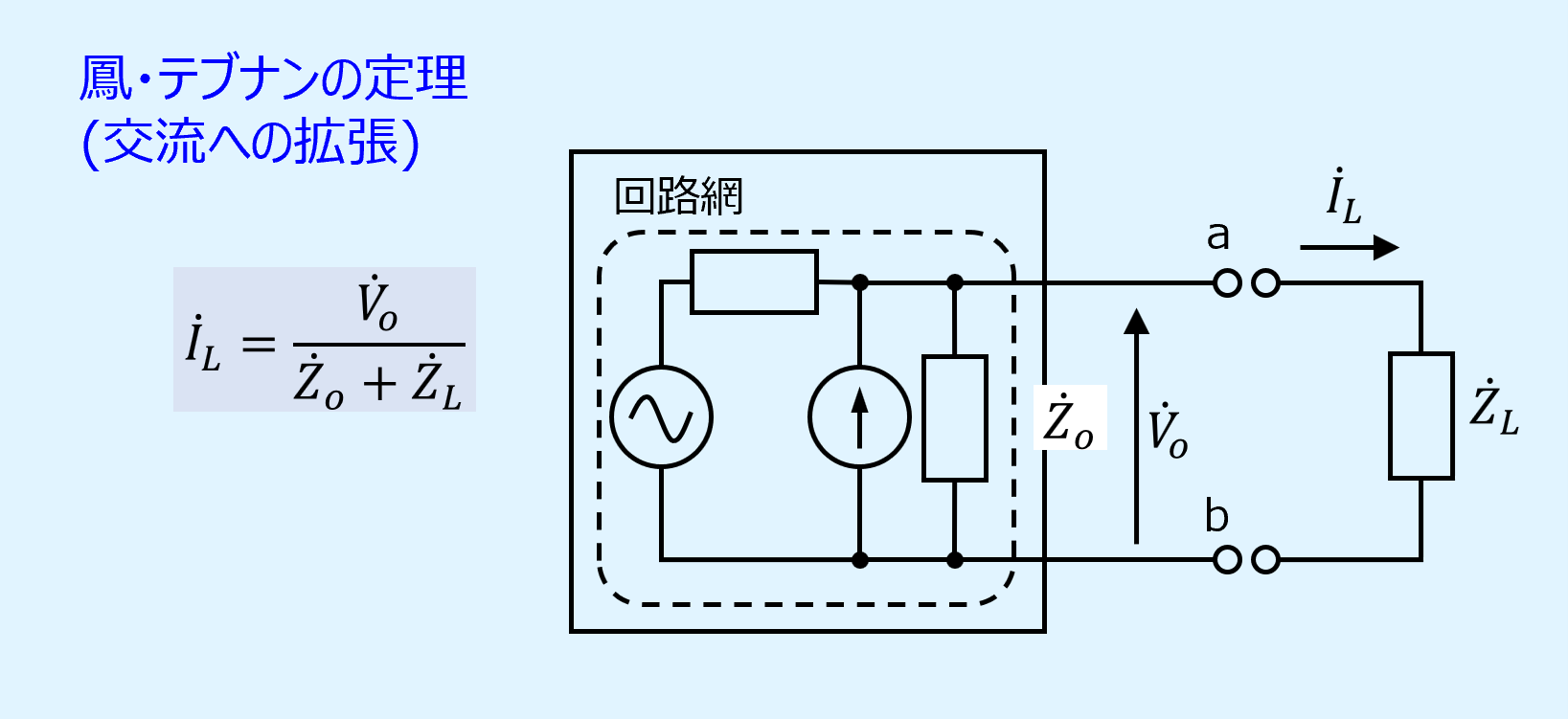
テブナンの定理は直流だけでなく交流においても成り立ちます。
そのことを発表した鳳氏の名前にちなんで鳳・テブナンの定理とも呼ばれます。
先ほどの図の抵抗をインピーダンスに置き換えると以下になります。
また、合成抵抗算出の際に電圧源は短絡、電流源は開放端として処理を行います。
なぜそうするのかは証明の個所で説明をします。
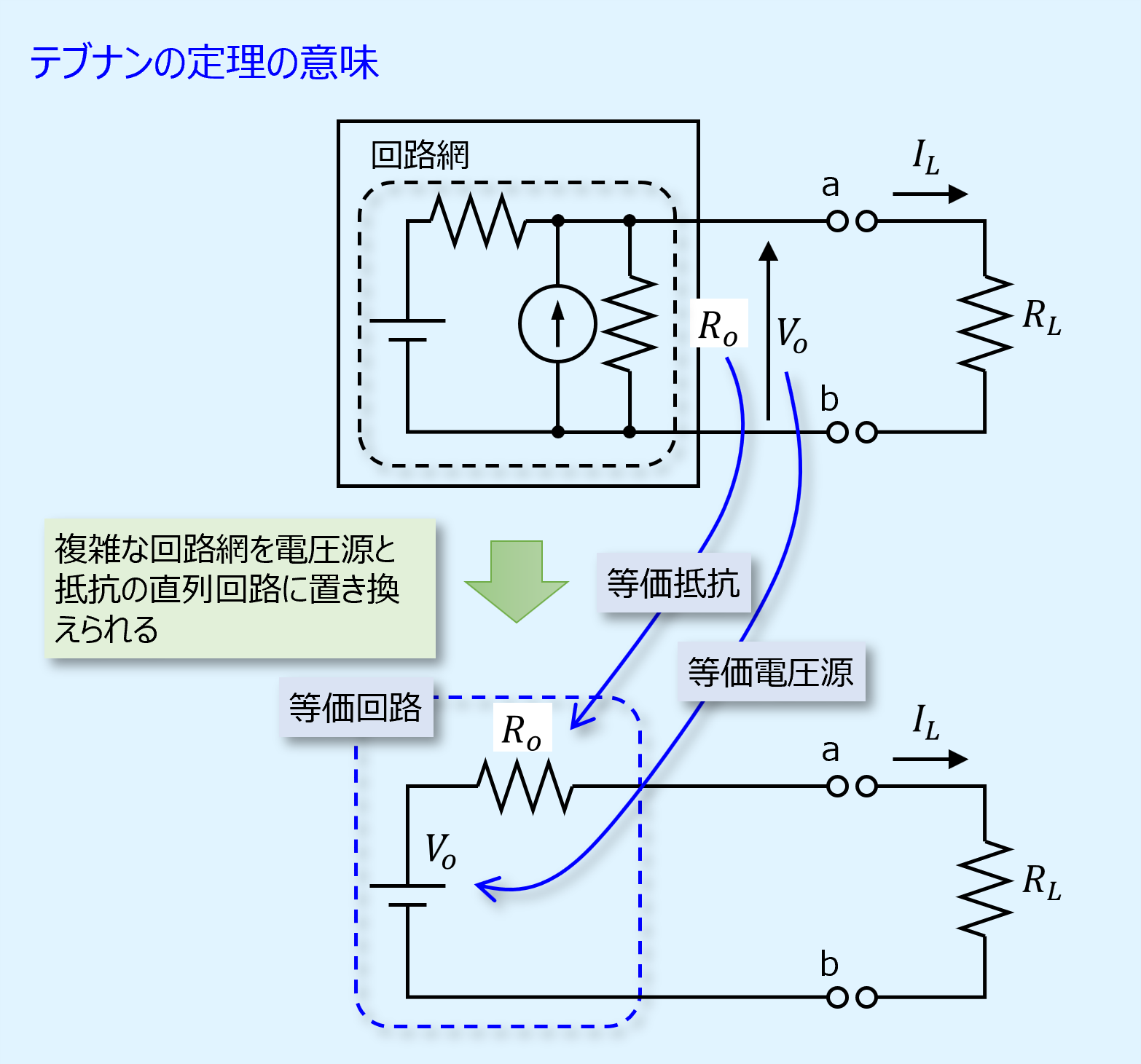
テブナンの定理の意味
定理の数式から以下のことが言えます。
回路網の任意の2端子に関する等価回路は、2端子間の電位差に等しい起電力を持つ電圧源とその間の合成抵抗との直列回路で表すことができる。
つまり複雑な回路網をその出力特性から単純な等価回路に変換でき、回路の取り扱いが容易となります。
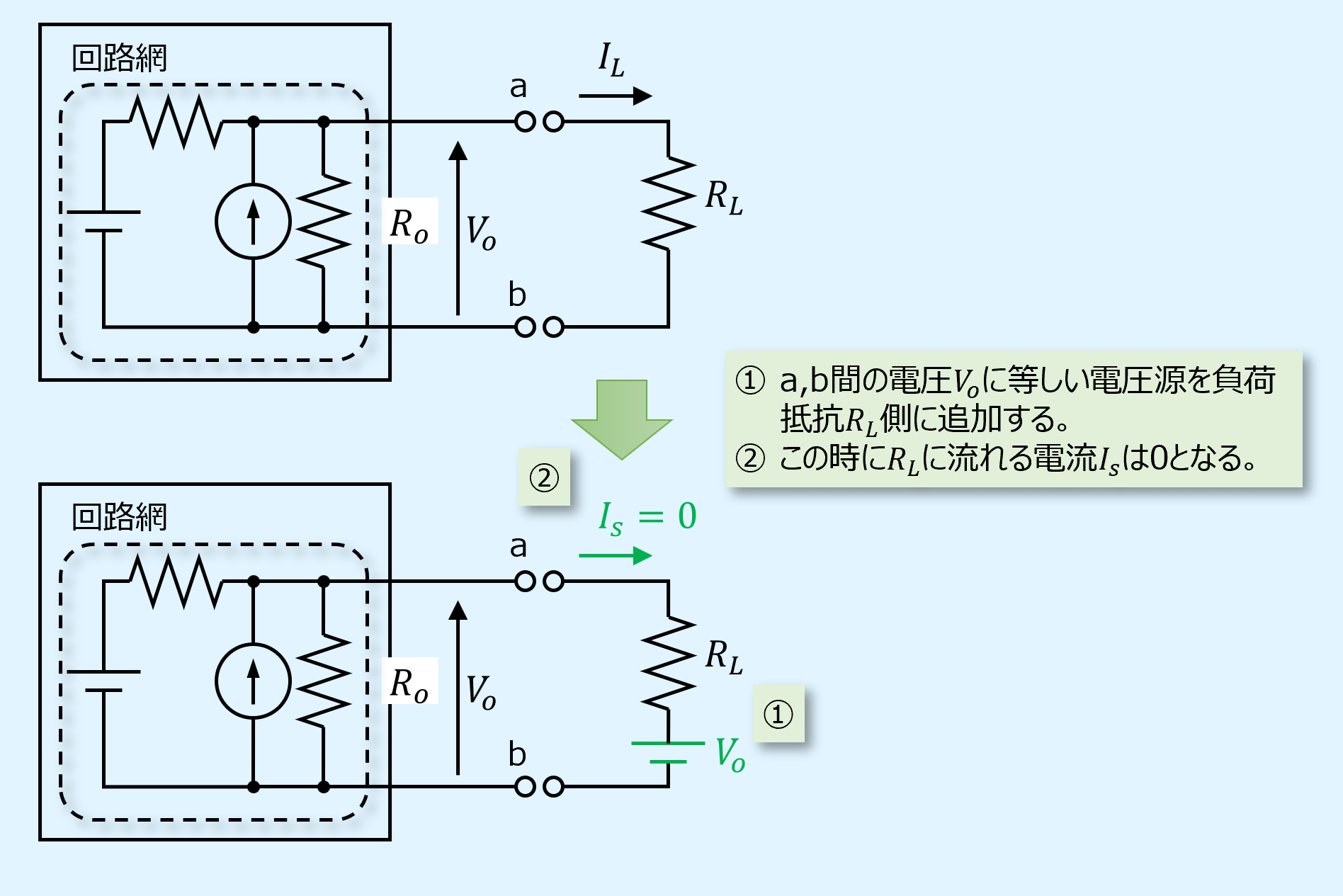
テブナンの定理の証明
証明を行うために、まず負荷抵抗\(R_L\)の方へ直列に電圧源を入れます。
この電圧源はa,b間の開放端電圧\(V_o\)に等しくします。
この時負荷抵抗\(R_L\)に流れる電流\(I_s\)は、a,b間電圧と電圧源の大きさが等しいため\(I_s=0\)となります。
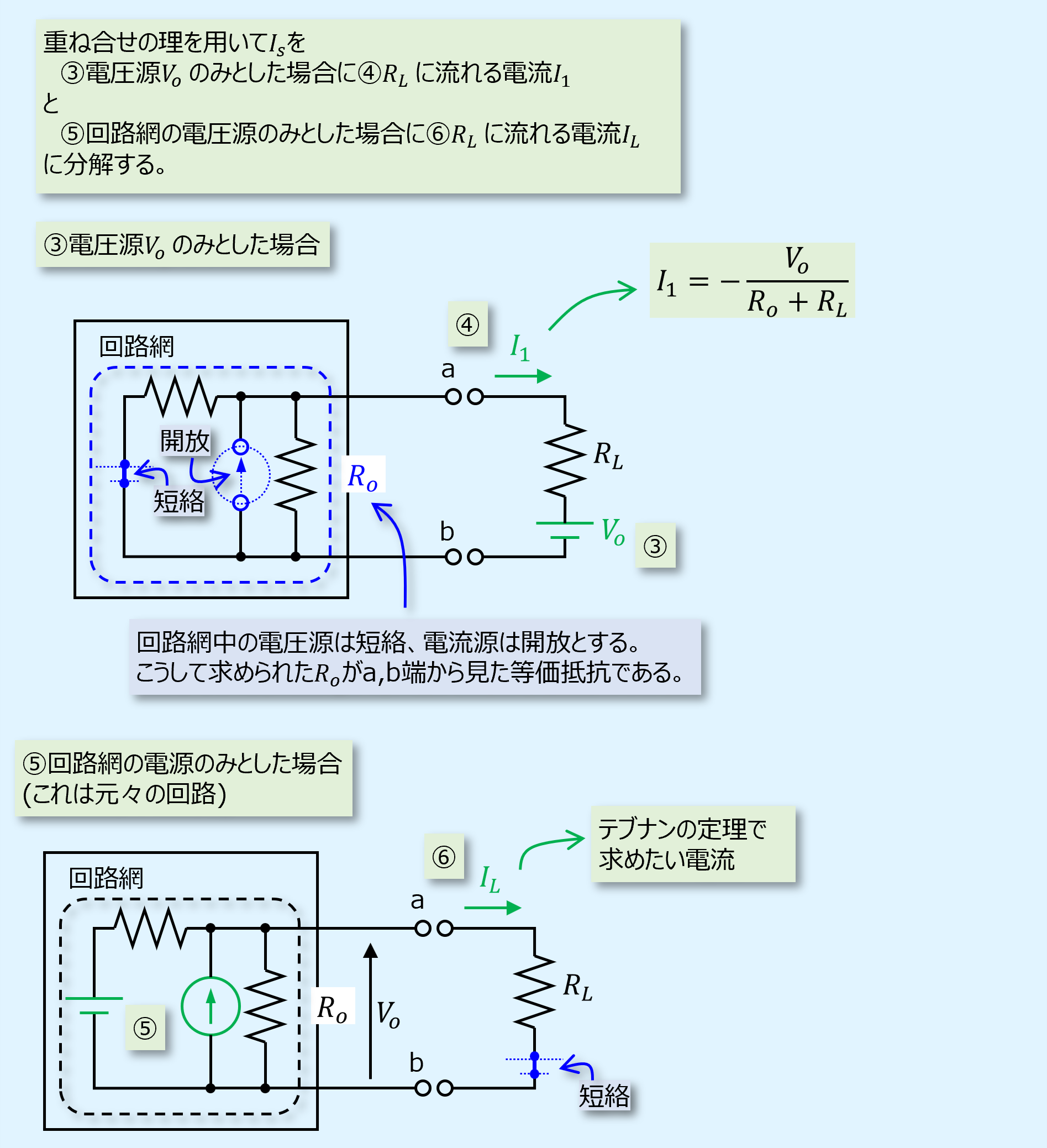
次に重ね合せの理を用いて\(I_s\)の値を求めることにします。
右端の電圧源\(V_o\)のみとした場合と、左端の回路網の電源のみとした場合の2つに分解します。
また、重ね合せの理を用いるため、無視する電圧源は短絡、電流源は開放端として扱います。
最後に重ね合せの理の結果から\(I_L\)の形に直すとテブナンの定理となります。
ノートンの定理
テブナンの定理と双対の関係にある定理として、ノートンの定理があります。
こちらについては別の記事で説明をします。

コメント