この記事では電気回路で用いられるベクトル図について説明をします。
ベクトル図とは何かから、位相の進み、遅れとの関係までを取り扱います。
目次
【まとめ】ベクトル図
最初にまとめです。
ベクトル図とは
フェーザは、実軸と虚軸からなる複素平面上で、大きさと向きを持つベクトルです。
フェーザを複素平面上に矢印としてしたものをベクトル図といいます。
以下にベクトル図の例を示します。
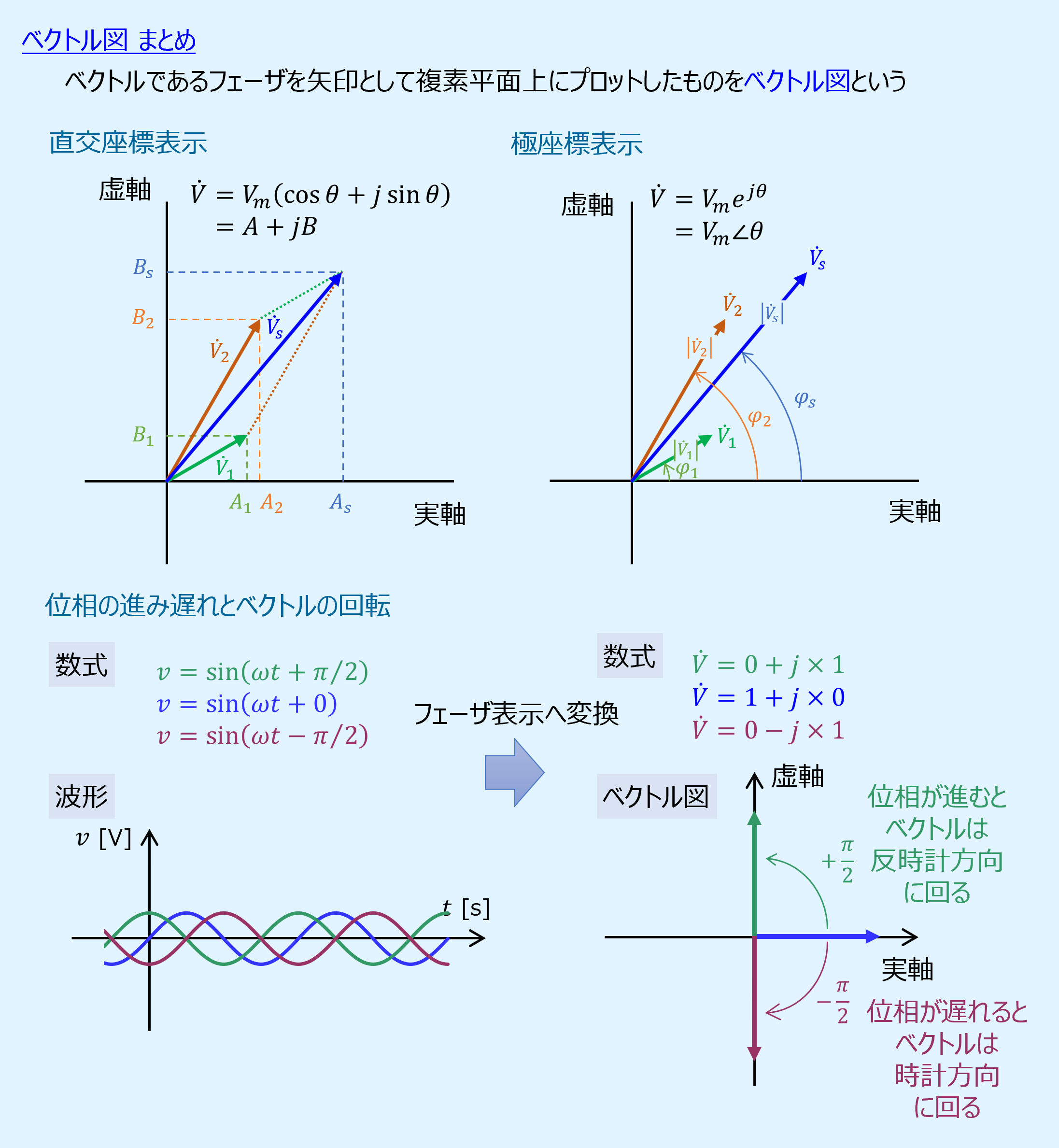
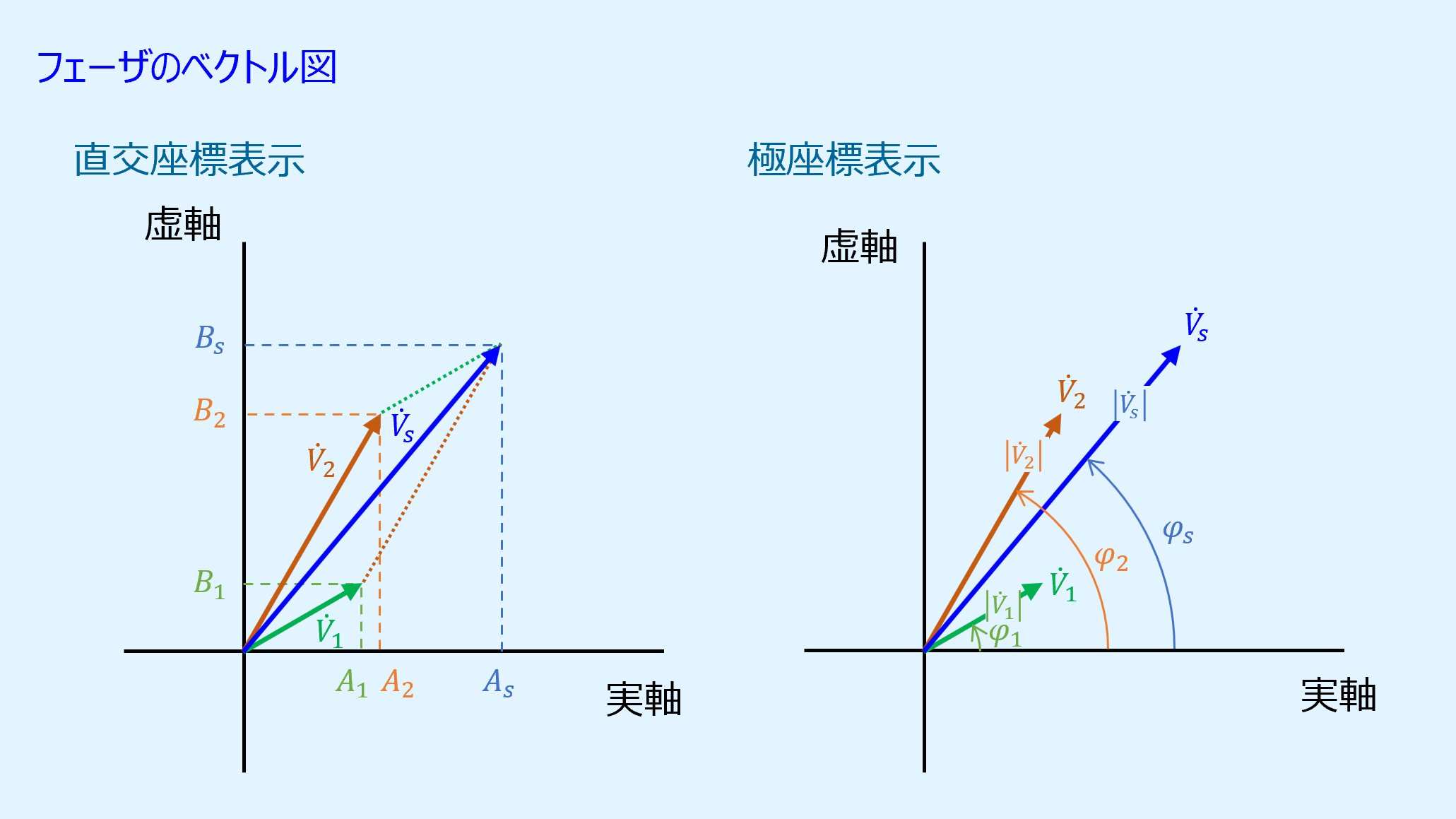
ベクトル図は直交座標表示でも極座標表示でも作成が可能です。
ここで、フェーザ\(\dot{V}_1\)、\(\dot{V}_2\)を加算すると\(\dot{V}_s\)となります。
直交座標表示では、原点から実数部、虚数部の値まで矢印を引きます。
極標表示では、ベクトルの大きさと矢印の長さを同じとし、位相と同じだけ矢印を傾けます。
直交座標表示でも極座標表示でもベクトルを表す矢印は同じになる点に注意しましょう。
このように平面上にプロットすることで視覚的にフェーザの計算を理解することが可能となります。
位相の進み、遅れとベクトル図の関係
先の説明で、極座標表示では位相と同じだけベクトルを表す矢印が傾くと述べましたが、具体的に位相がどうなるとベクトルがどう傾くのか理解しておきましょう。
以降で、位相に進みと遅れがない場合(基準)、位相が90°進んでいる場合、位相が90°遅れている場合、位相が45°進んでいる場合を示します。
なお、位相と傾きの関係のみを理解するため、フェーザの大きさは全て1としています。
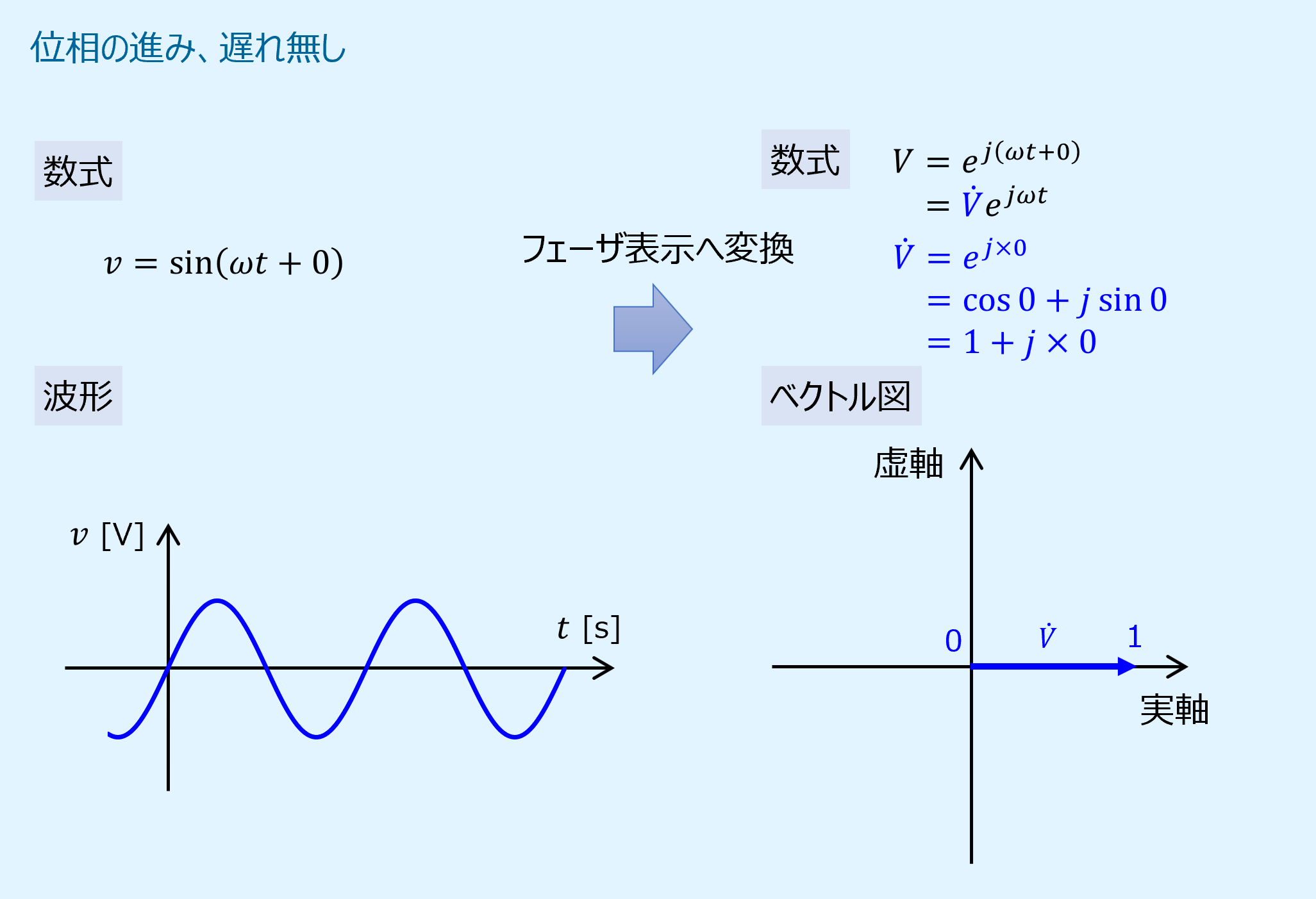
位相に進みと遅れが無い場合のベクトル図
最初に位相の進み、遅れがない場合の正弦波波形とベクトル図を示します。
位相に進み遅れがない場合、すなわち基準となる場合は、矢印は実軸方向に沿って引かれます。
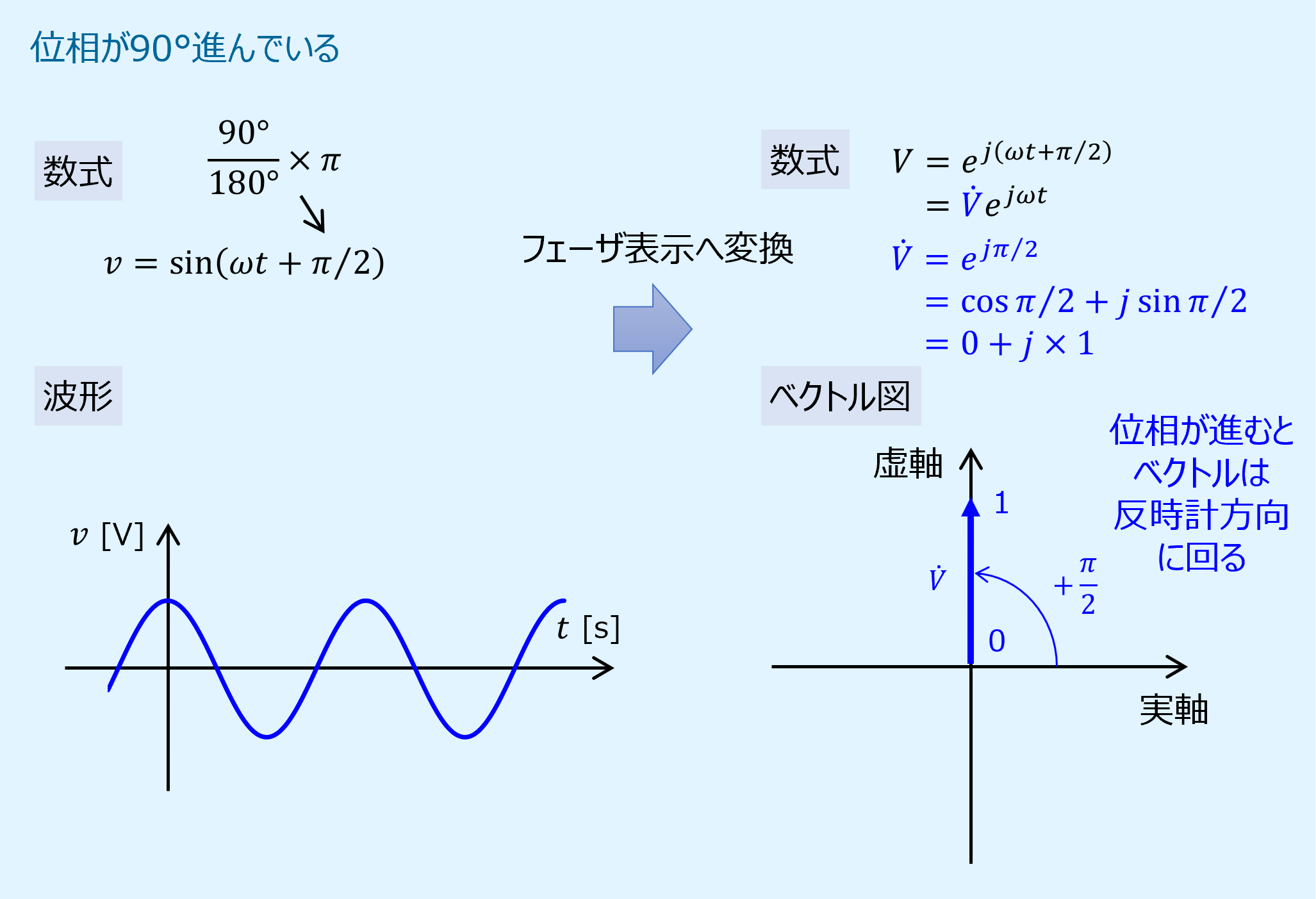
位相が90°進んでいる場合のベクトル図
次に位相が90°進んでいる場合を示します。
ベクトルは虚軸の正方向に向かって引かれます。
基準となる位相の進み遅れが無い場合との比較より、位相が進むとベクトルは反時計方向に回るということが分かります。
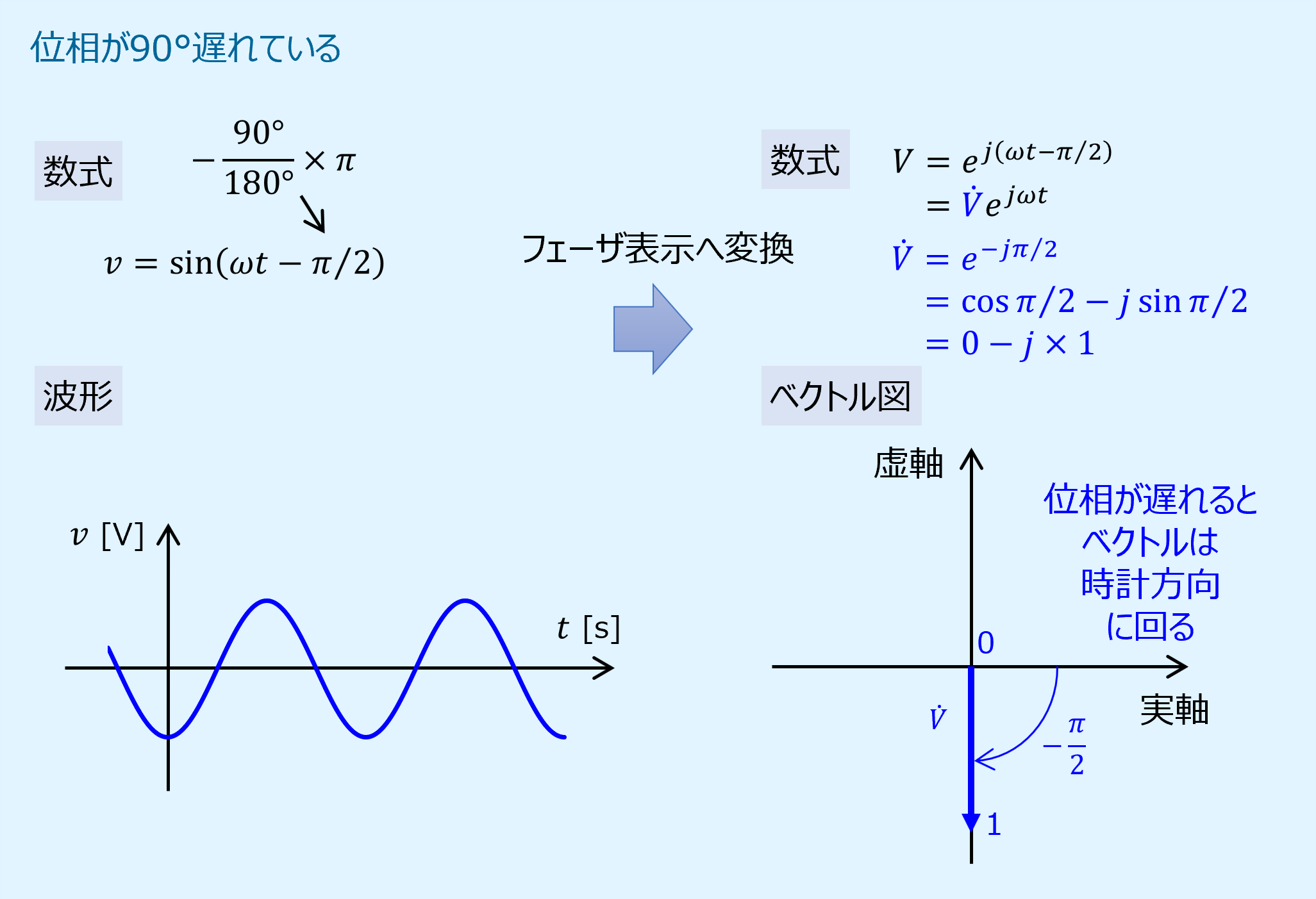
位相が90°遅れている場合のベクトル図
次に位相が90°遅れている場合を示します。
ベクトルは虚軸の負方向に向かって引かれます。
基準となる位相の進み遅れが無い場合との比較より、位相が遅れるとベクトルは時計方向に回るということが分かります。
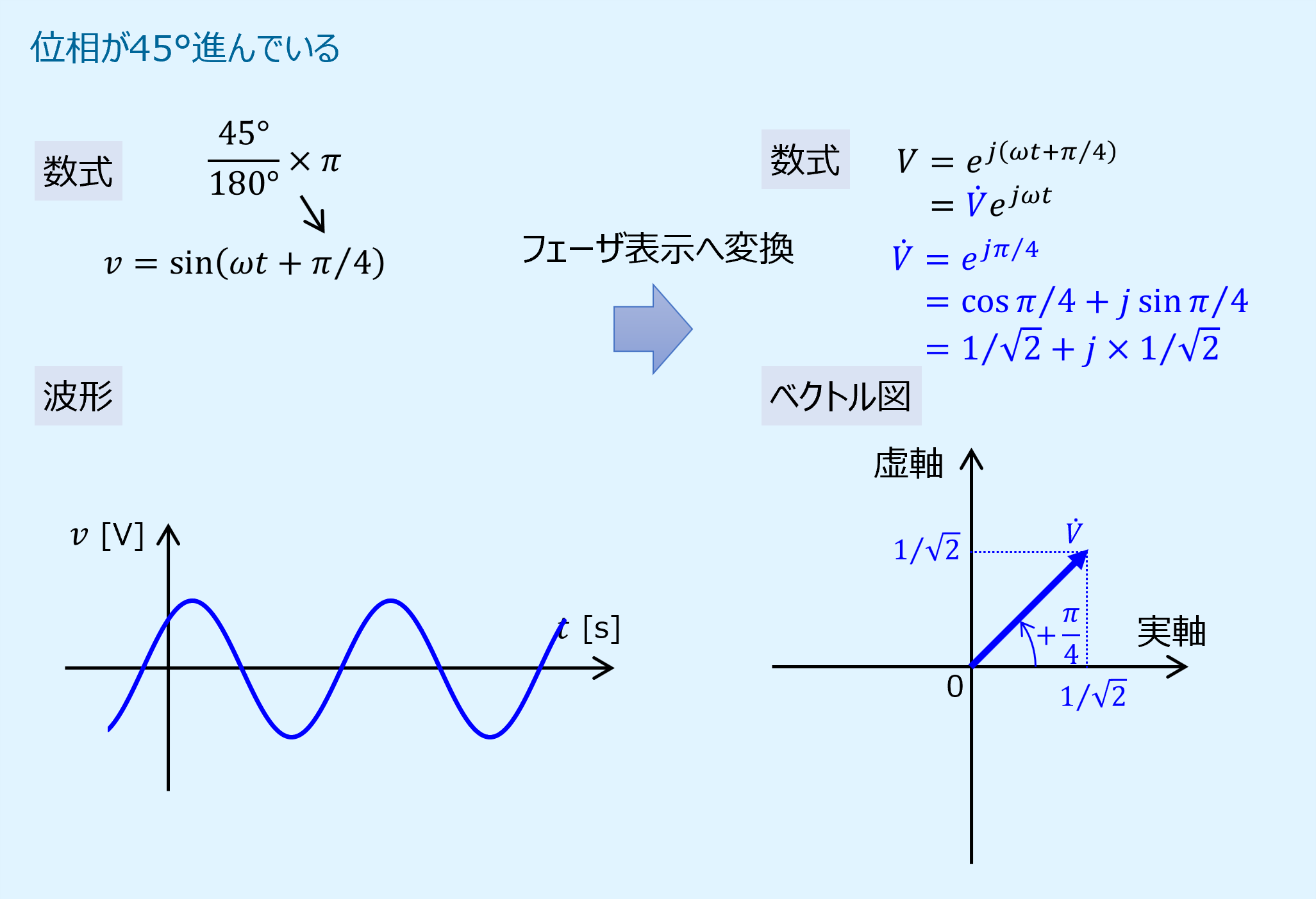
位相が45°進んでいる場合のベクトル図
次に位相が45°進んでいる場合を示します。
先に示した位相の進み遅れ無しと、90°進んだ場合の中間がどうなるかを示しています。
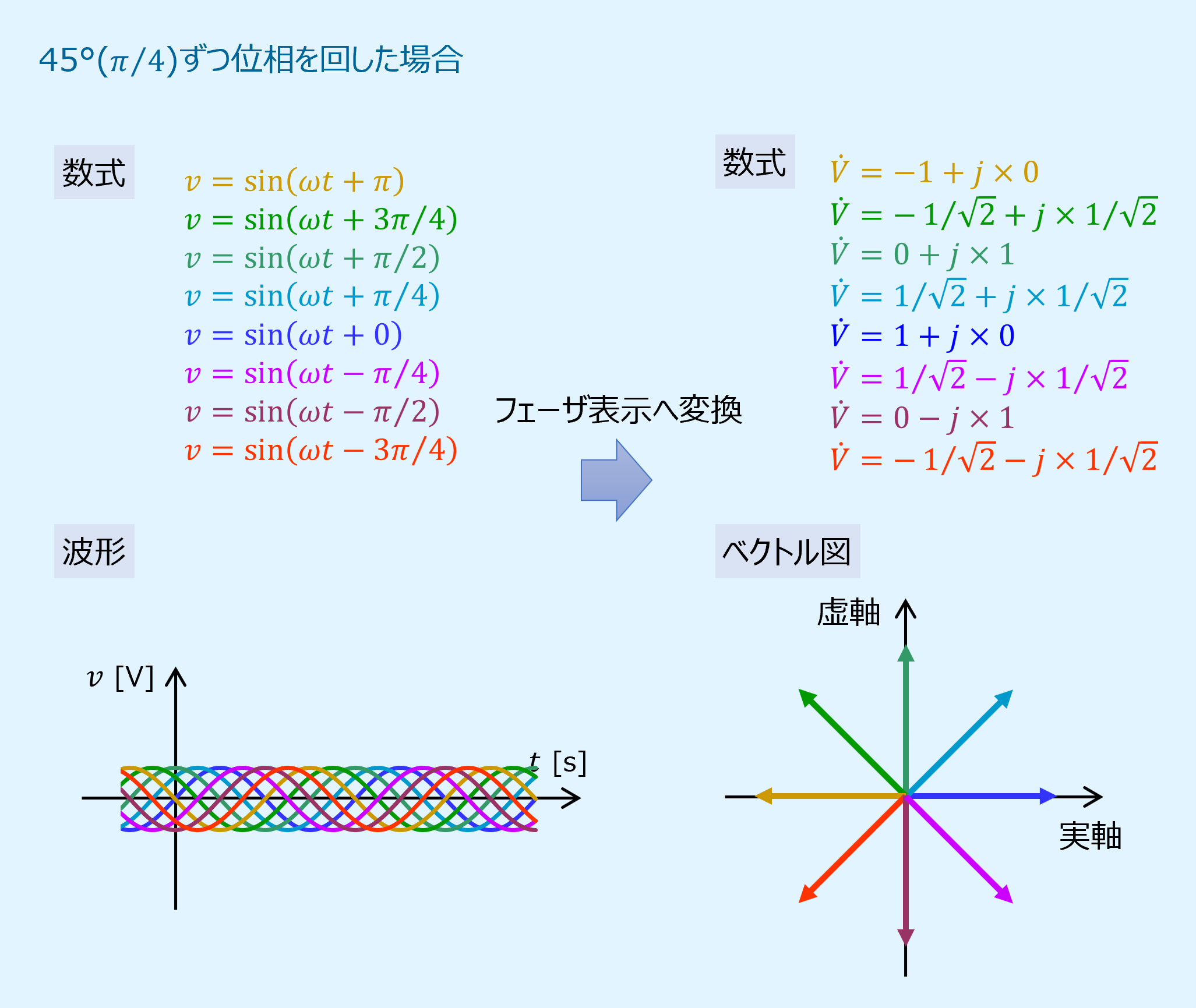
ベクトルは反時計方向に45°(\({\pi}/4\))周り、実数成分と虚数成分がそれぞれ\(1/\sqrt{2}\)になっていることが分かります。
ここでベクトルの大きさは変わらず1のままであることに注意しましょう。
位相を一周回した場合のベクトル図
最後に位相をぐるっと一周、+180°(\(\pi\))から45°(\({\pi}/4\))刻みで回した場合のベクトル図を以下に示します。
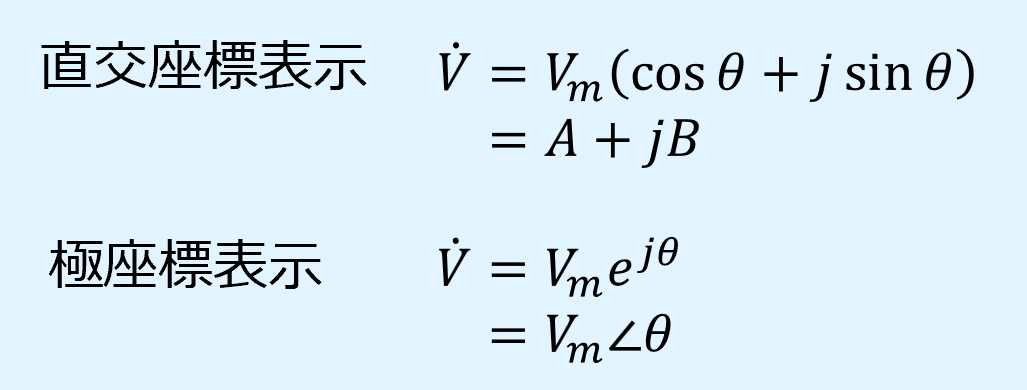
コメント