この記事では数学や情報処理で用いられる集合の演算則を取り扱います。
交換則、結合則、分配則、ド・モルガンの法則、吸収則、相補則についてベン図も交えて説明します。
はじめに
その他の法則については前回の記事をご覧下さい。
本記事では恒等則、統治則、べき等則、対合則について説明しています。
全法則のまとめもありますので参考にして下さい。
交換則
交換則(commutative laws)は、演算の順序を変えることができるというもので、以下のように表されます。
同じ集合であれば、集合記号を左右どちらに記載しても結果は変わりません。
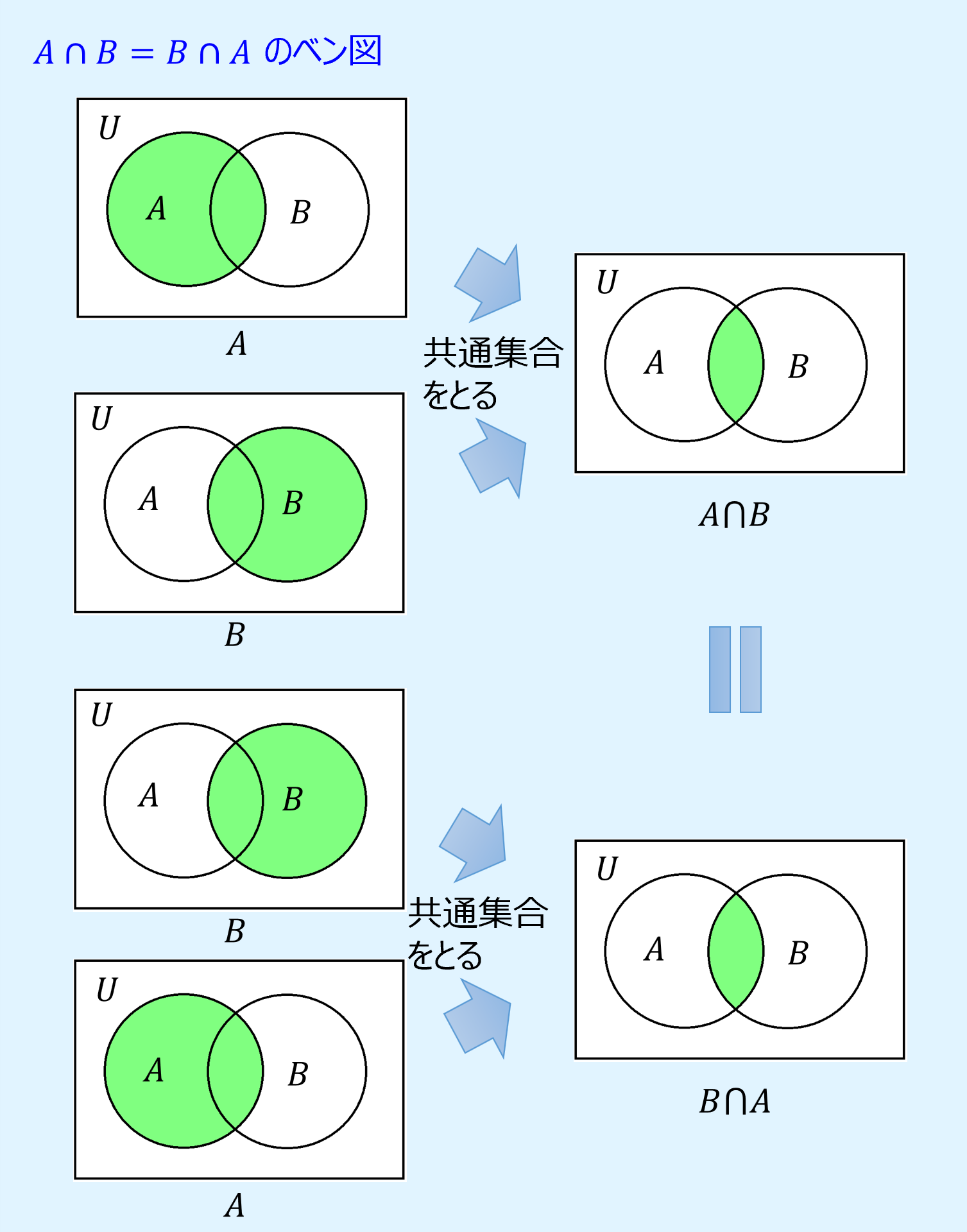
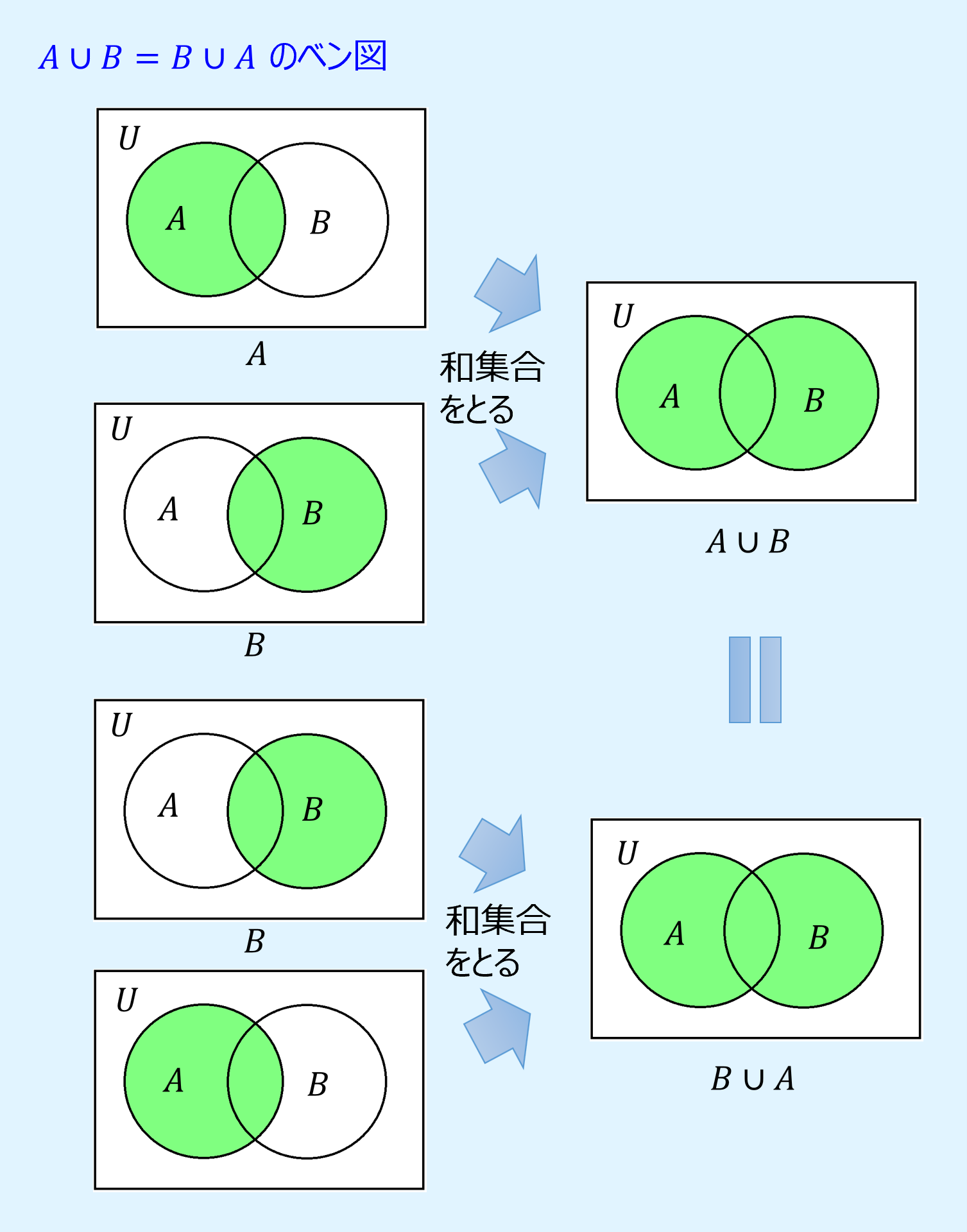
また、ベン図で交換則を表すと以下のようになります。
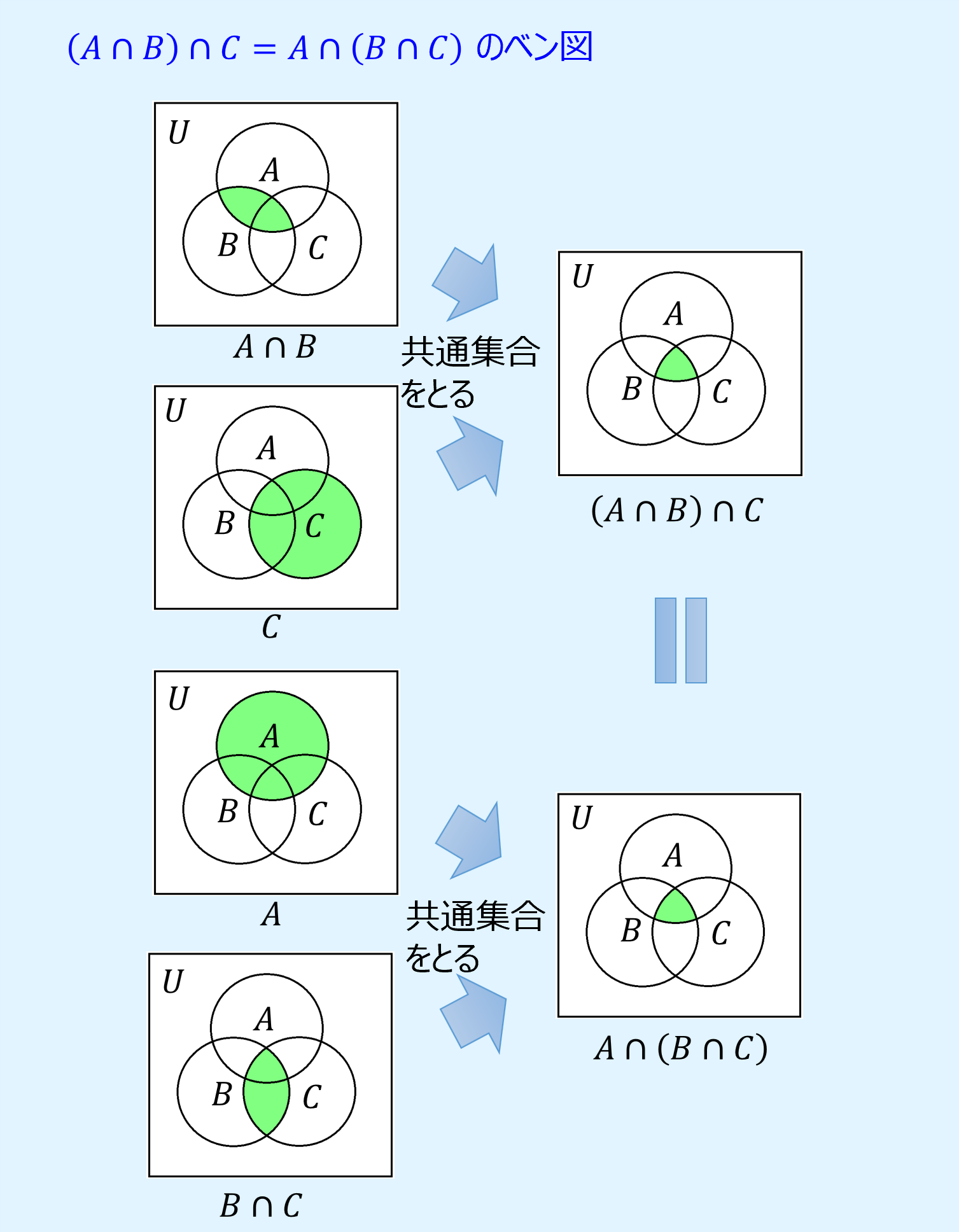
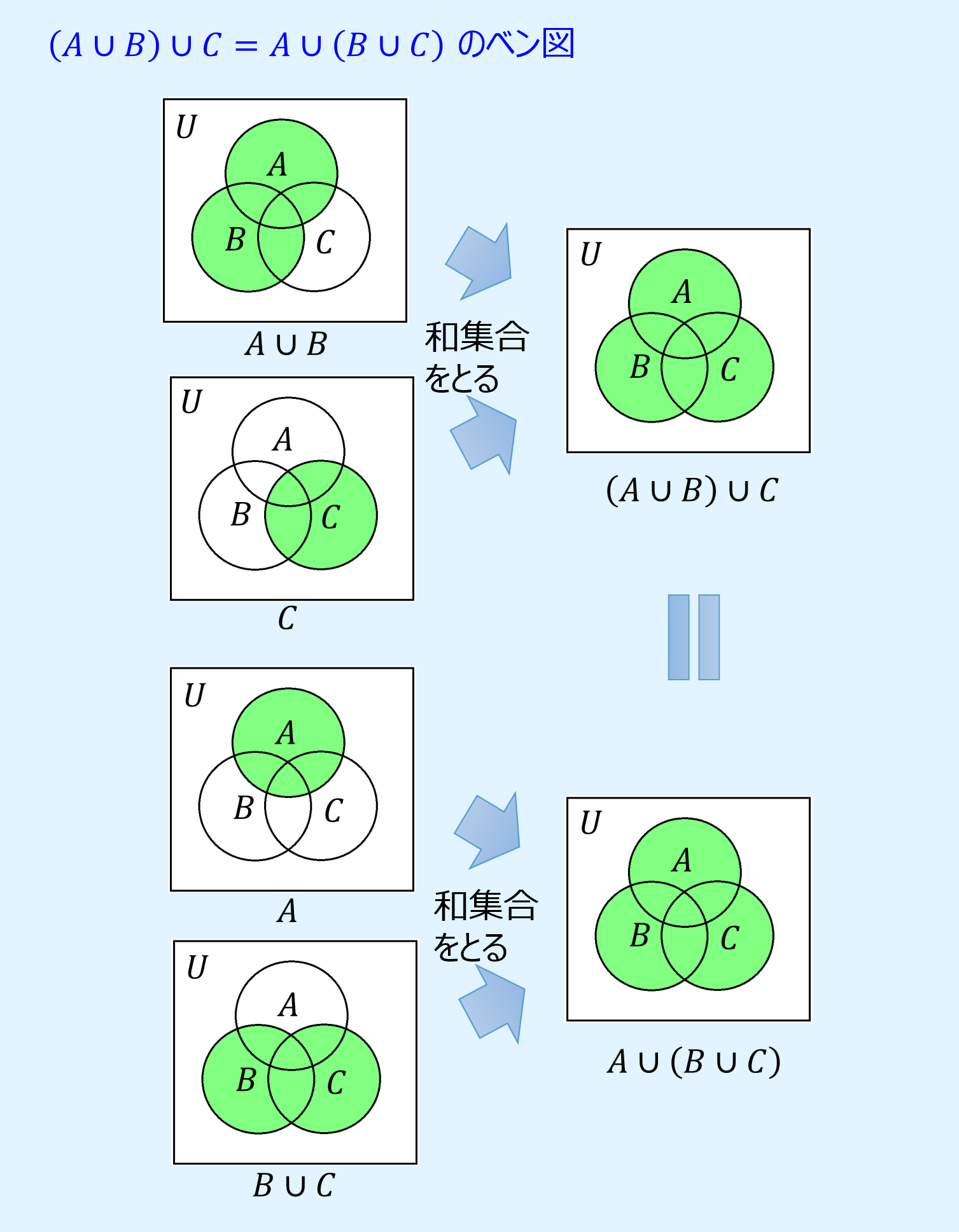
結合則
結合則(associative laws)は、同じ結合演算子が複数連続する場合、被演算子の並びを変えなければ、演算を行う順番を変えることができるというもので、以下のように表されます。
四則演算で例えると、全て同じ演算の場合は括弧の順番を入れ替えても結果が等しいことと同じです。
また、ベン図で結合則を表すと以下のようになります。
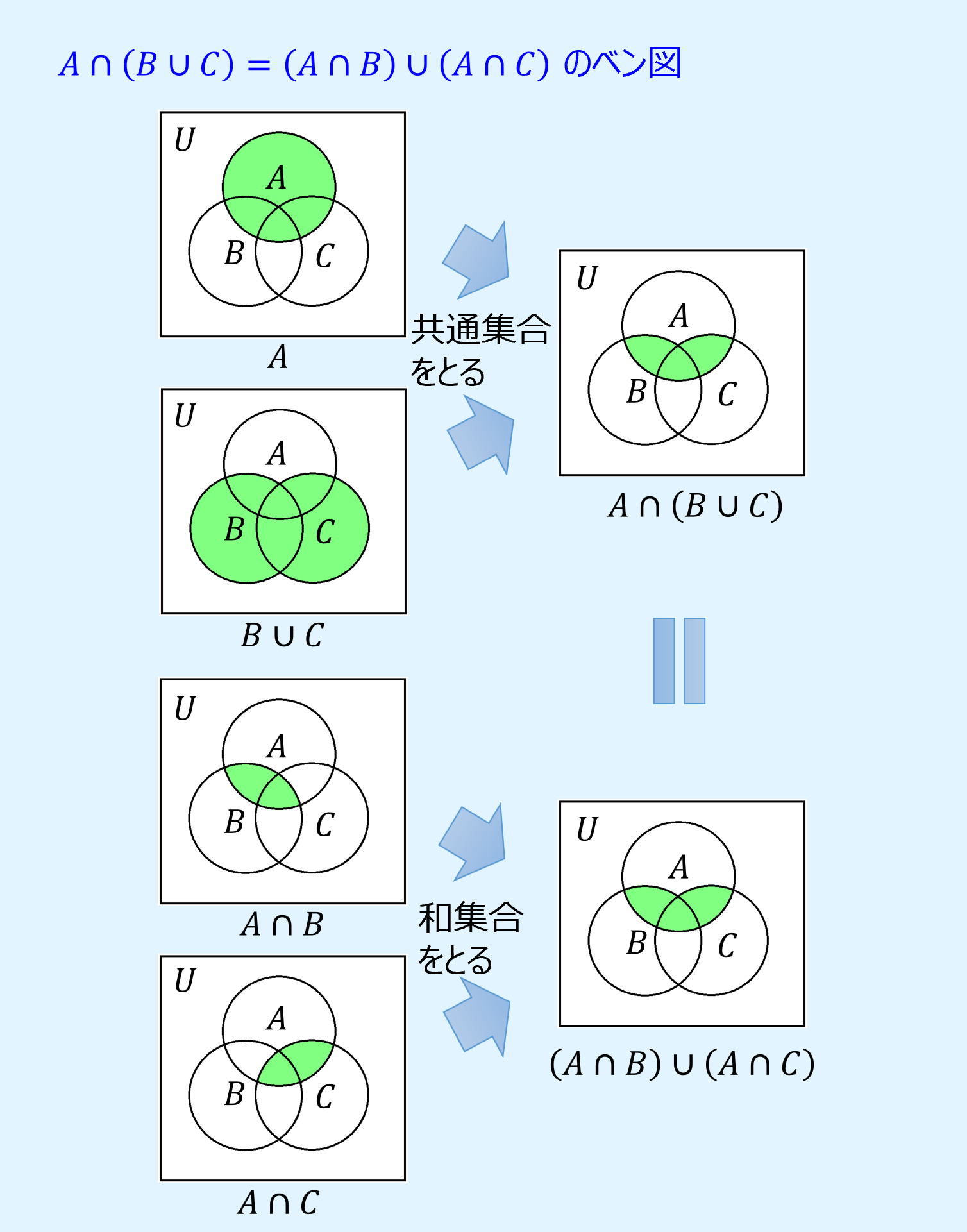
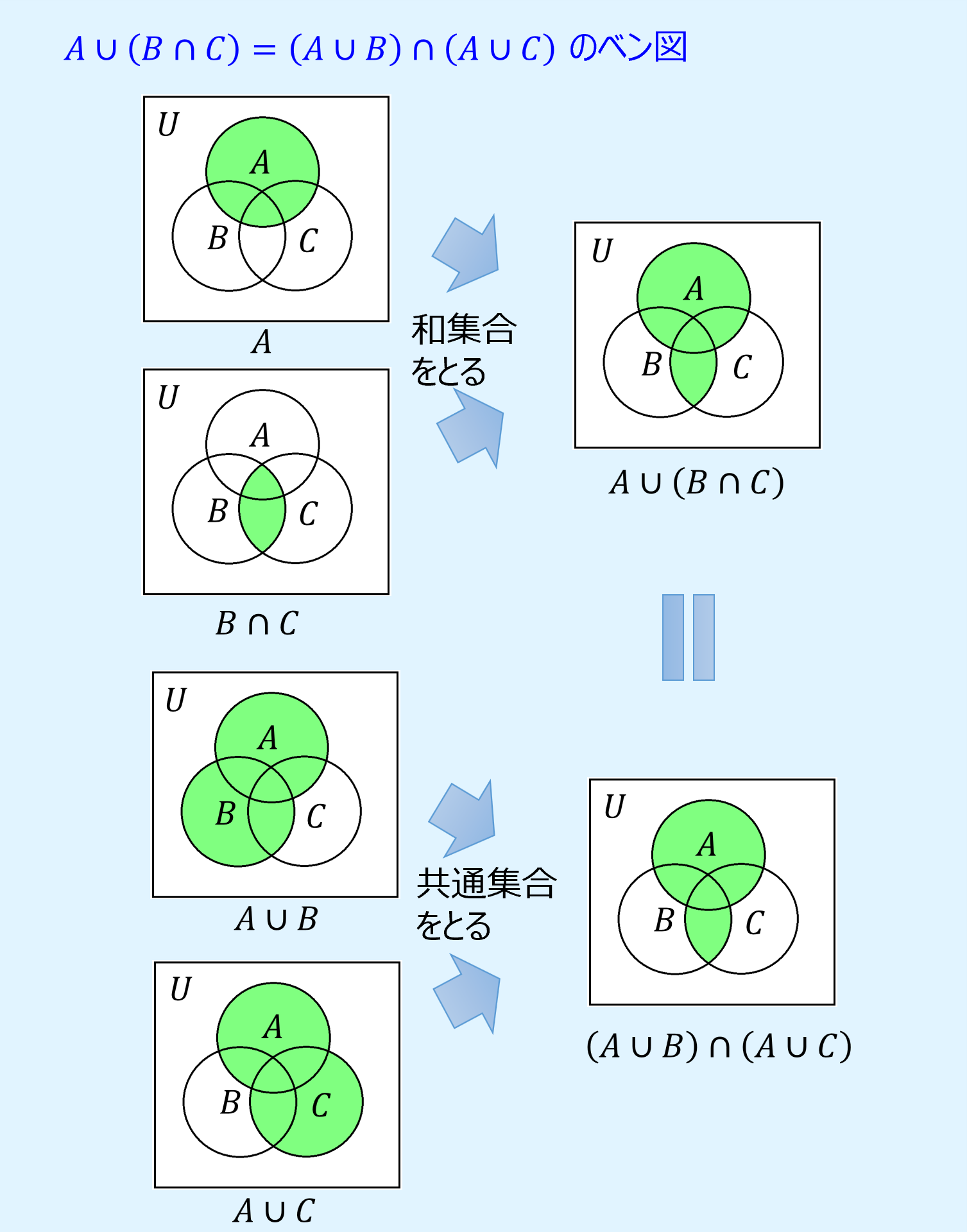
分配則
分配則(distributive laws)は、先に演算を行ったものに対し後から別の演算を行う場合、後から行う演算を最初の演算対象へ個別に行い、その結果に対して最初の演算を行っても結果は変わらないというもので、以下のように表されます。
四則演算で例えると、加減算の結果に対して乗除算を行った結果と、先に乗除算を行ったものに加減算をした結果が等しくなることと同じです。
また、ベン図で分配則を表すと以下のようになります。
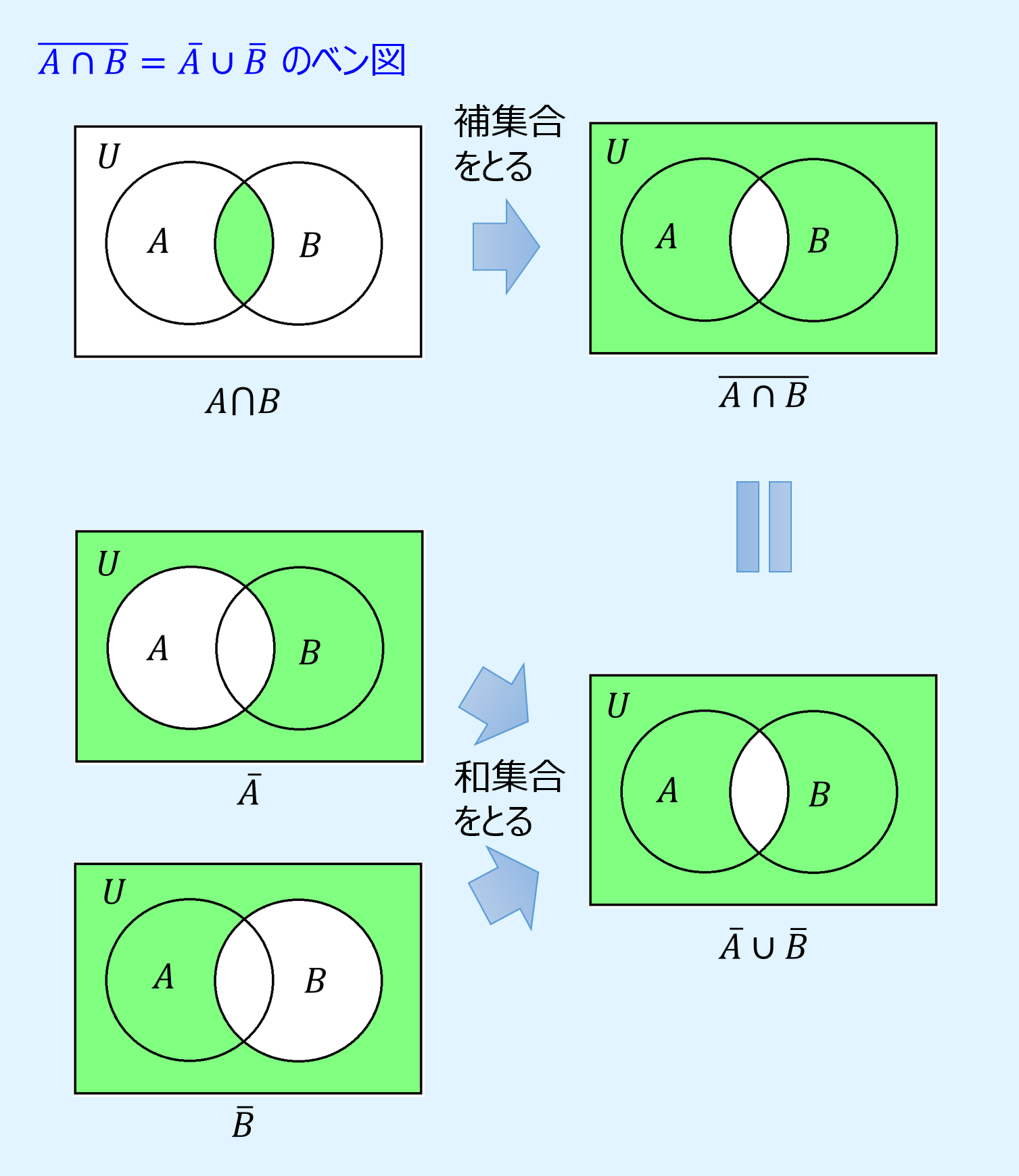
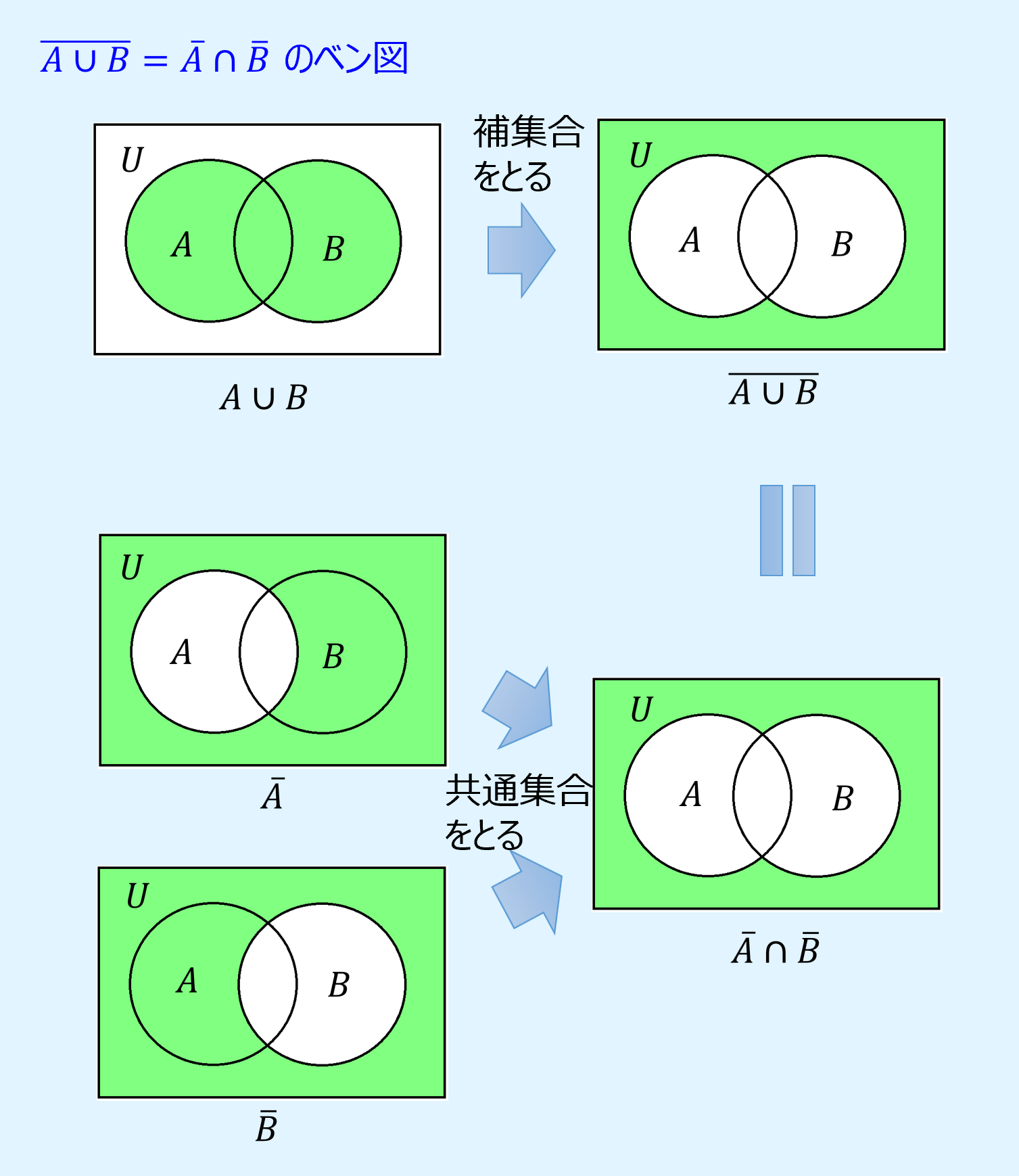
ド・モルガンの法則
ド・モルガンの法則(De Morgan’s laws)は、補集合をとる順番の前後を入れ替え、和集合と共通集合を入れ替えたものは等しいというもので、以下のように表されます。
ド・モルガンの法則は演算式の変換に頻繁に用いられますので、ぜひ覚えましょう。
また、ベン図でド・モルガンの法則を表すと以下のようになります。
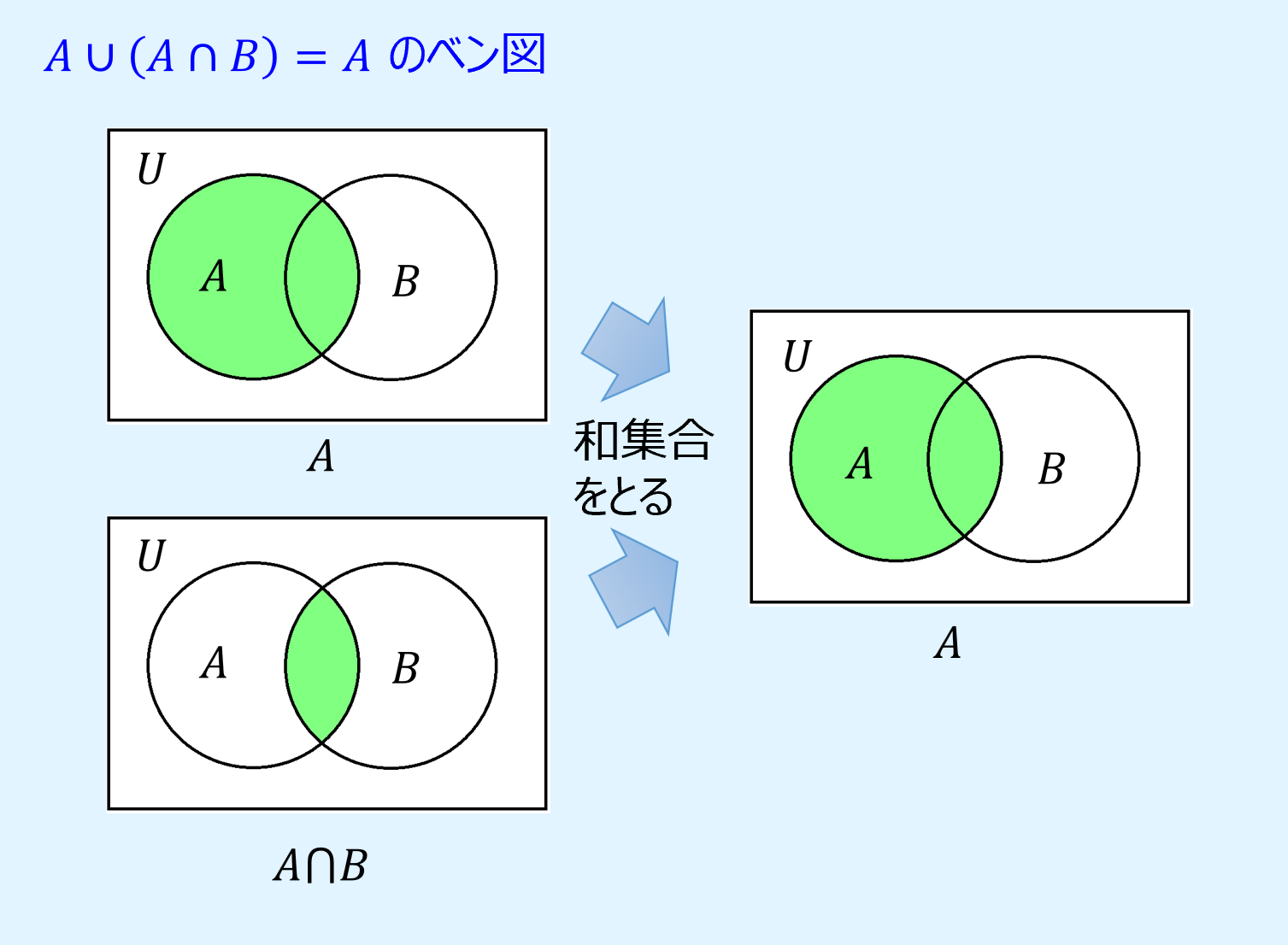
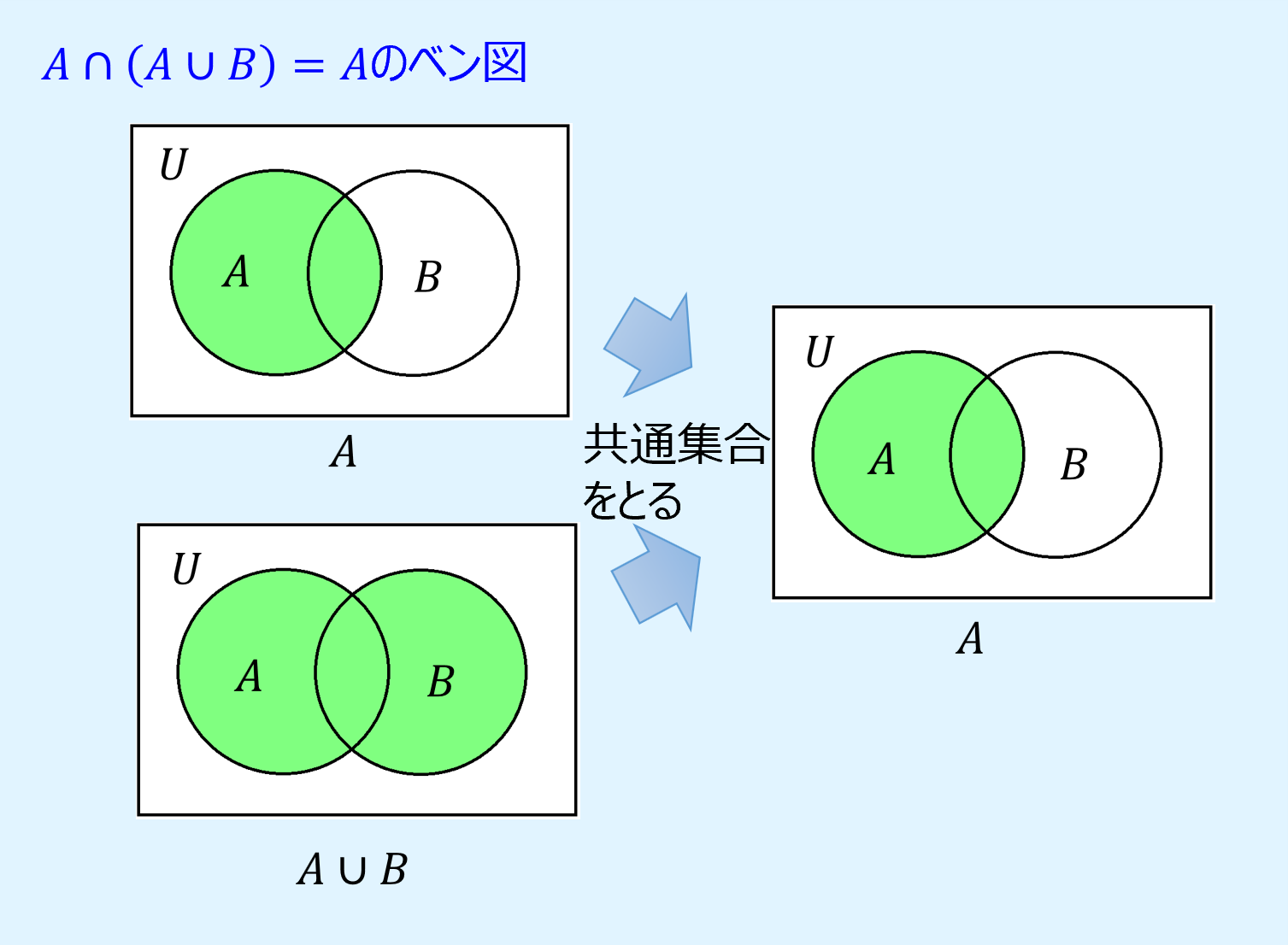
吸収則
吸収則(absorption laws)は、自身と他の集合の共通集合又は和集合を取ったものと自身の和集合または共通集合を取ると自身になるというもので、以下のように表されます。
また、ベン図で吸収則を表すと以下のようになります。
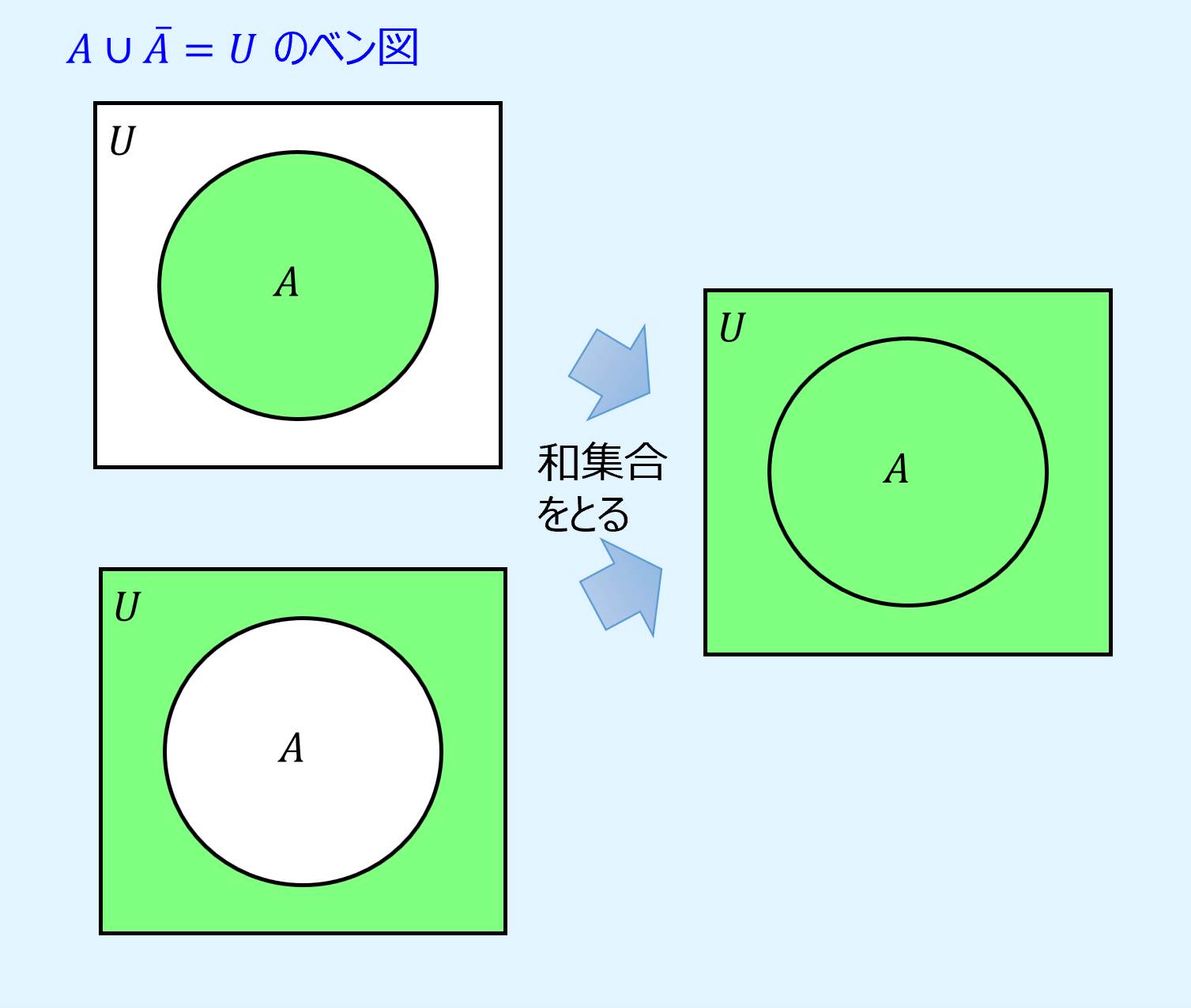
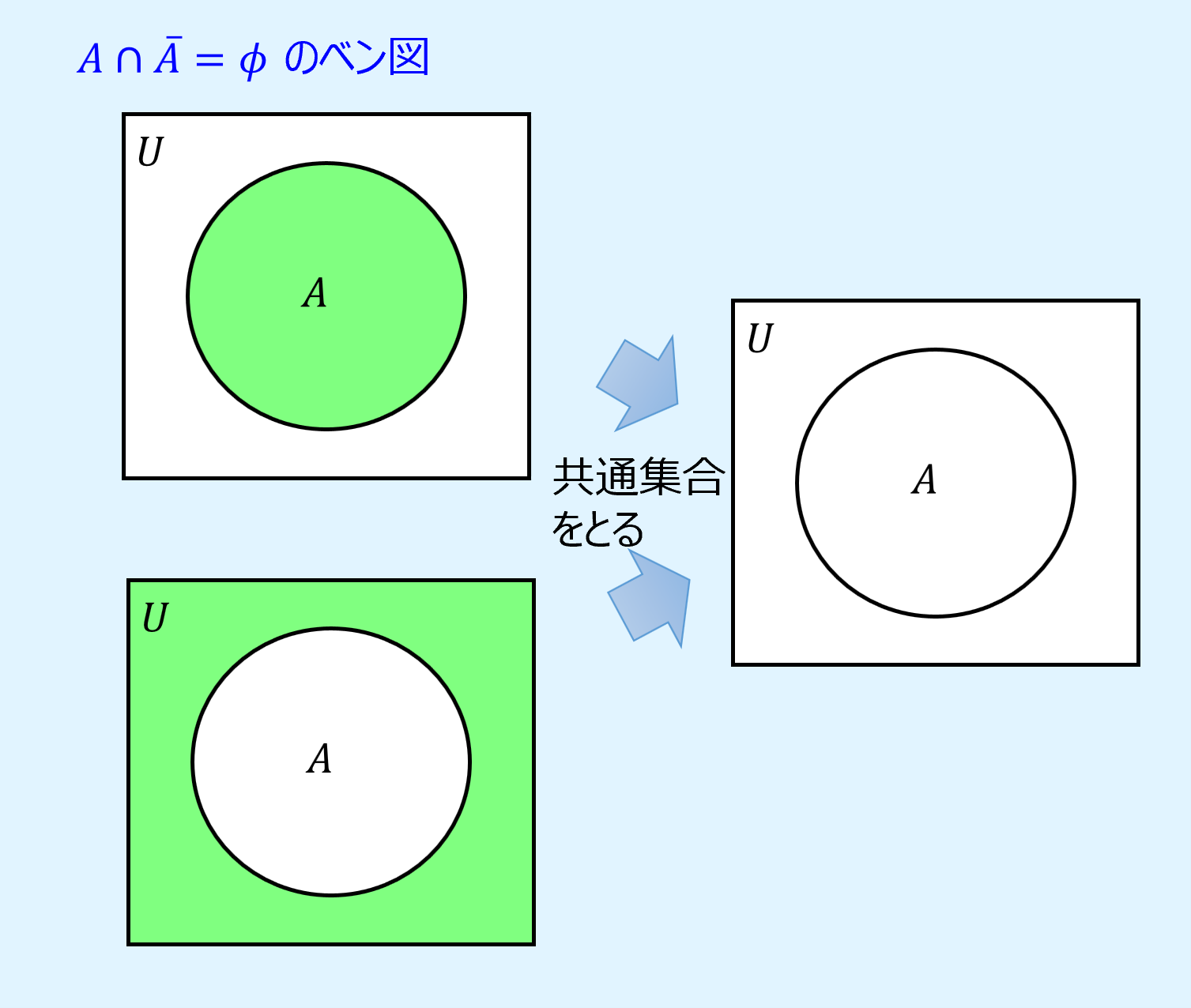
相補則
相補則(complementary laws)は、自身とその補集合の和集合は全体集合\(U\)になり、共通集合は空集合\(\phi\)になるというもので、以下のように表されます。
また、ベン図で相補則を表すと以下のようになります。

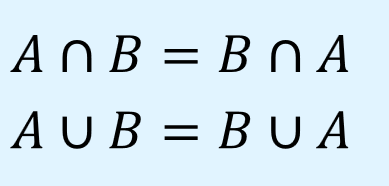
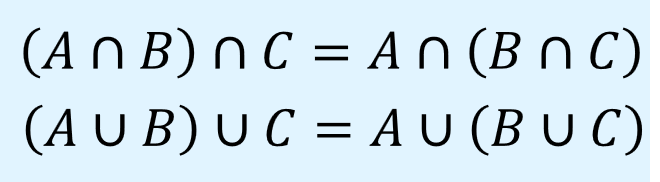
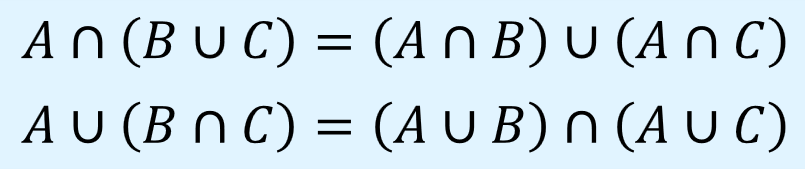
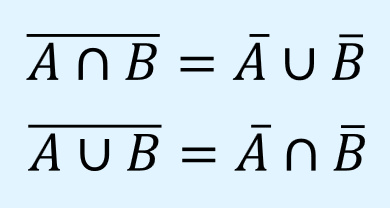
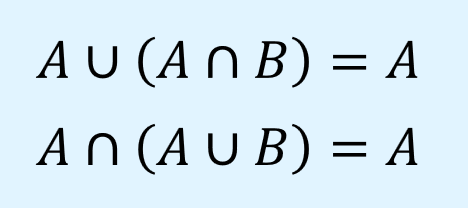
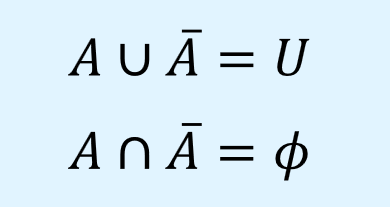


コメント