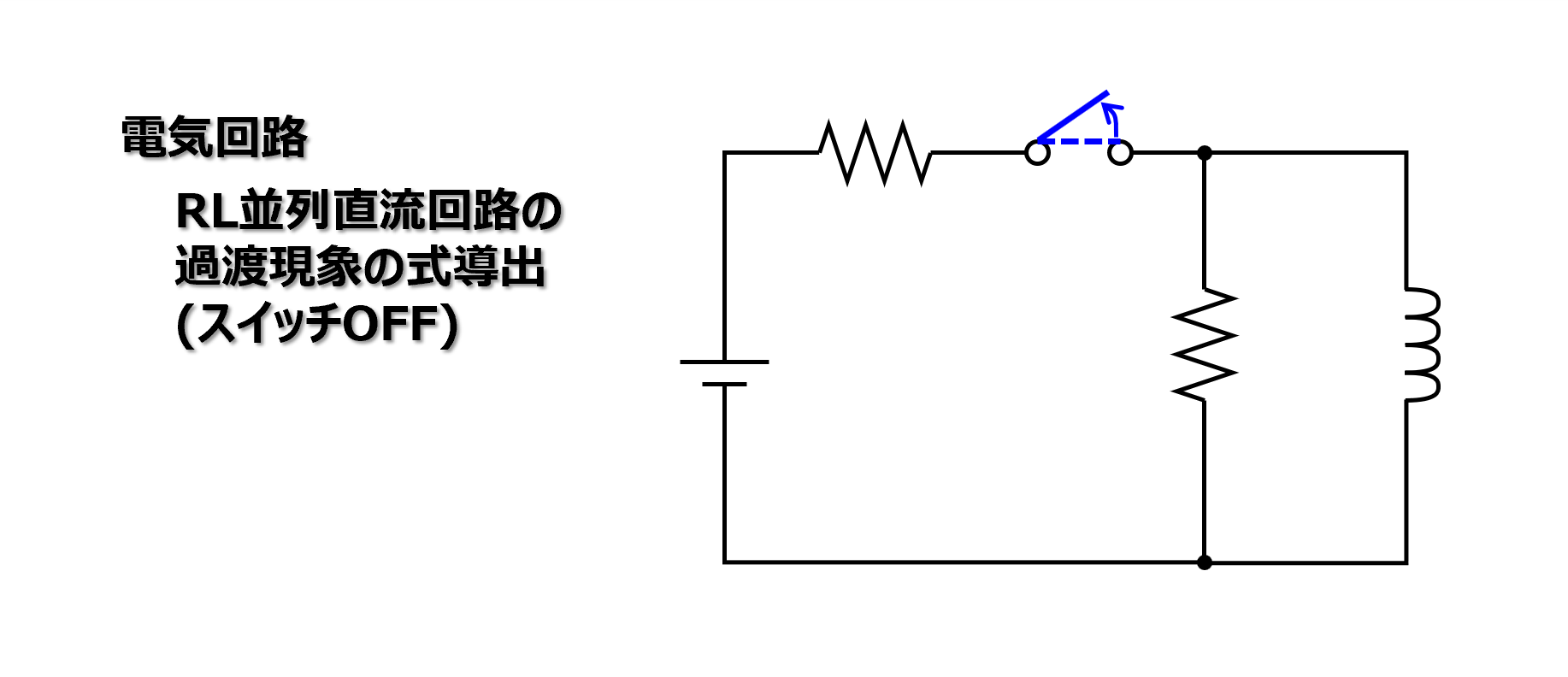
この記事では電気回路の一種であるRL並列回路の過渡現象について取り扱います。
抵抗とインダクタの並列接続から成る負荷と直流電源の間に設けられたスイッチをONからOFFにすることで過渡現象が生じます。過渡現象は電流と電圧の時間変化で表されますので、式導出をして求めます。
目次
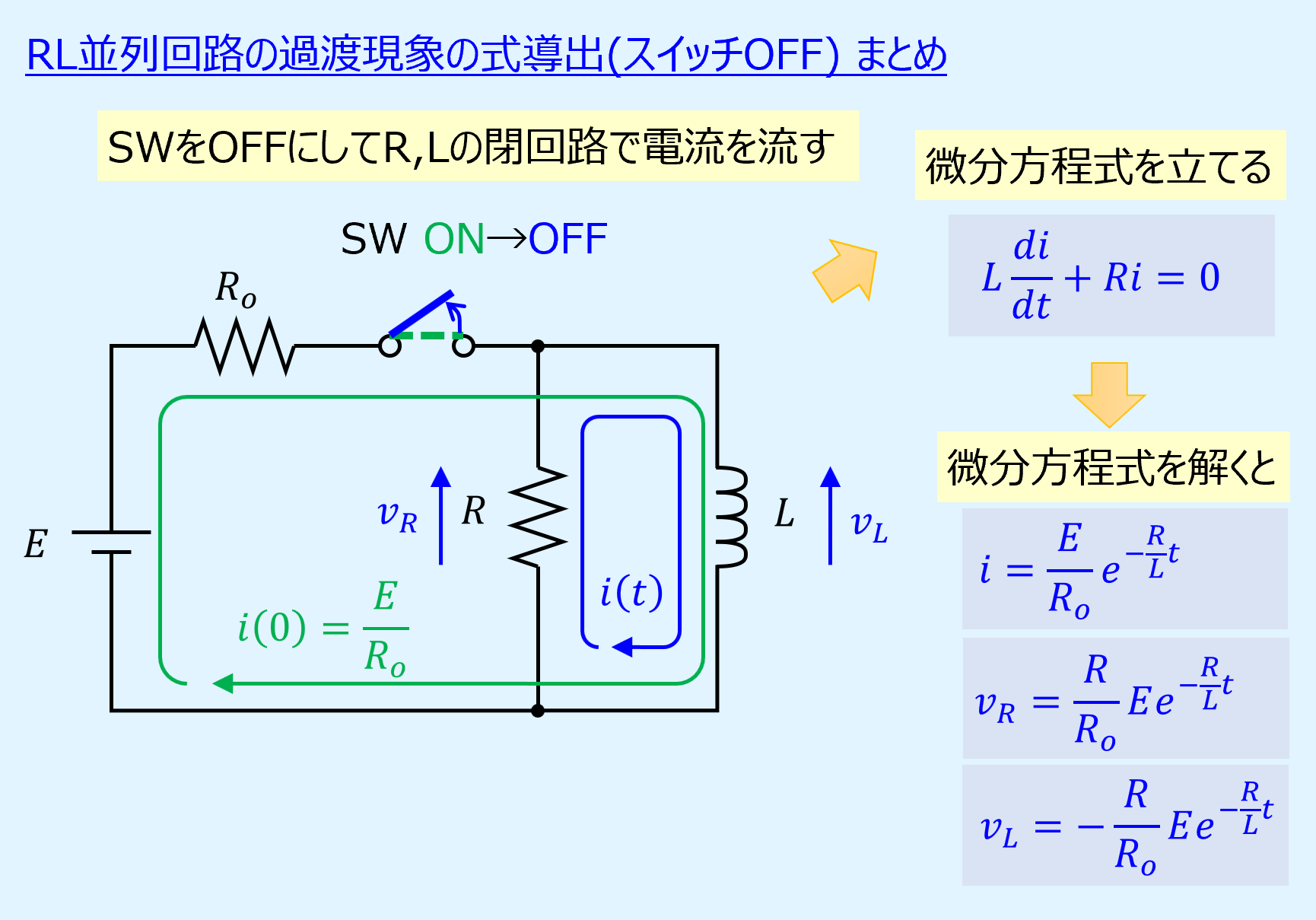
【まとめ】RL並列回路の過渡現象の式導出(スイッチOFF)
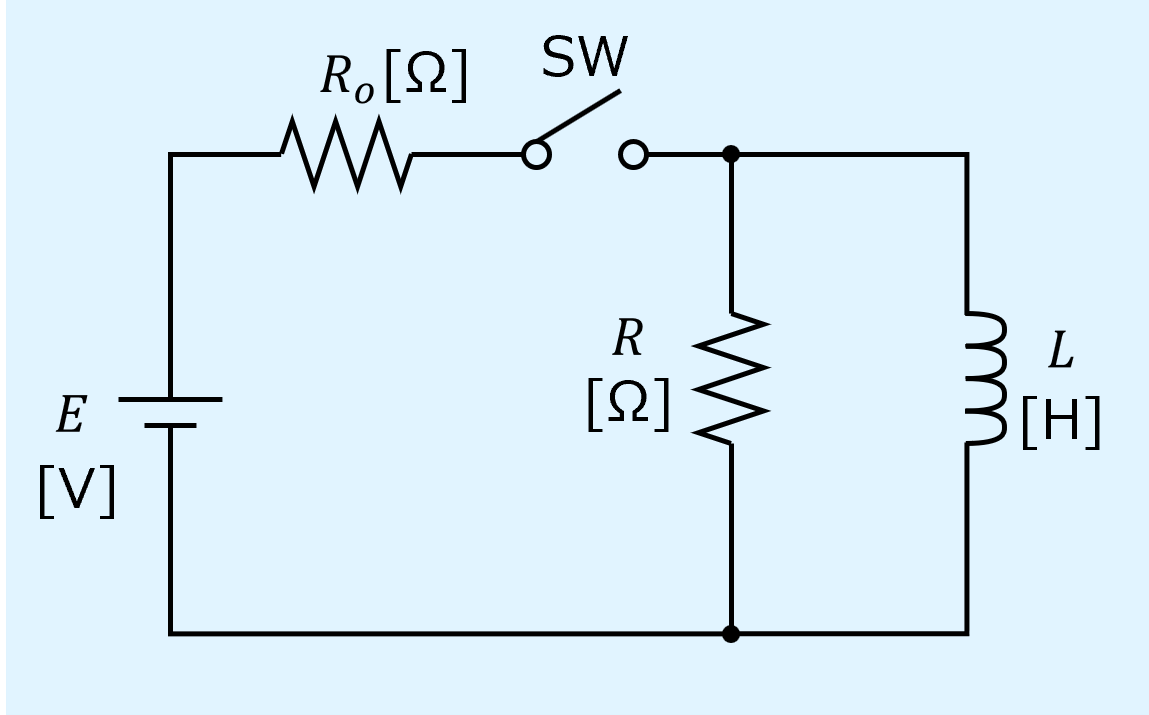
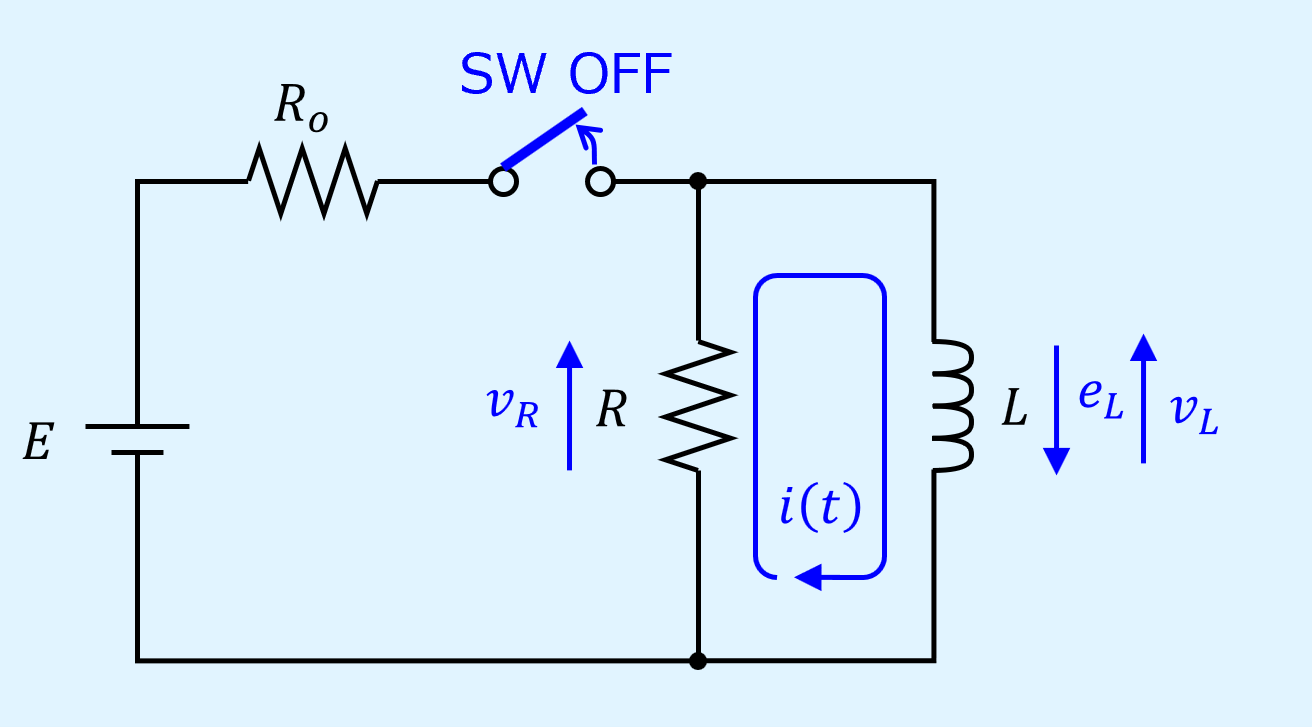
本記事での対象回路はRL並列回路で、抵抗とインダクタの並列接続から成る負荷に直流電源を接続したものです。
RLの負荷と抵抗の間にはスイッチSWを設けています。
このスイッチをOFFに切り替えることで生じる過渡現象について以降で説明を行います。
過渡現象の求め方
以下の順番で過渡現象を表す電流と電圧の値を求めます。
(1)初期状態の条件を求める。
(2)スイッチをOFFにした回路で微分方程式を立てる。
(3)解を仮定して微分方程式を解く。
(4)解の未定定数を初期状態から決定する。
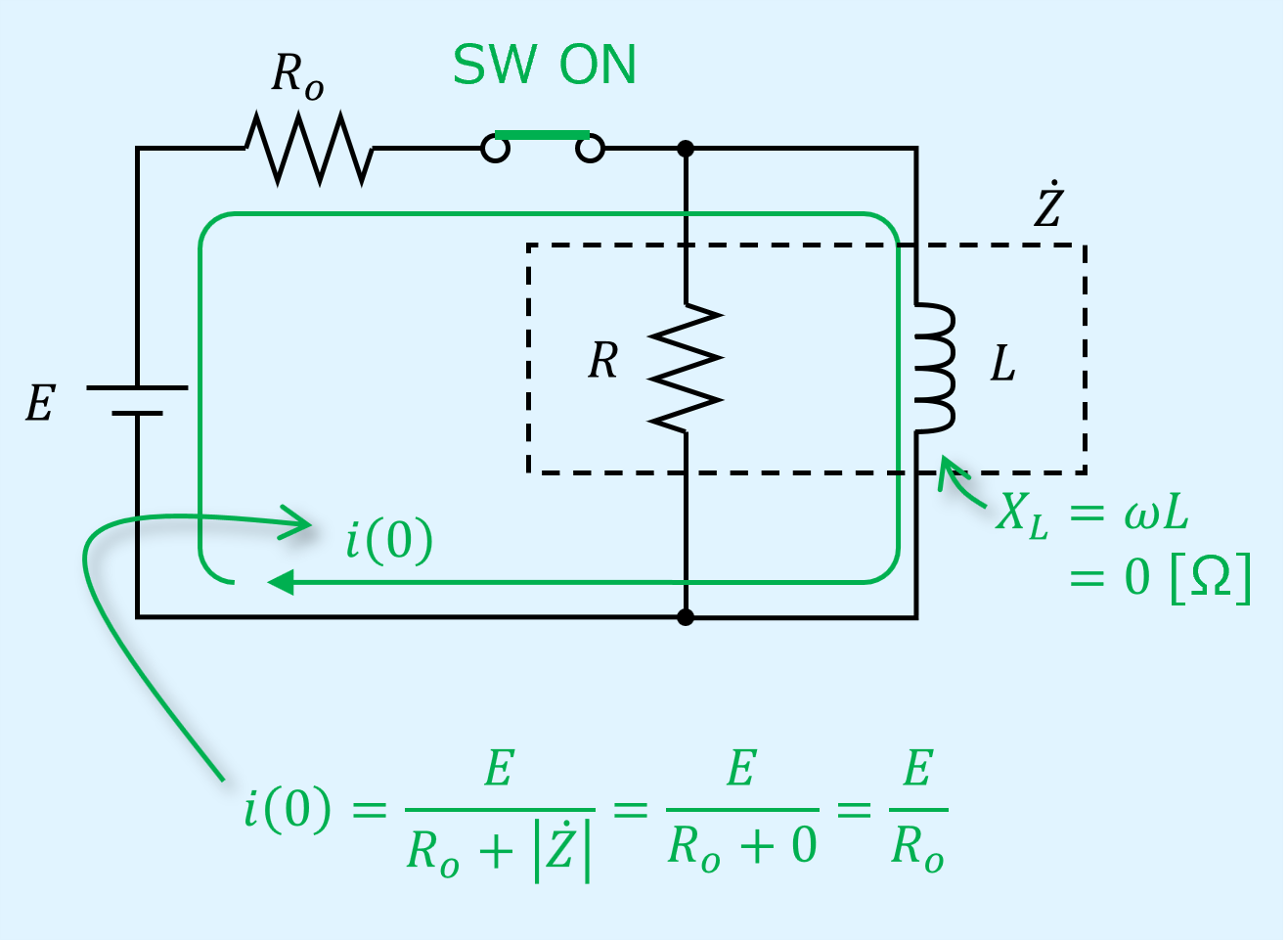
(1)初期状態の条件
初期状態ではRL並列回路のスイッチはONとなっています。
また、スイッチがONになってから十分に時間が経っているとします。
直流では角周波数\(\omega=0\)[Hz]であるため、インダクタLによるリアクタンスは\(X_L={\omega}L=0\)Ωとなります。
そのため抵抗Rには電流は流れず、インダクタLの経路にのみ電流\(i=E/R_o\)[A]が流れています。
次にスイッチをOFFにすると、インダクタは蓄えたエネルギーを放出して電流を流し続けようとします。
OFFにした直後の\(i\)はONのときと同じ\(E/R_o\)[A]です。
これが初期状態の条件です。
また、\(R_o\)は入れていないと電流が∞になるため、電流制限用に入れる必要があります。
(2)スイッチをOFFにした回路で微分方程式を立てる
RL並列回路のスイッチをOFFにすると過渡現象が起きます。
上記のRL並列回路に関して、キルヒホッフの第2法則(電圧則)、オームの法則、誘導起電力から、以下が得られます。
以上より\(i\)に関する微分方程式を立てることができます。
(3)解を仮定して微分方程式を解く
次に過渡現象の解を仮定してRL並列回路の微分方程式を解きます。
解とその微分を以下のように仮定します。
これを微分方程式に代入し、以下のように解くことができます。
式(5),(7)より\(i\)は、
未定定数\(A\)がまだ残っているので、次に\(A\)を求めていきます。
(4)解の未定定数を求める
過渡現象が始まる前の初期状態の条件より、未定定数\(A\)は以下となります。
求めた未定定数を代入すると、\(i\)は以下となります。
これがRL並列回路のスイッチをOFFにしたときの過渡現象を表す式となります。
また、指数関数中の\(-L/R\)は時定数と呼ばれ、記号\(\tau\)で表すこともあります。
時定数は定常状態に収束するまでに要する時間に関わり、小さければ収束が速く、大きければ収束が遅くなります。
過渡現象における電圧
RL並列回路のスイッチをOFFにしたときの抵抗の電圧は次式で表されます。
またインダクタの電圧は次式で表されます。
以上がRL並列回路のスイッチをOFFにしたときの過渡現象を表す式導出です。
その他
電気回路全般については以下をご覧下さい。
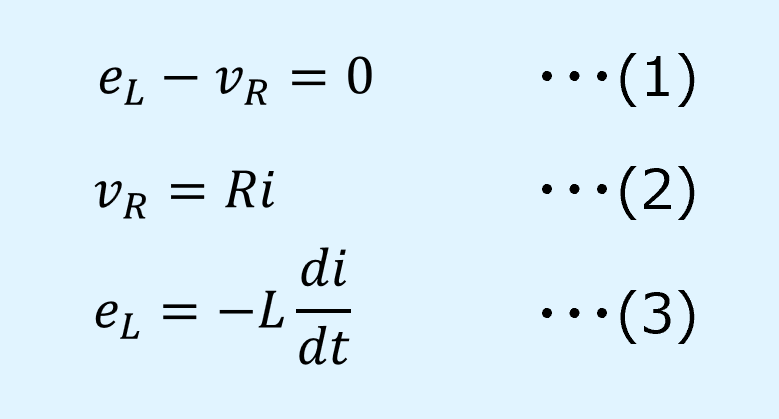
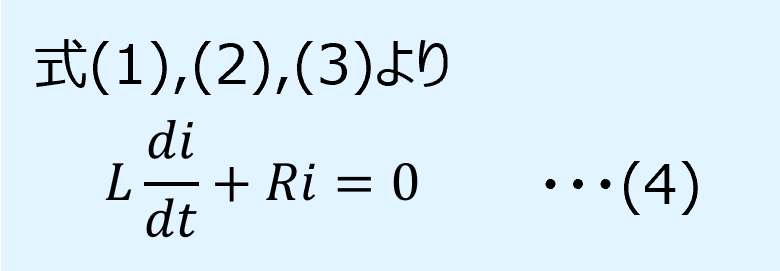
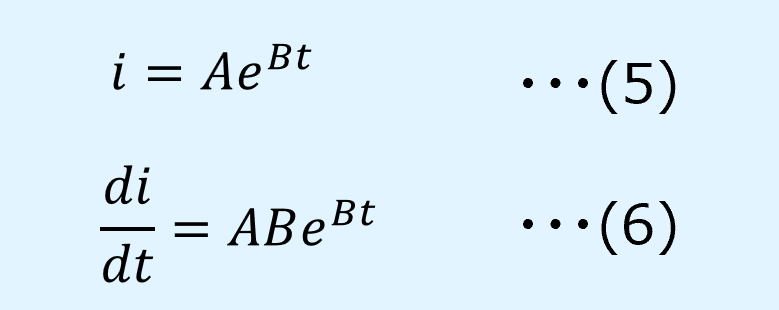

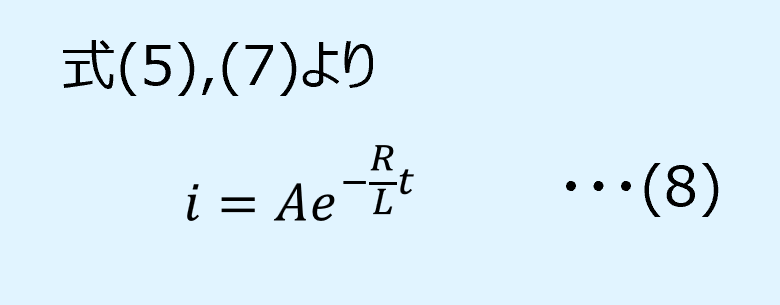

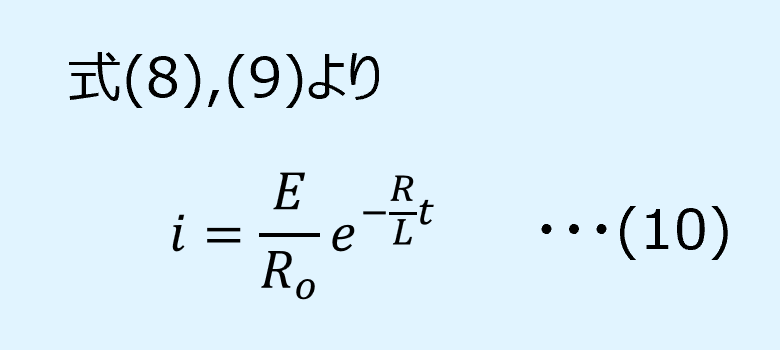
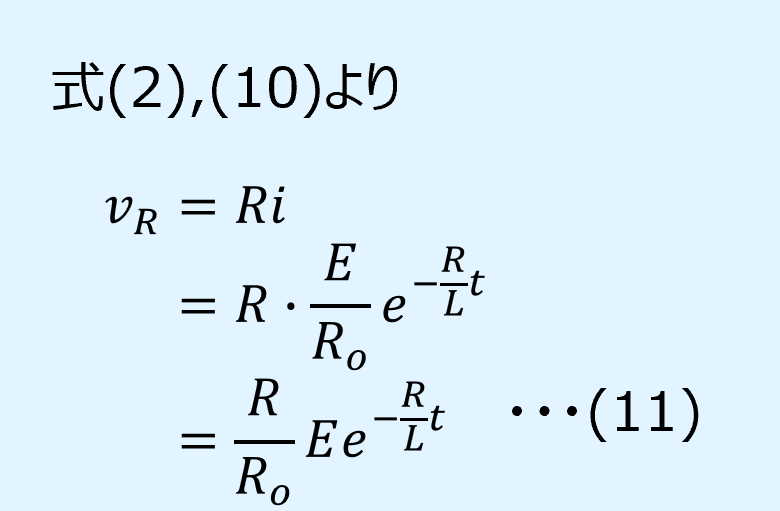
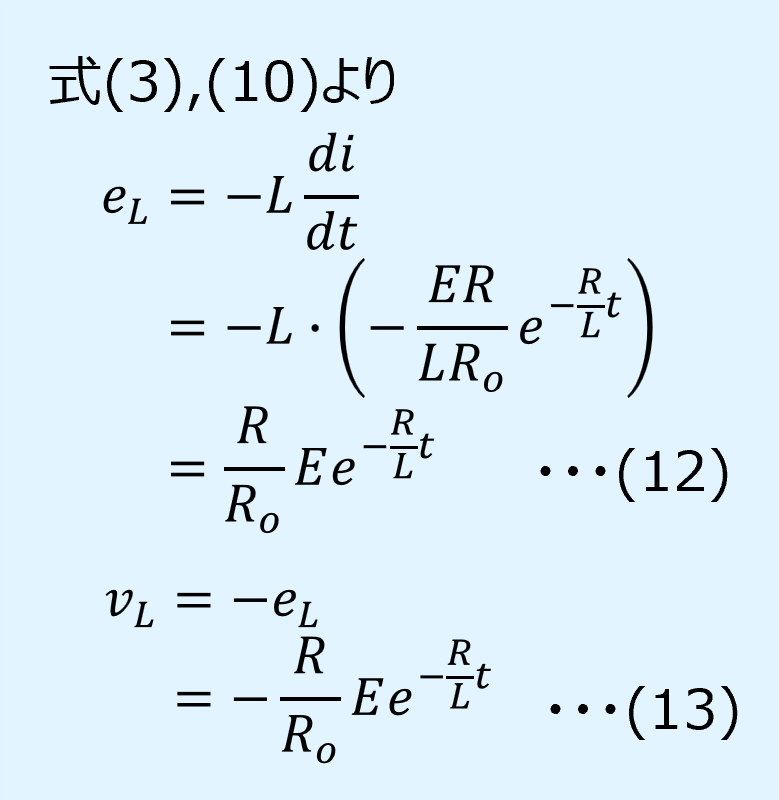


コメント