この記事では電気回路の一種であるRL直列回路の過渡現象について取り扱います。
RL直列回路のスイッチをONにした後の電流、電圧値がどうなるのか、その傾向についてグラフを用いて説明します。
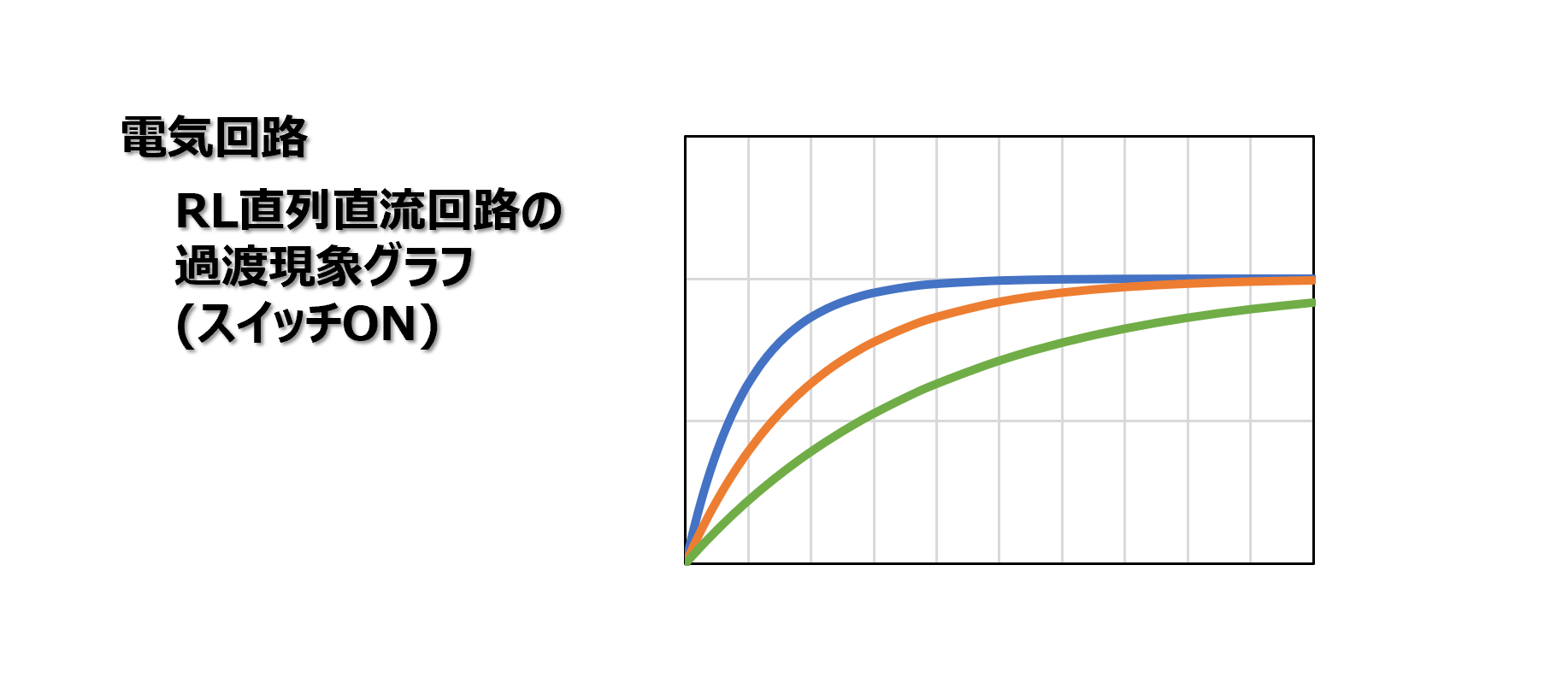
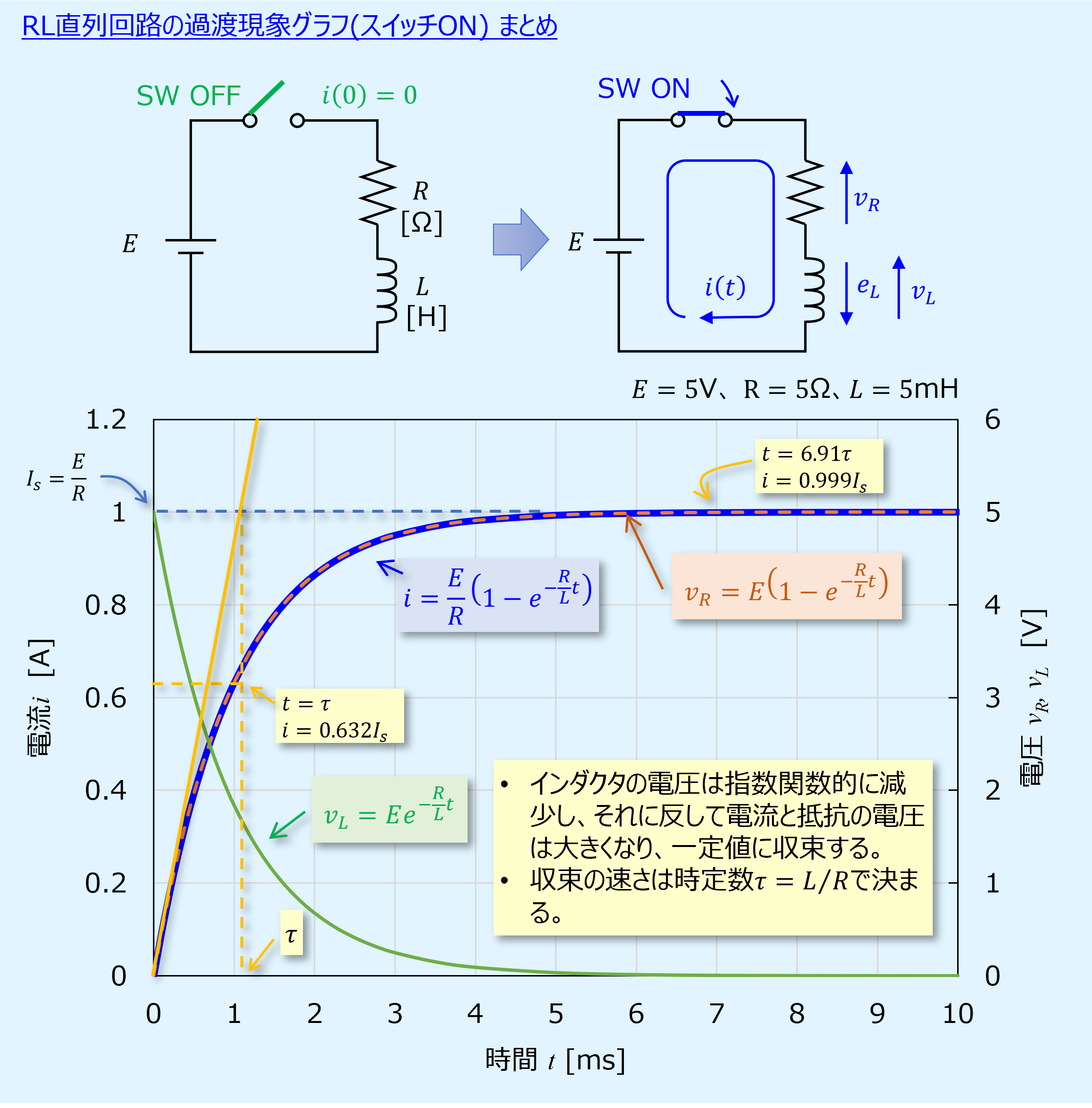
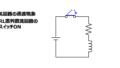
【まとめ】RL直列回路の過渡現象グラフ(スイッチON)
RL直列回路の過渡現象
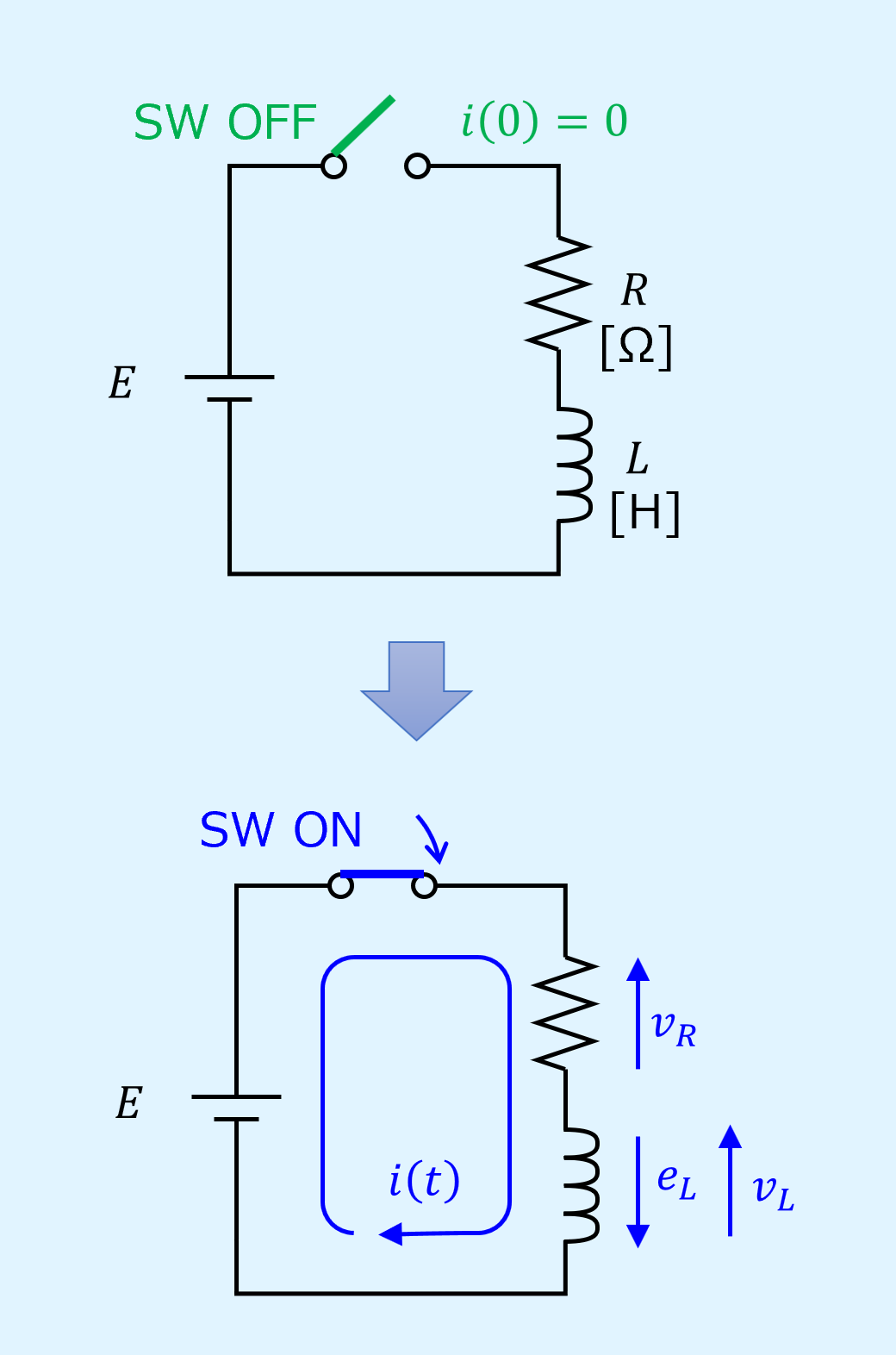
RL直列回路のスイッチをONにすると、インダクタの誘導起電力により、電流は直ぐに大きくならず、徐々に大きくなっていきます。
これがRL直列回路のスイッチをONにした時に生じる過渡現象です。
RL直列回路のスイッチをONにした時の過渡現象における電流と電圧の式は以前の記事で導出しました。
本記事では導出した式をグラフにして過渡現象を視覚的に説明します。
電流のグラフ
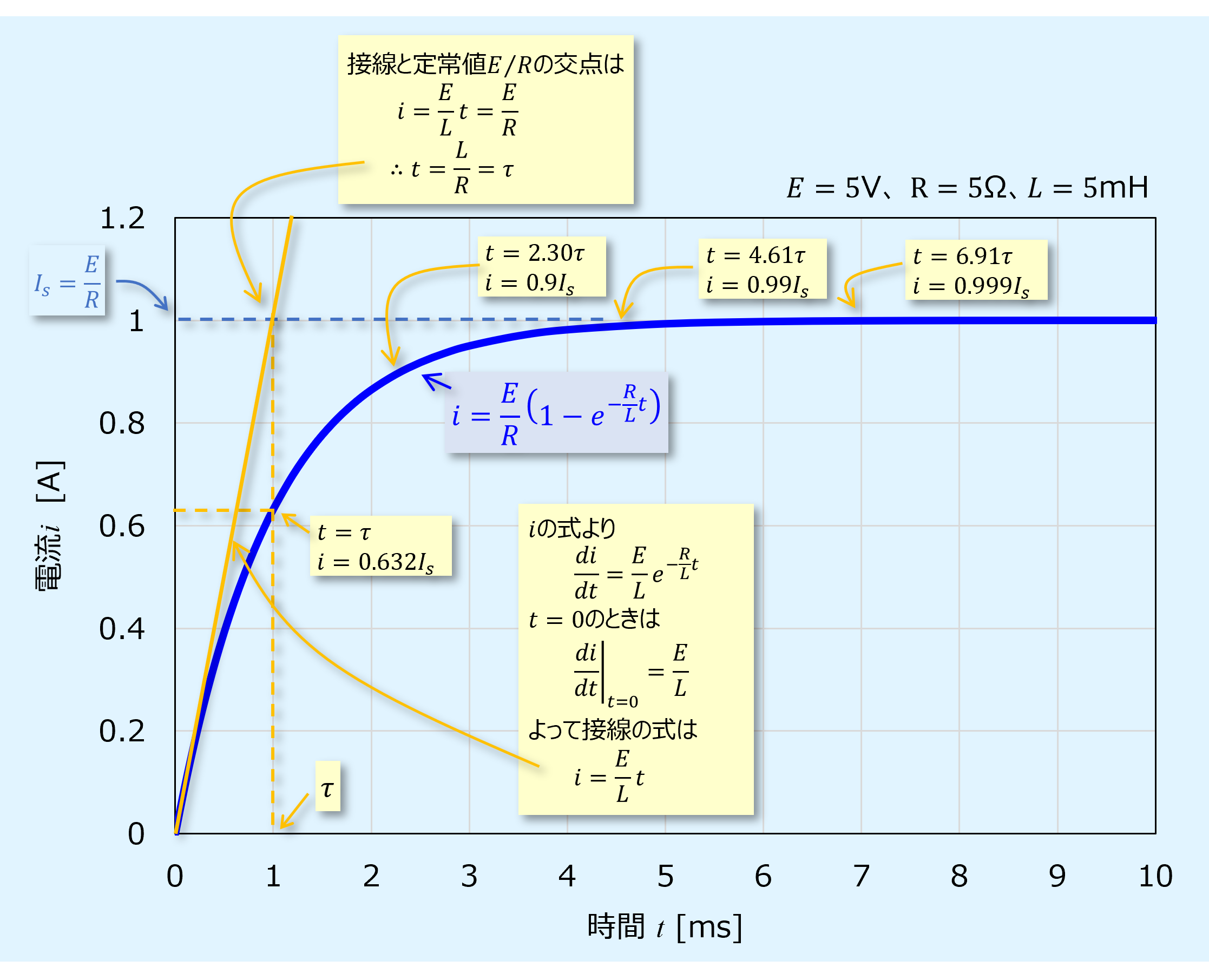
RL直列回路のスイッチをONにした時の過渡現象における電流の式は以下の通りです。
この式よりグラフは以下となります。
スイッチをONにした直後、初期状態の\(i\)は0[A]です。
そこから増加していきますが、途中から増加量は減り、定常状態である\(E/R\)[A]へなだらかに収束していきます。
収束に要する時間は時定数\(\tau=L/R\)[ms]に依存します。
感覚的に時定数の影響が分かるように、時間軸上に時定数が記載されていることがあります。
これはスイッチをONにした\(t=0\)のときの接線が定常状態の値となる時間が\(\tau\)となるためです。
\(t=\tau\)のときの\(i\)は、中途半端ですが、定常状態の0.632倍になります。
定常状態がどこからか、という厳密な定義はありません。
しかし、有効桁数3桁で観測をしているなら、定常状態の0.999倍となる\(t≒6.91\tau\)以降ですと測定結果に変化が無くなるため定常状態といって差し支えありません。
なお、定常値の0.9倍となるのは\(t≒2.30\tau\)、0.99倍だと\(t≒4.61\tau\)です。
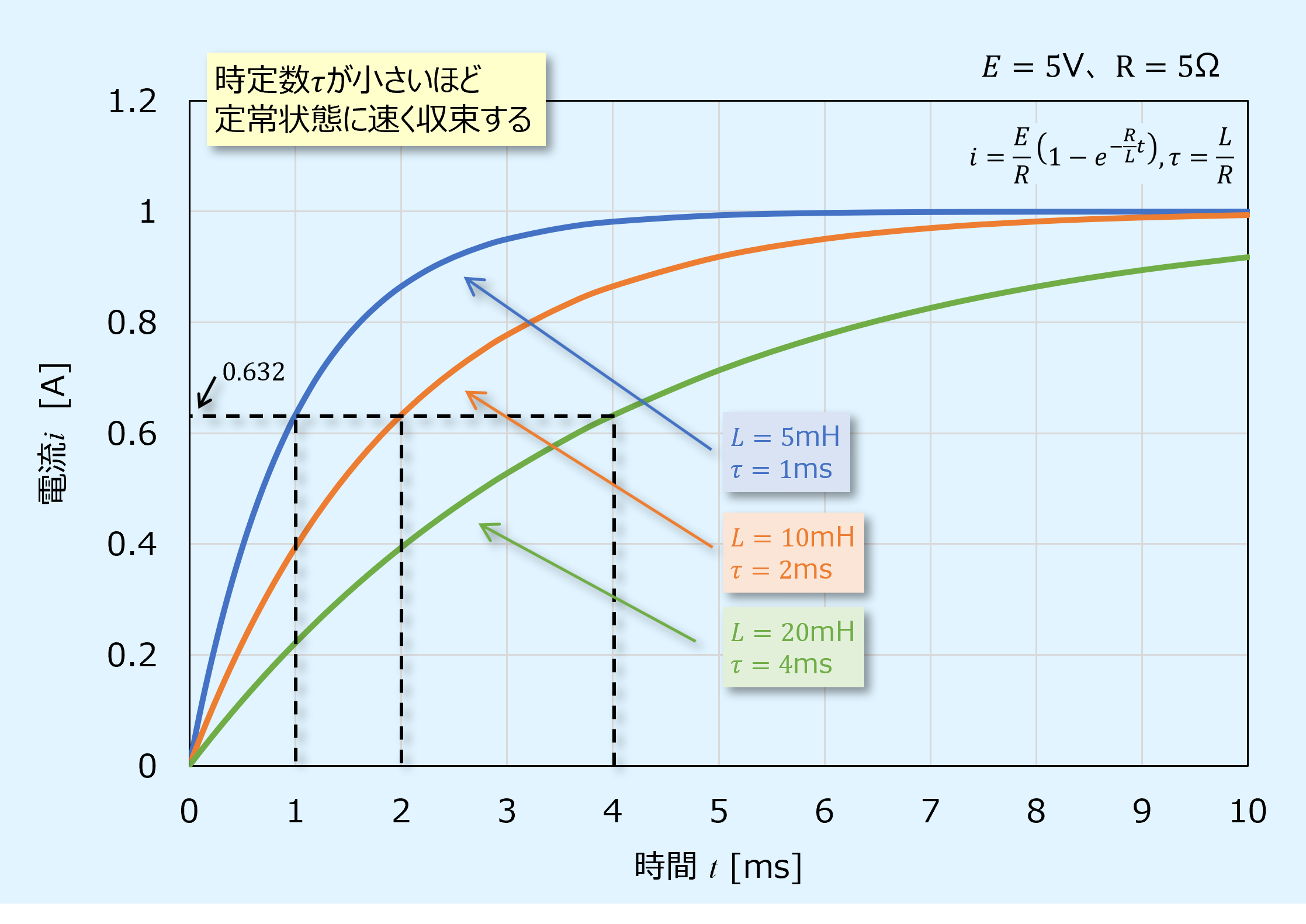
時定数の影響を見るために、インダクタンスを変更した場合のグラフを以下に示します。
速くONへ切り替えるためには時定数を小さくするしかありません。
そのためには抵抗を大きくするか、インダクタンスを小さくするかの2択となります。
しかし、直列抵抗を大きくすると、その分電力を無駄に消費したりしますので現実的ではありません。
代わりにインダクタンスの値で時定数を調整します。
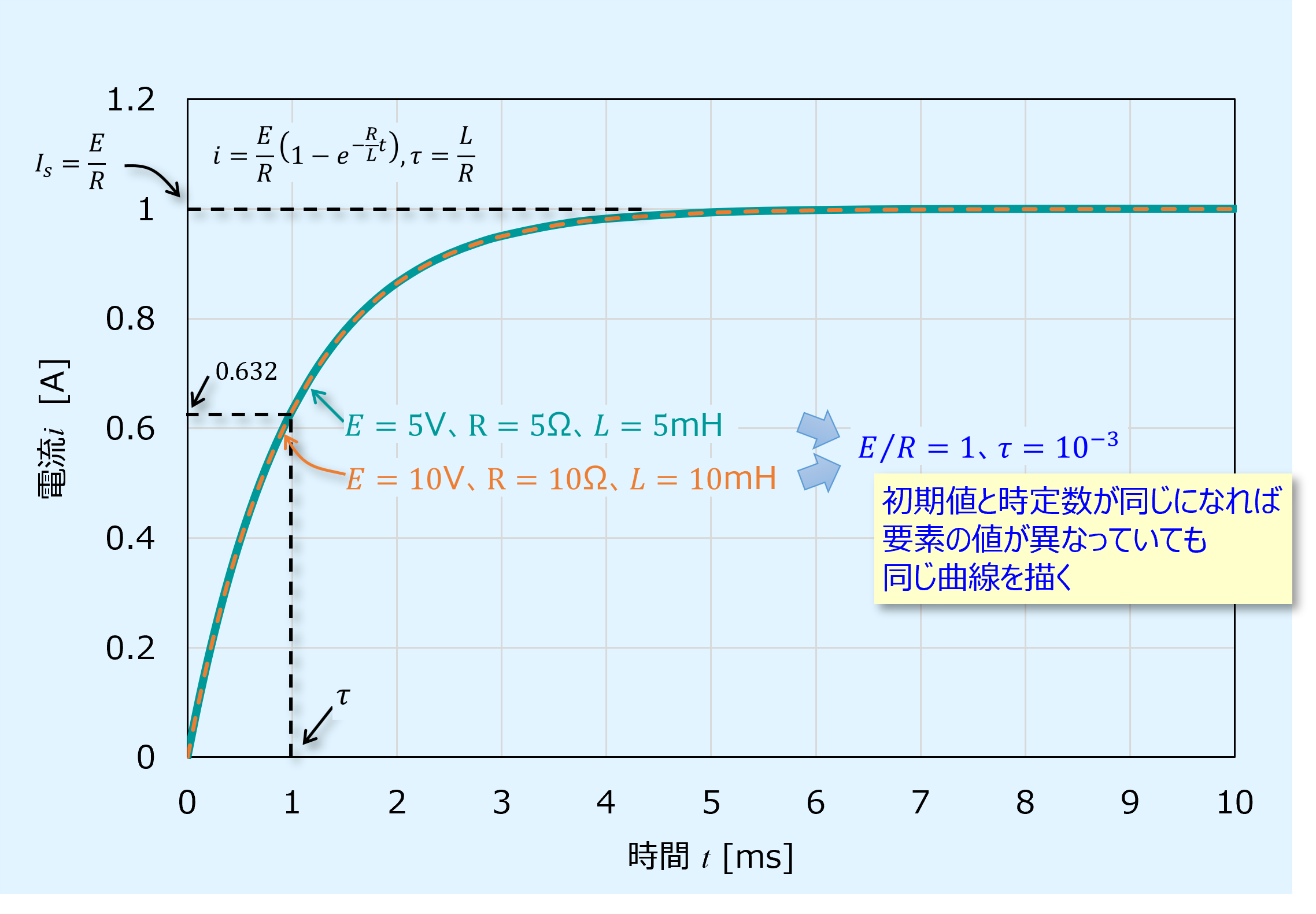
要素の電源電圧、抵抗、インダクタンスが異なっていても、定常値、時定数が同じになれば過渡現象は同じになります。
10V、10Ω、10mHの例を上記のグラフに合わせて記載します。
電圧のグラフ
RL直列回路のスイッチをONにした時の過渡現象における抵抗とインダクタ両端の電圧は次式で表されます。
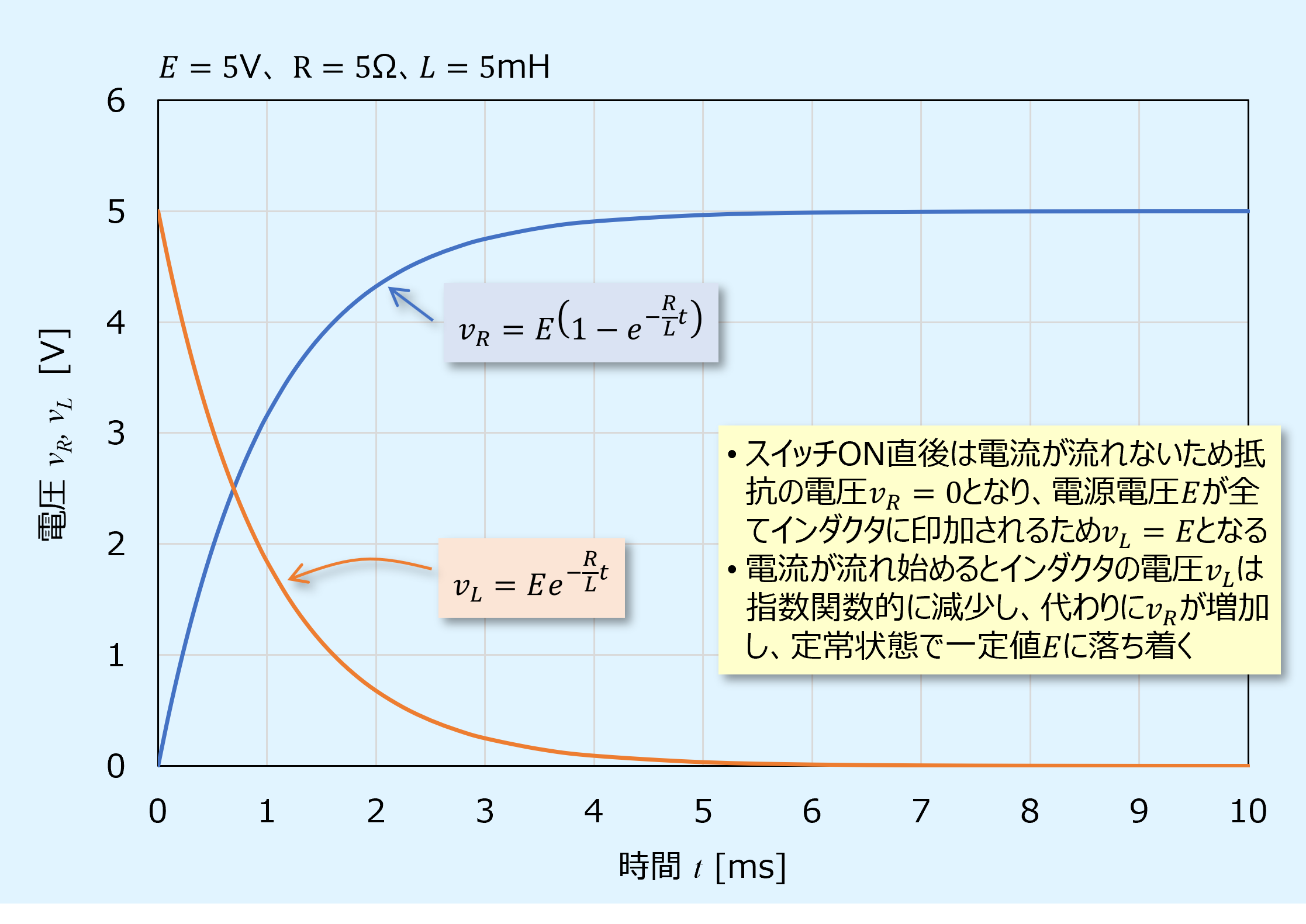
上式より抵抗とインダクタ両端の電圧のグラフは以下となります。
\(t=0\)において電源電圧\(E\)は全てインダクタに加わるため、\(v_L=E\)、\(v_R=0\)となっています。
その後、インダクタの電圧は指数関数的に減少し、代わりに抵抗の電圧が増加していきます。
電源電圧が5Vだと、CMOSのHighレベルである3.5V以上になるのは\(t≒1.2\tau\)のとき、TTLのHighレベルである2V以上だと\(t≒0.5\tau\)です。
グラフの条件ですと\(\tau=1\)[ms]ですので、\(t=1.2\)msのときに3.5V、\(t=1.8\)msのときに2Vとなります
その他
電気回路全般については以下をご覧下さい。



コメント