この記事では電気回路の一種であるRLC並列回路について説明をします。
電圧を基準とした場合に、電流の振幅、位相がどうなるのかを求めます。
【まとめ】RLC並列回路
RLC並列回路
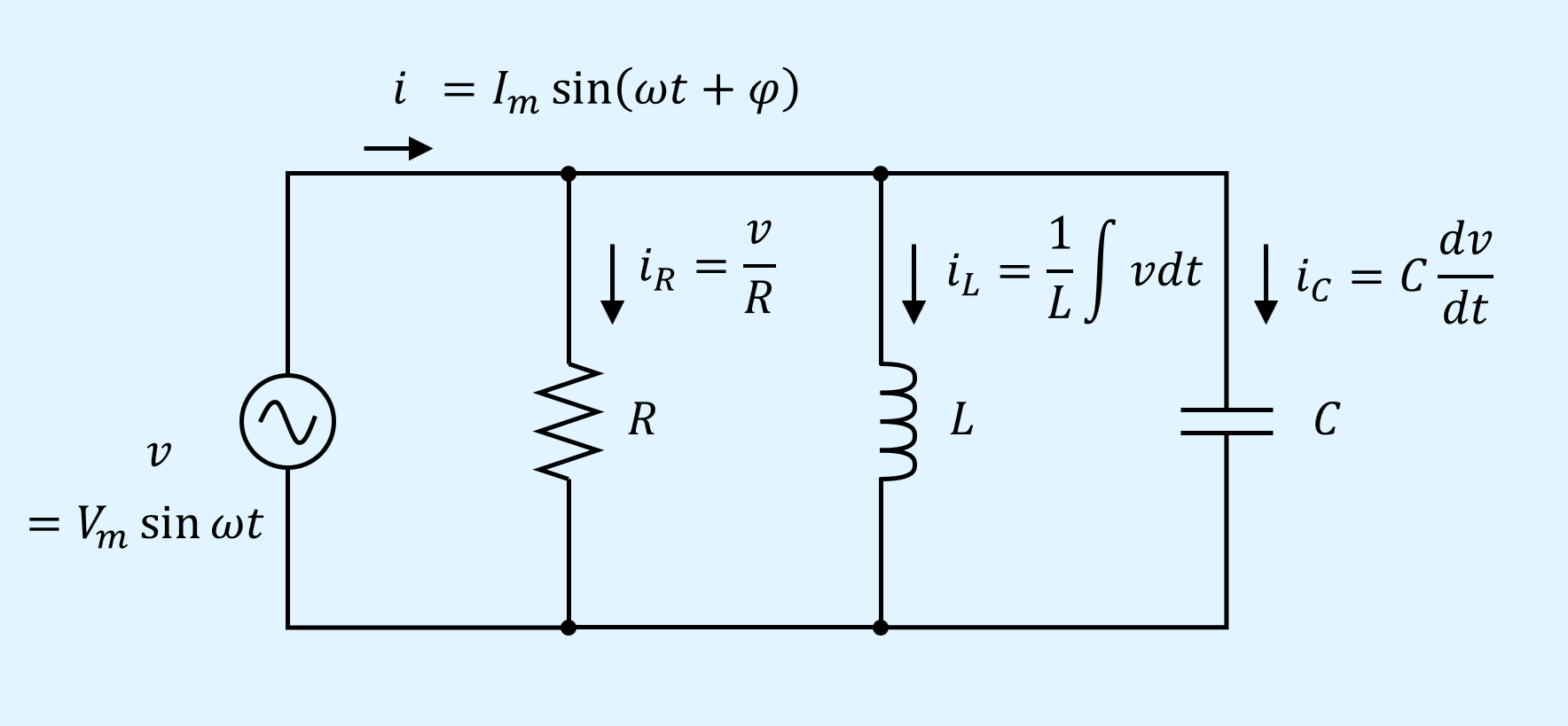
抵抗\(R\)、インダクタンス\(L\)、キャパシタンス\(C\)を並列に接続したRLC並列回路を以下に示します。
電源として交流電源を接続しています。
\(i_R\)、\(i_L\)、\(i_C\)はそれぞれ電圧\(v\)によって抵抗、インダクタ、キャパシタンスに流れる電流です。
並列回路は電圧を基準にした方が分かりやすいため、電圧\(v\)の位相は0とし、電流\(i\)の位相を電圧との相対位相\(\varphi\)としています。
以降で、電圧を基準とした場合の電流の振幅\(I_m\)、位相\(\varphi\)を求めます。
微分方程式を解いて振幅、位相を求める
キルヒホッフの第1法則(電流則)より、以下が成り立ちます。
よって、
上式を微分すると、電圧\(v\)に関する微分方程式となります。
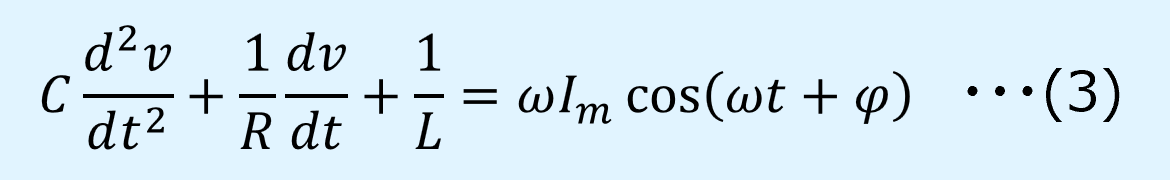
電圧\(v\)、及びその1階微分と2階微分は以下となります。
式(4),(5),(6)を式(3)に代入すると以下となります。
式(7)をsin項についてまとめると、以下が得られます。
式(7)をcos項についてまとめると、以下が得られます。
式(8)を式(9)で割り、逆正接を取ると、電流の位相\(\varphi\)が求まります。
ここで、\(B\)はサセプタンス、\(G\)はコンダクタンスを表しています。
式(8)、(9)の両辺を2乗すると、
式(11)、(12)を加算すると
よって
平方根を取ると、電流の最大振幅\(I_m\)となります。
ここで、\(\dot{Y}\)はアドミタンスを表しています。
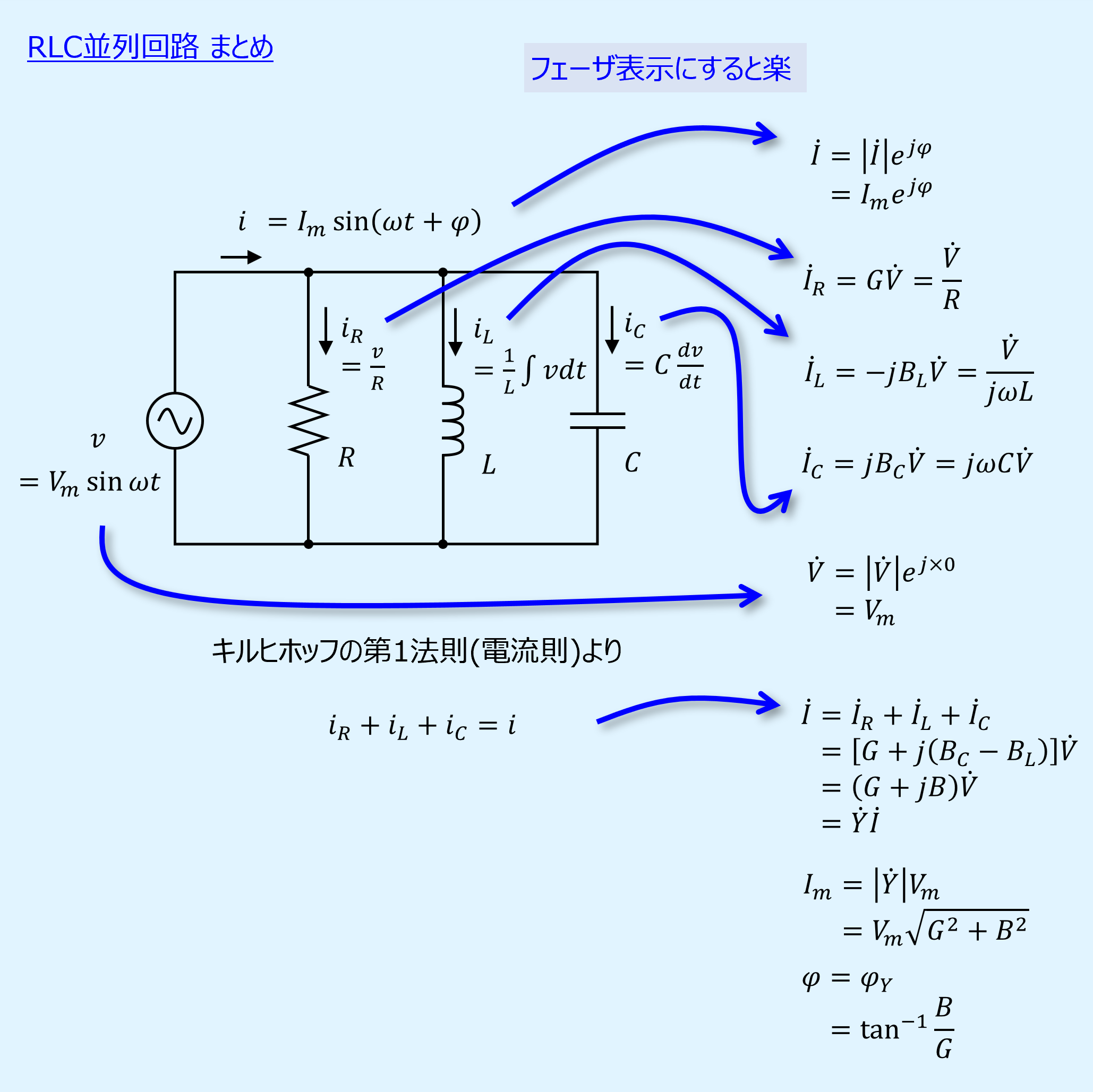
フェーザ表示より振幅、位相を求める
次に、フェーザ表示から電流の最大振幅\(I_m\)と位相\(\varphi\)を求めます。
フェーザを用いた方が簡単なので、通常こちらが用いられます。
\(i_R\)、\(i_L\)、\(i_C\)のフェーザは以下の通り。
ここで、位相関係は、\(\dot{I}_R\)は電圧と同相、\(\dot{I}_L\)は電圧より\(\pi/2\)位相が遅れており、\(\dot{I}_C\)は\(\pi/2\)位相が進んでいる、となっています。
式(1)に上式のフェーザを適用すると
アドミタンスのフェーザ\(\dot{Y}\)の極座標表示は以下の通り。
また、電圧のフェーザ\(\dot{V}\)の極座標表示は以下の通り。
式(18)、(21)を式(17)に代入すると、
電流のフェーザの大きさ\(|\dot{I}|\)及び最大振幅\(I_m\)は、式(19)、(22)より、以下となります。
電流の位相\(\varphi\)は式(20)、(22)より、以下となります。
式(23)、(24)は微分方程式を解いて求めた式(13)、(10)と同じであり、フェーザ表示での計算でも結果が同じになることが分かります。
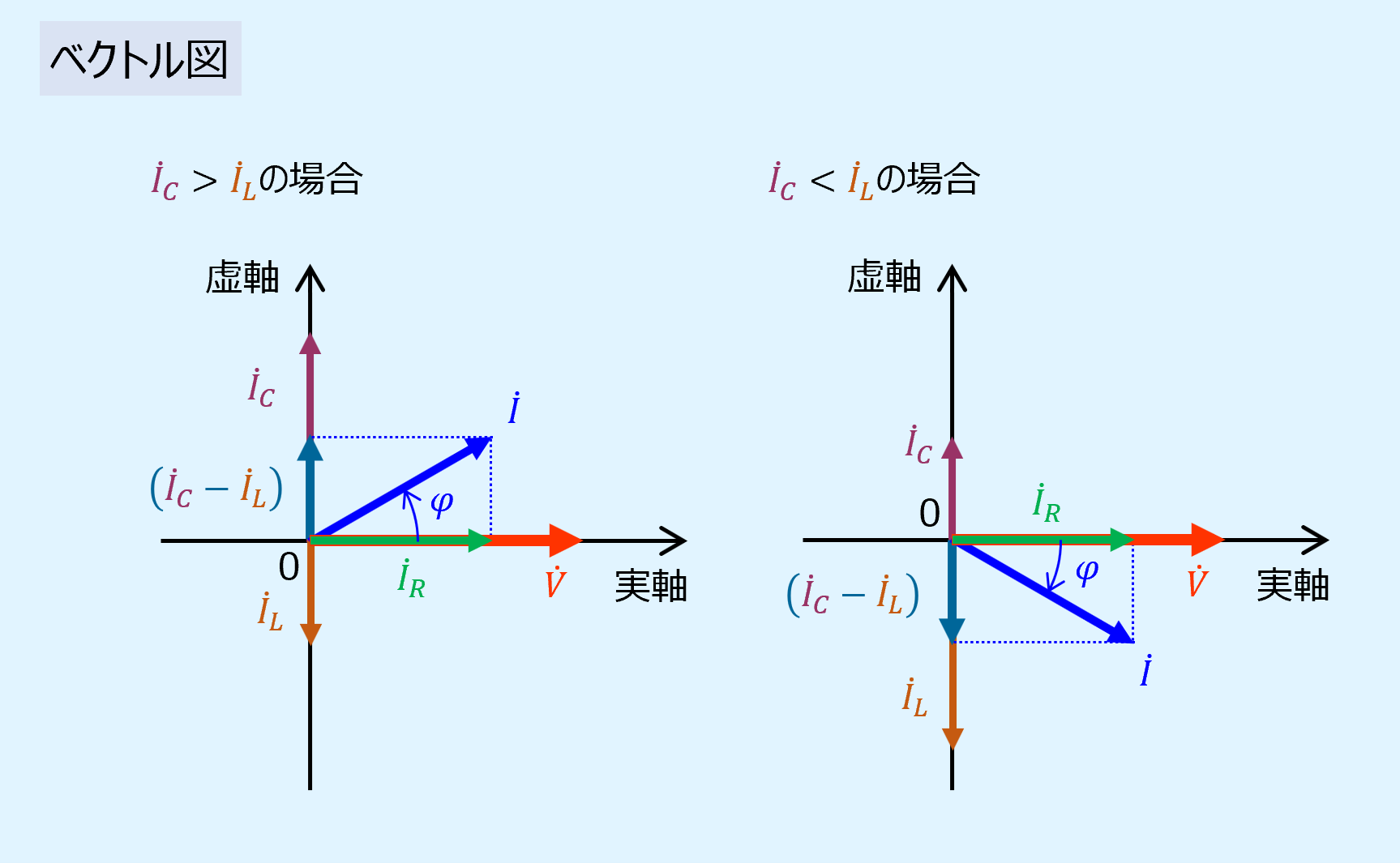
ベクトル図
フェーザをベクトル図示したものを以下に示します。
容量性の\(\dot{I}_C\)の方が大きければ回路全体の電流\(\dot{I}\)は時計方向に、誘導性の\(\dot{I}_L\)の方が大きければ\(\dot{I}\)は反時計方向に回ります。
その他
電気回路全般については以下をご覧下さい。
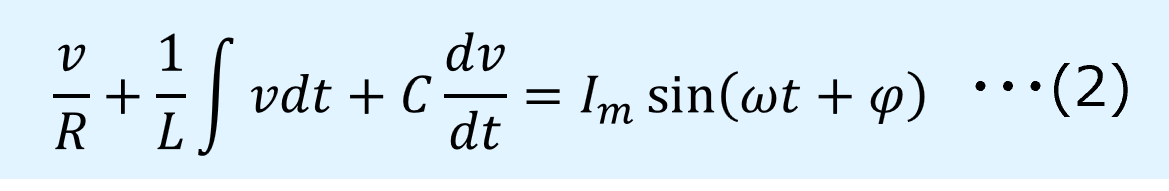
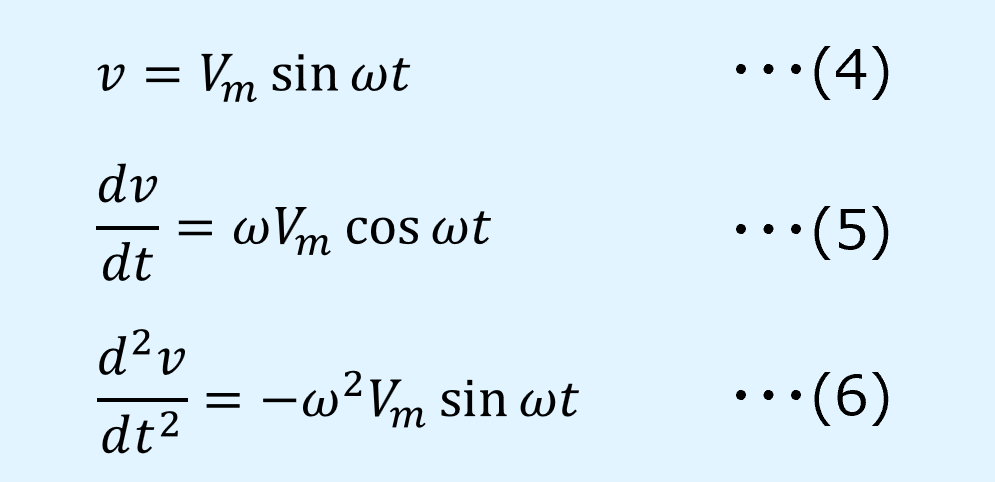
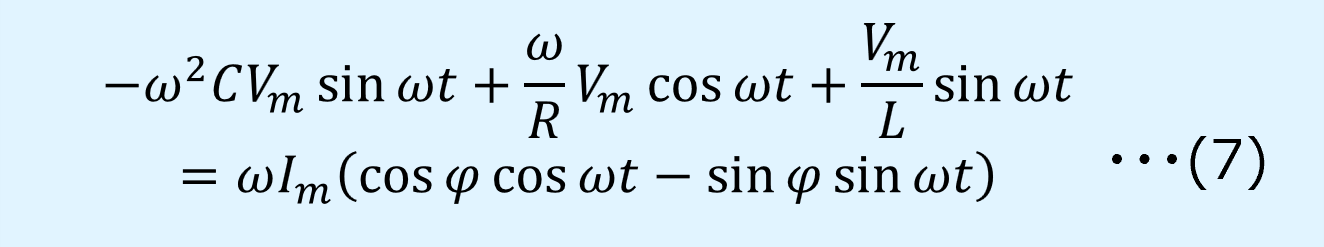
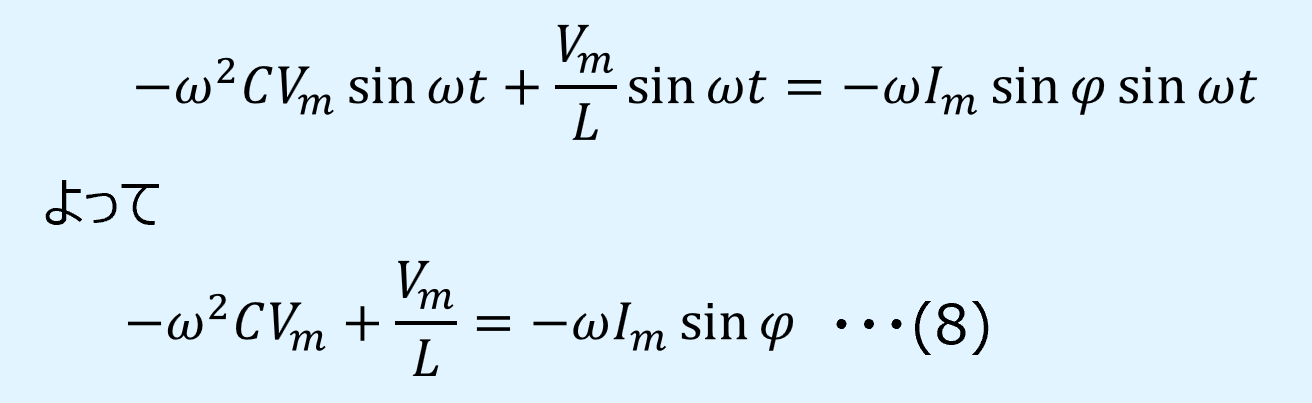
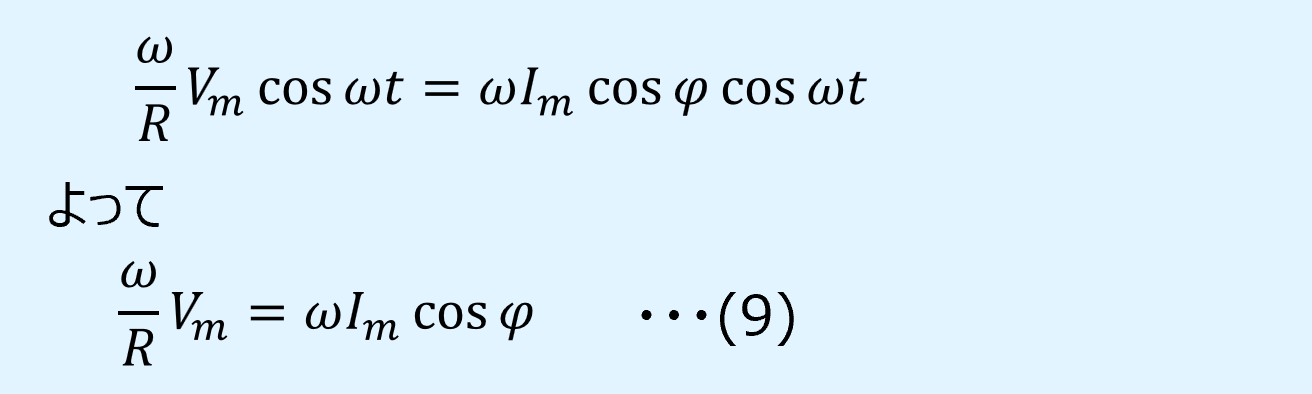
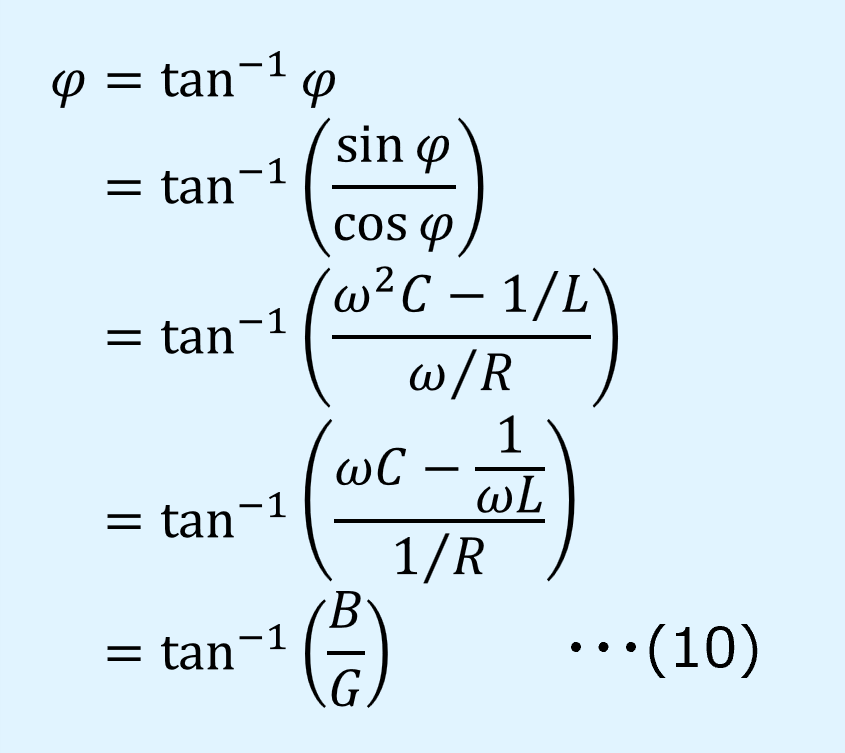
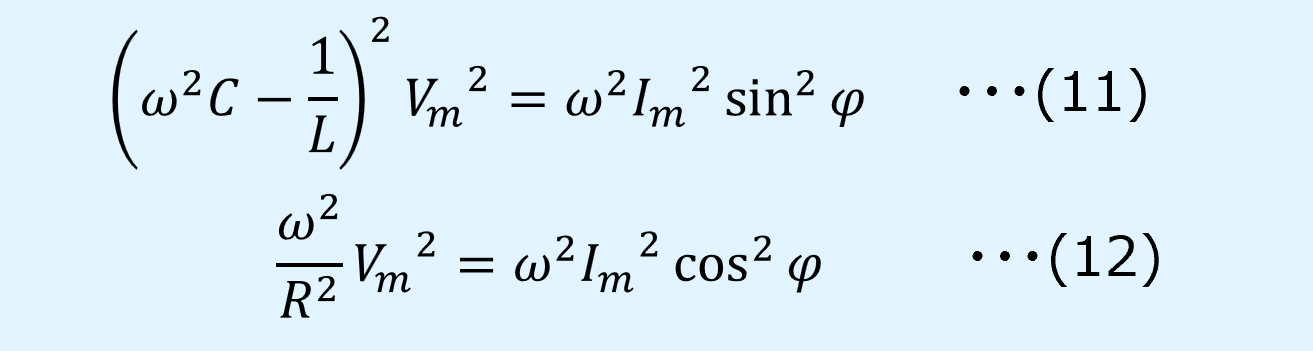
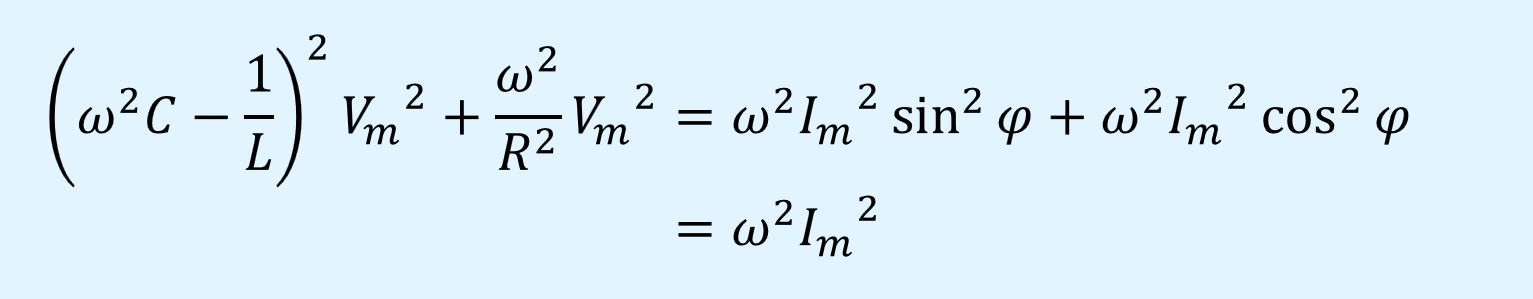
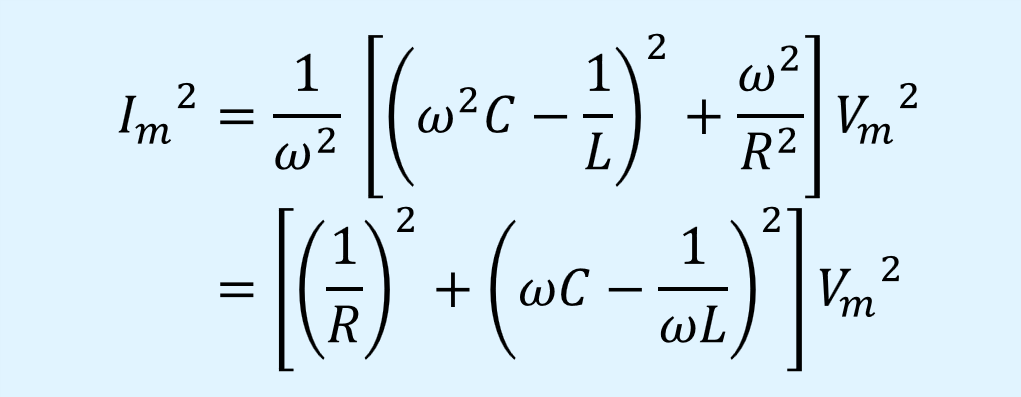
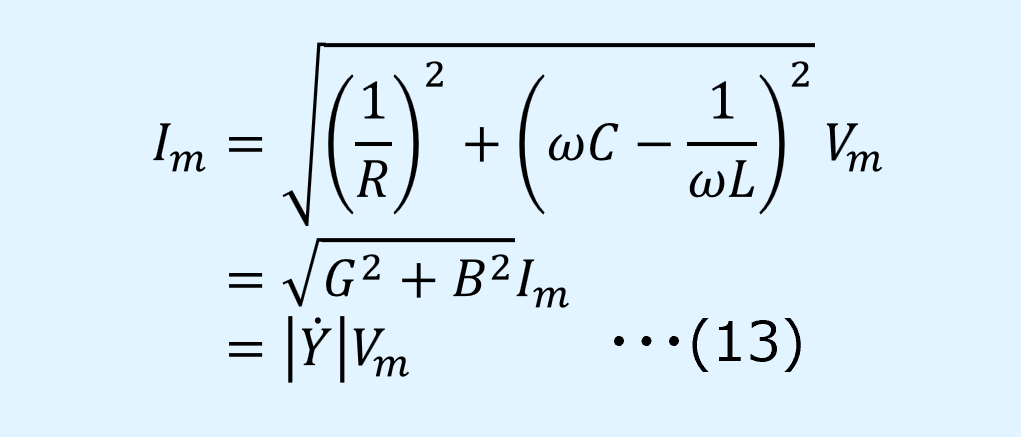
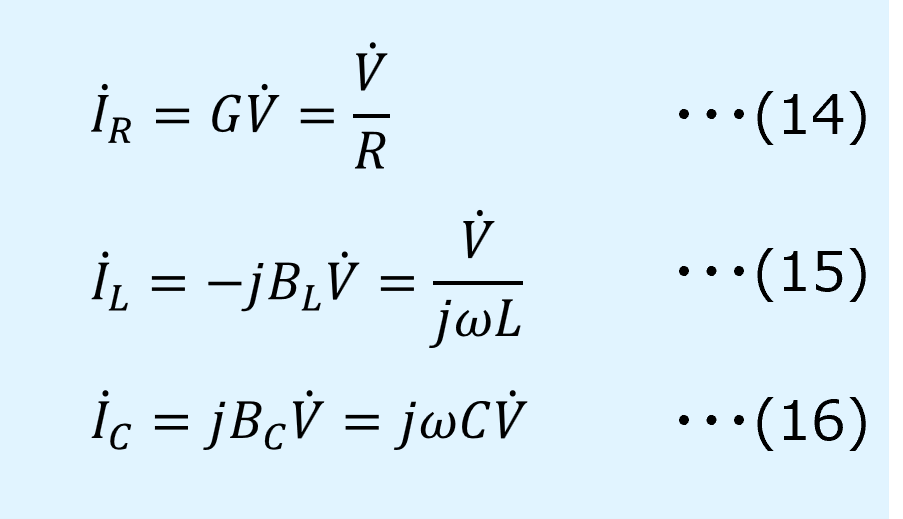
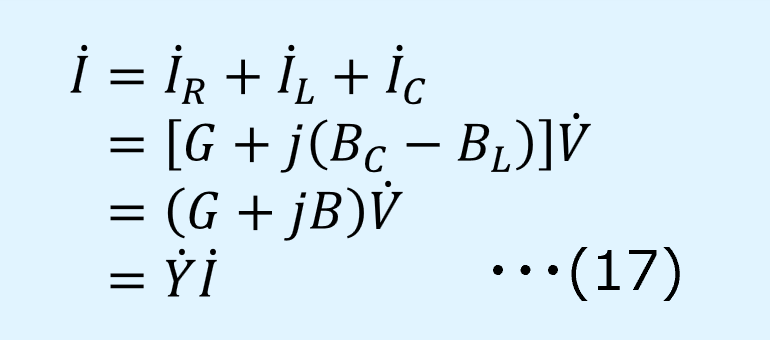
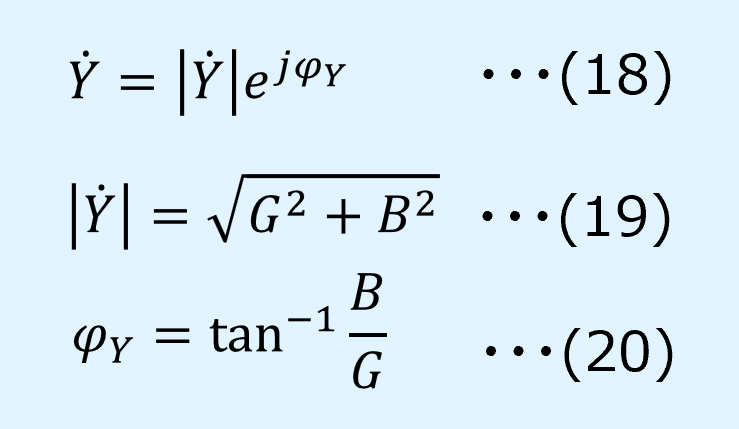
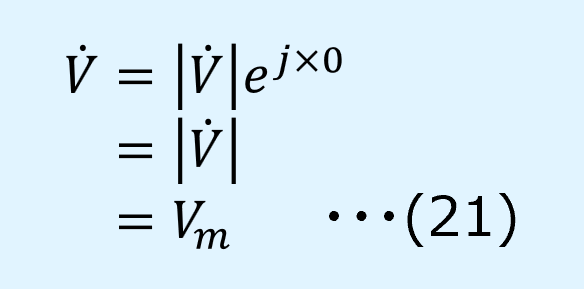
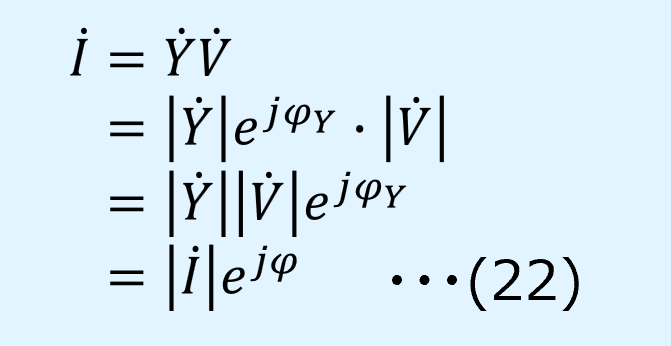
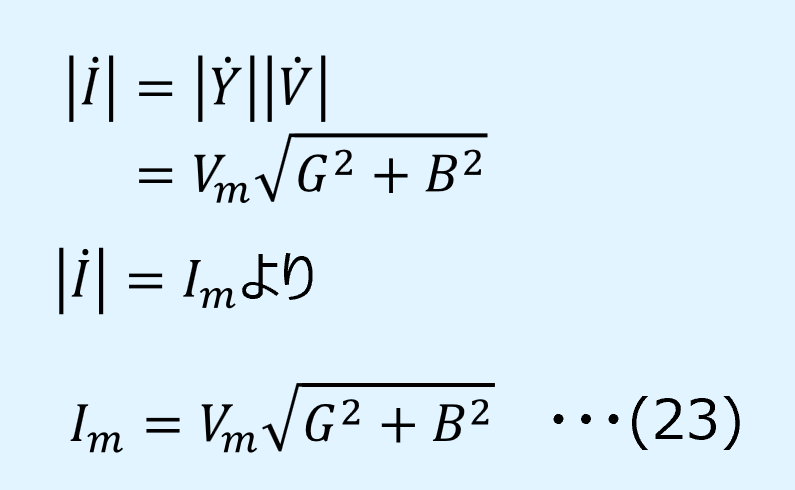
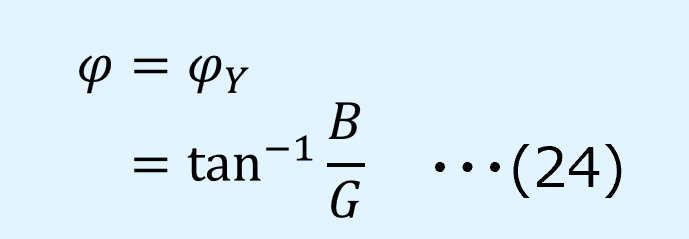
コメント