この記事では電気回路の一種であるキャパシタンス回路に交流を加える場合について説明をします。
電圧と電流の位相関係がどうなるのかについて主に扱います。
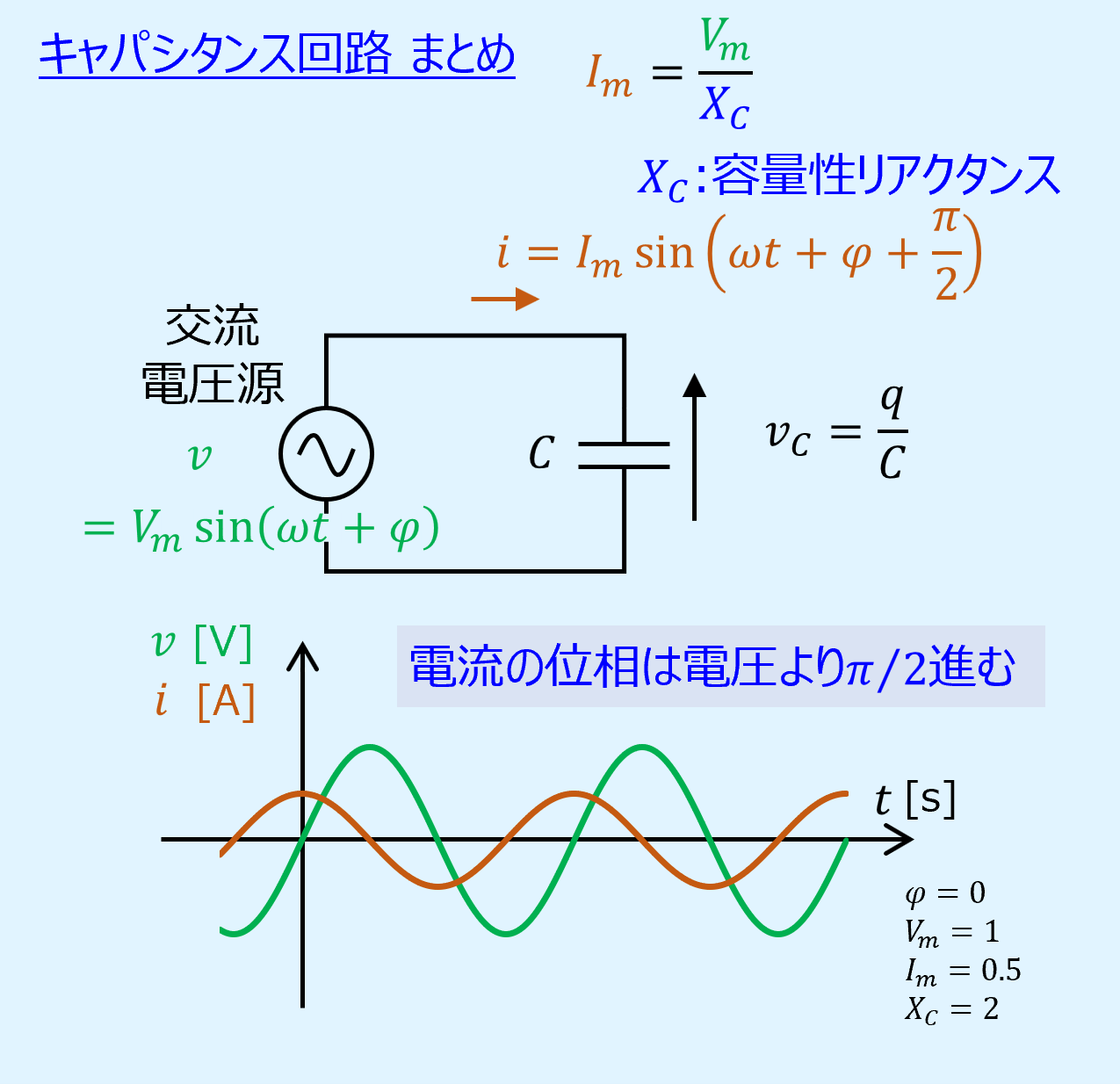
【まとめ】キャパシタンス回路
キャパシタンス回路における交流電圧と電流の関係
交流回路では電圧と電流の位相が一致するとは限りません。
キャパシタンス回路に交流電圧を加えたときに電流がどうなるのかをここでは説明します。
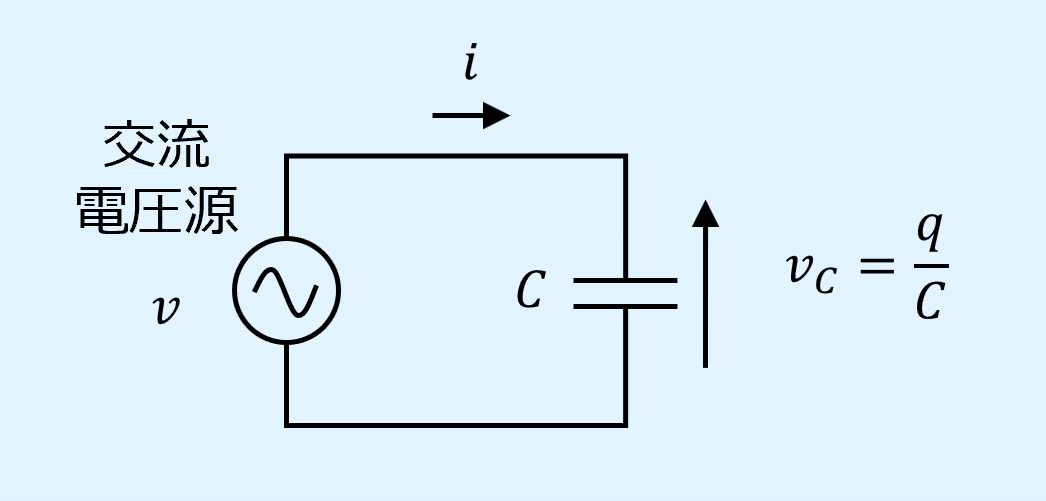
以下に交流電圧源にキャパシタンス(コンデンサ)を接続しただけの簡単なキャパシタンス回路を示します。
電源の電圧\(v\)[V]を次式で表します。
ここで、\(V_m\)は最大振幅[V]、\(\omega\)は角周波数[rad/s]、\(t\)は時間[s]、\(\varphi\)は位相[rad]を表しています。
キャパシタンス\(C\)[F]に交流電圧\(v\)が加えられるとき、キャパシタンスに蓄えられる電荷\(q\)[F]は次式で表されます。
電流\(i\)は電荷\(q\)の時間変化であるため、\(q\)を時間\(t\)で微分することで求められます。
上式を見ると、電流の位相は電圧に対し、\(+\varphi/2\)だけずれていることが分かります。
すなわち、キャパシタンスに交流電圧を加えたとき、キャパシタンスに流れる電流の位相は加えた電圧の位相より\(\varphi/2\)進むということです。
容量性リアクタンス
電流の最大振幅は次式で表されます。
式中の\(X_C\)を容量性リアクタンス(capacitive reactance)と呼びます。
容量性リアクタンスは交流電流が流れることを妨げる抵抗の一種であると考えることができます。
容量性リアクタンスと周波数は反比例の関係にあり、周波数が高くなるほど容量性リアクタンスは小さくなり、電流が流れやすくなります。
キャパシタンス回路のフェーザ表示
上記のキャパシタンス回路をフェーザ表示で計算した場合を次に示します。
電圧の複素表示とフェーザは以下の通りとなります。
次にキャパシタンスのフェーザ表示ですが、こちらは容量性リアクタンス\(X_C\)に複素数の\(-j\)を掛けたものとなります。
電圧のフェーザ\(\dot{V}\)とリアクタンスのフェーザ\(\dot{X}\)から、電流のフェーザ\(\dot{I}\)は以下となります。
上記は直交座標表示で計算した場合ですが、極座標表示で計算すると以下となります。
直交座標表示と極座標表示で計算した結果を比較すると、\(\pi/2\)の進みが\(+j\)に対応していることが分かります。
インダクタンス回路の波形とベクトル図
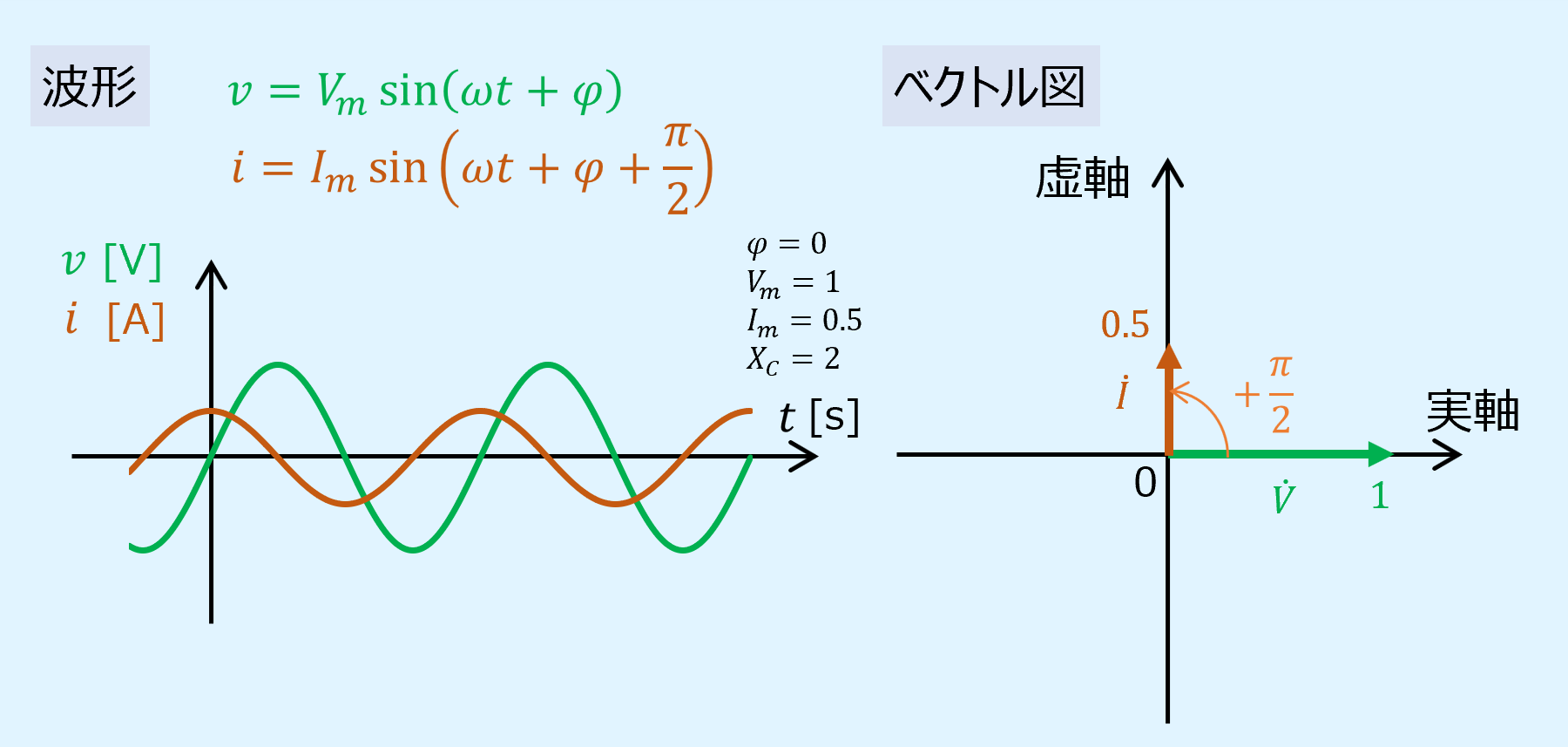
最後に波形とベクトル図がどうなるのかを示します。
以下の例は位相\(\varphi=0\)[rad]、\(V_m=1\)[V]、\(I_m=0.5\)[A]、\(X_C=2\)[Ω]の場合です。
波形の\(\pi/2\)の進みが、ベクトル図では、電圧が実軸にあるのに対し、電流は虚軸上の正方向にベクトルが引かれることで表されます。
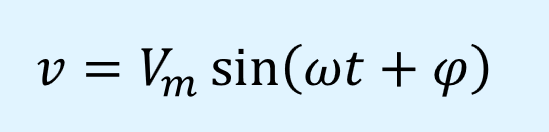
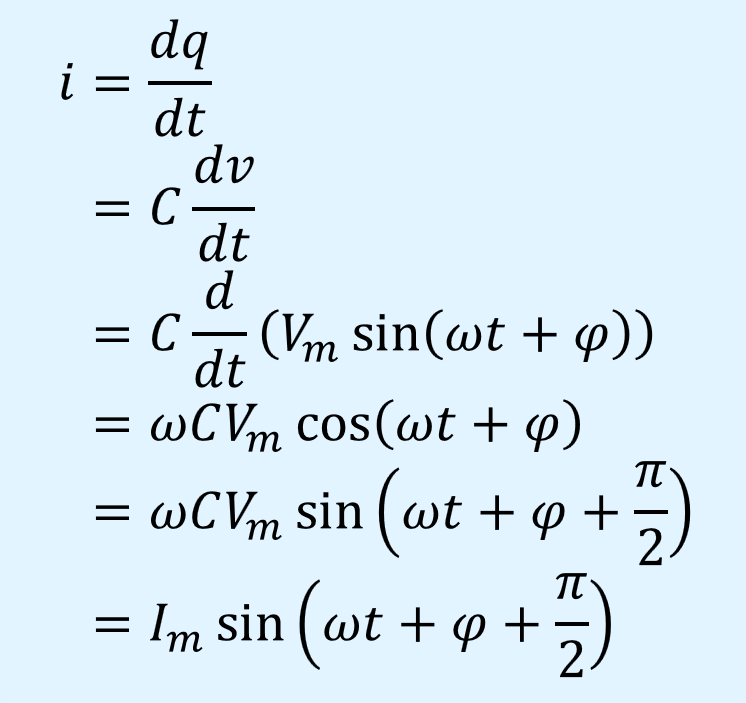
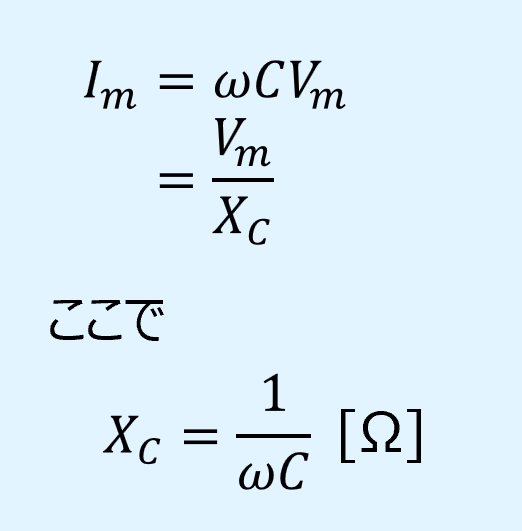
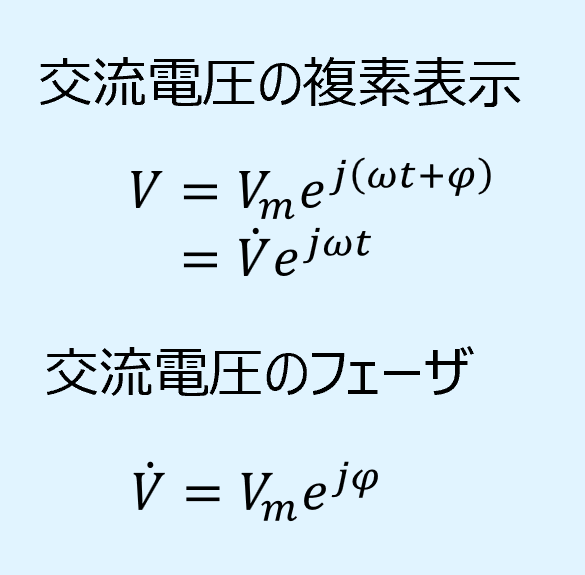
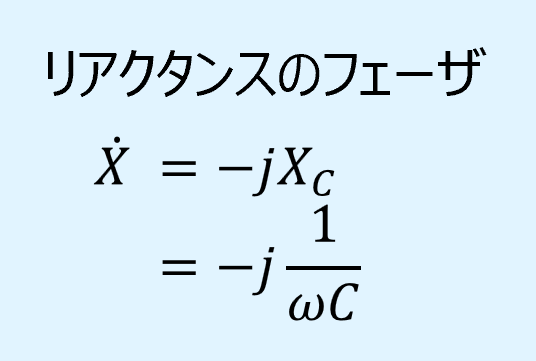
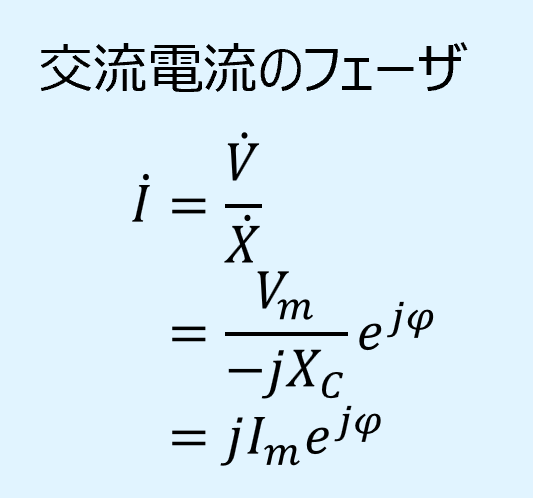
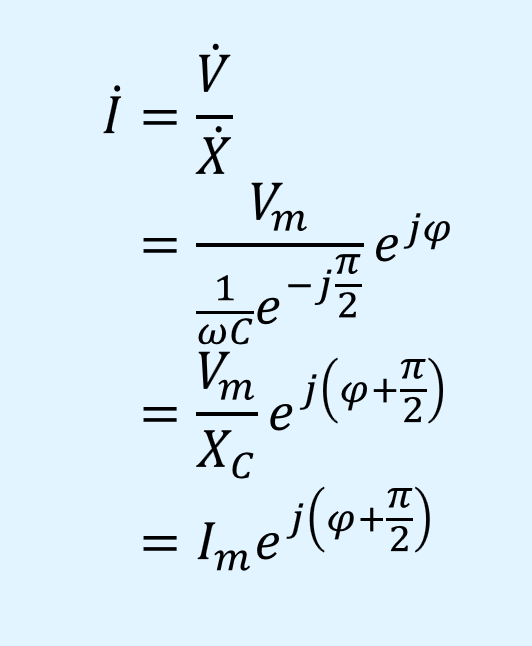

コメント