この記事では電気回路の実効値ついて説明をします。
実効値とは何なのかから、なぜ用いるのかまでを取り扱います。
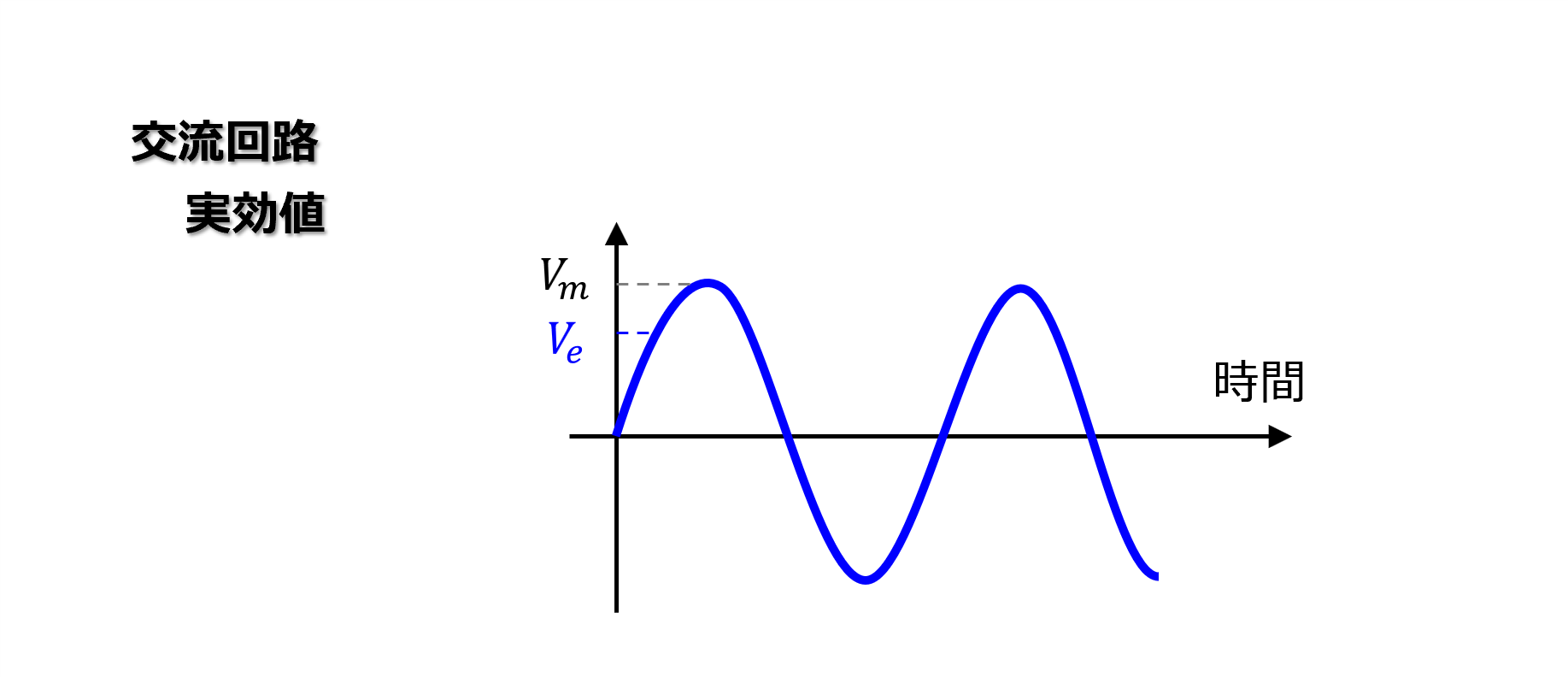
【まとめ】実効値
実効値とは
交流電圧、電流の大きさを表すのには実効値(effective value, root mean square : RMS)が用いられます。
交流と同じ電力を発生する直流電圧、電流を想定し置き換えるという考え方です。
次に実効値の計算方法を説明します。
交流の電力は、直流と同様に、電圧と電流の積で求まります。
交流電圧と電流は時々刻々と変化する瞬時値であるため、電力も瞬時値となります。
ここで、電圧と電流が加えられる負荷が抵抗\(R\)であるとすると、電力の瞬時値はオームの法則により次式となります。
このままですと、電力が時々刻々と変化してしまうため、平均値をとることにします。
交流電力の平均値\(P\)は、電力の瞬時値\(p\)を1周期分積分し、周期\(T\)で平均を取ることで求められます。
この平均電力と等しい電力を発生する直流電圧、電流が実効値\(V_e\)、\(I_e\)であるため、以下の式で定義されます。
この式は交流であればどの波形にも適用できます。
実効値\(V_e\)、\(I_e\)を用いて平均電力を表すと以下の通りとなります。
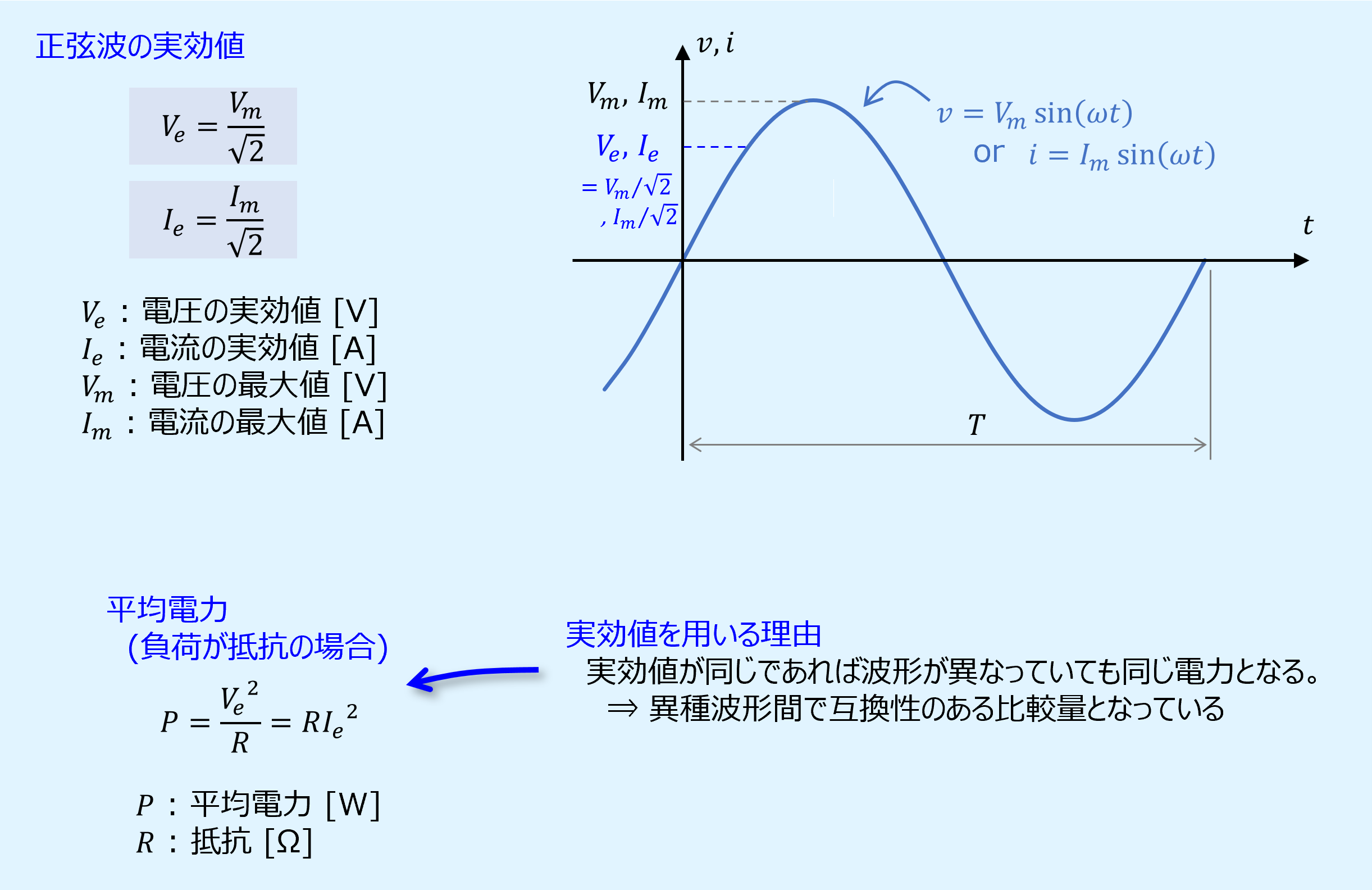
正弦波の実効値
正弦波の実効値が頻繁に用いられますので、以下に掲載します。
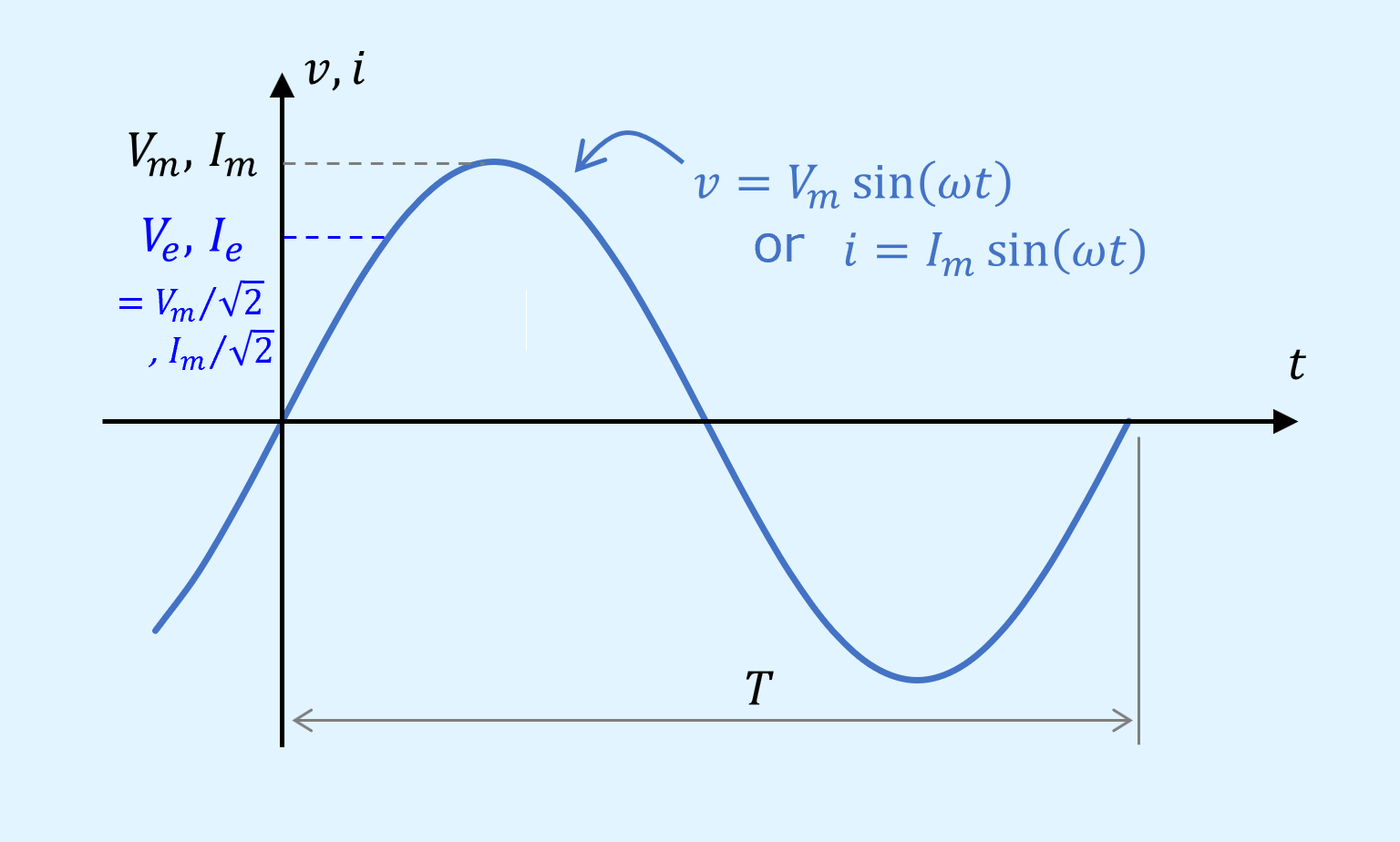
正弦波の最大値と実効値の関係をグラフで表すと以下の通りとなります。
正弦波の実効値導出仮定は以下の通りとなります。
なぜ実効値を用いるのか
電圧、電流の実効値を用いると、異なる波形間で電力に関して互換を取ることができます。
交流の電気回路で、単一の正弦波だけが流れているのなら、最大値\(V_m\)、\(I_m\)を用いるだけで済みます。
しかし、交流の電気回路は必ずしも単一の正弦波だけを流している訳ではありません。
周波数が異なる複数の正弦波から成る波形だと不都合が生じます。
例として、矩形波の場合を考えます。
最大値が正弦波と同じで\(V_m\)、\(I_m\)とすると、実効値は\(V_e=V_m\)、\(I_e=V_m\)となります。
この時負荷抵抗に加わる電力は\(P=V_m^2/R=RI_m^2\)となり、これは正弦波の電力\(P=V_m^2/2R=RI_m^2/2\)と異なります。
つまり、最大値を用いると、値が同じでも電力が異なるという事態が生じるため、比較に用いるパラメータとして不適であるということです。
これに対して実効値であれば、どの波形でも\(P=V_e^2/R=RI_e^2\)となり、比較に用いることができます。


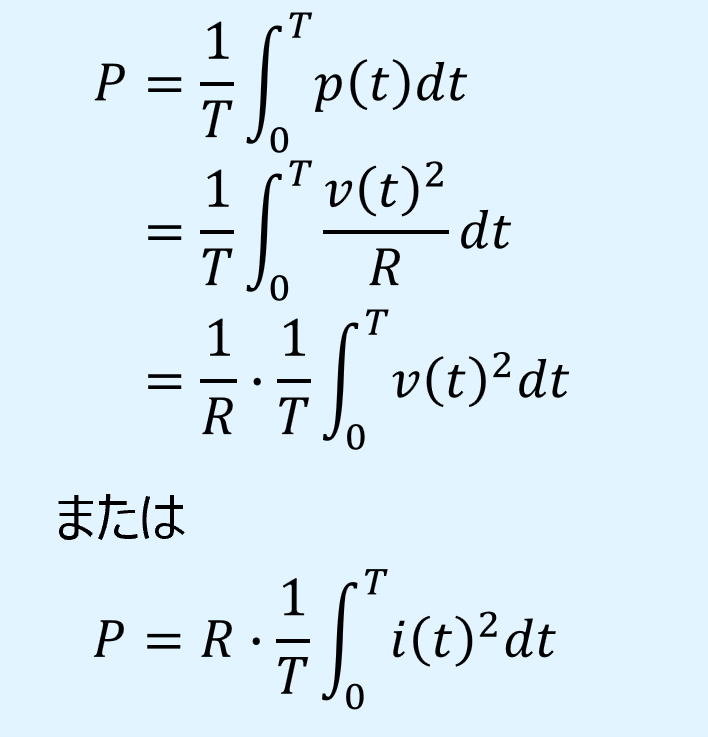





コメント