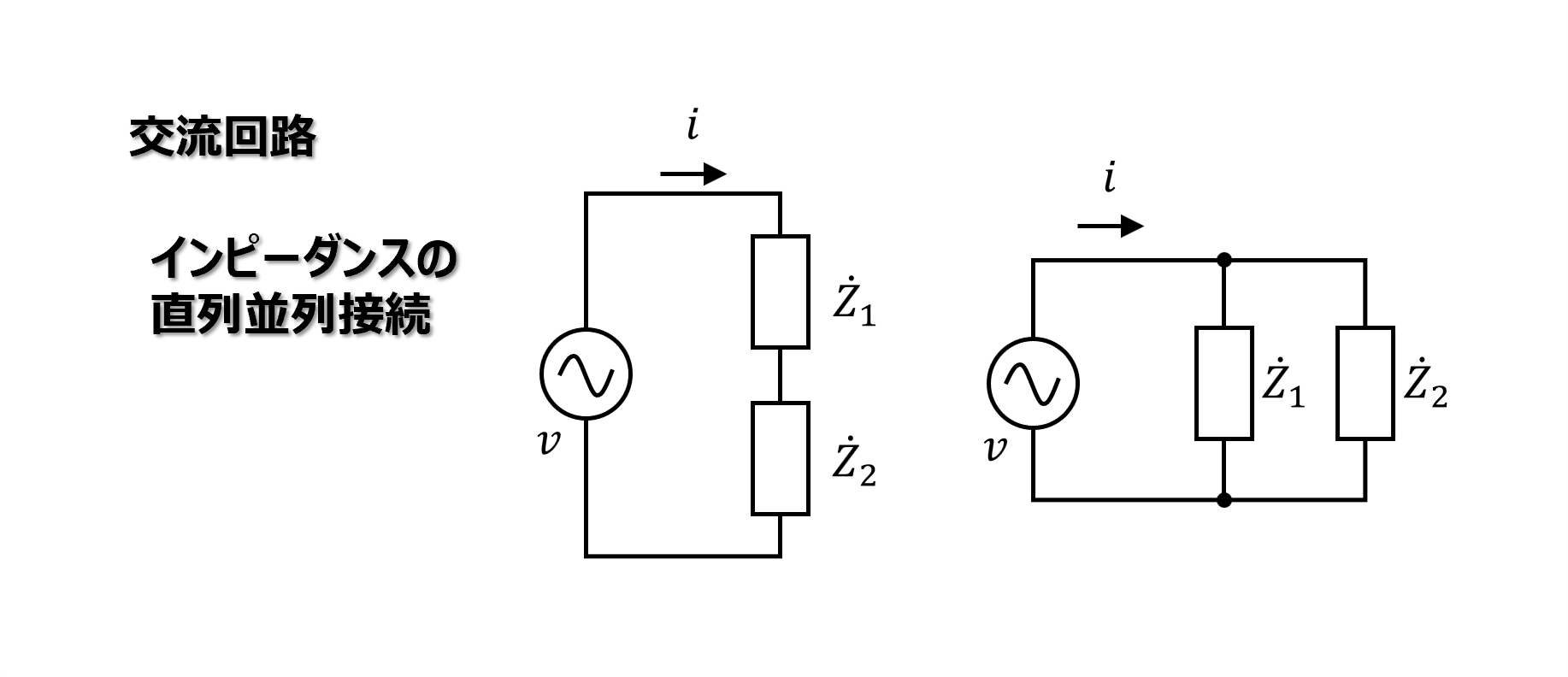
この記事では電気回路におけるインピーダンスの直列接続と並列接続について説明をします。
直列接続と並列接続における合成インピーダンスの計算方法と、並列接続の場合アドミタンスに置き換えて計算した方がよいことを述べます。
目次
【まとめ】インピーダンスの直列並列接続
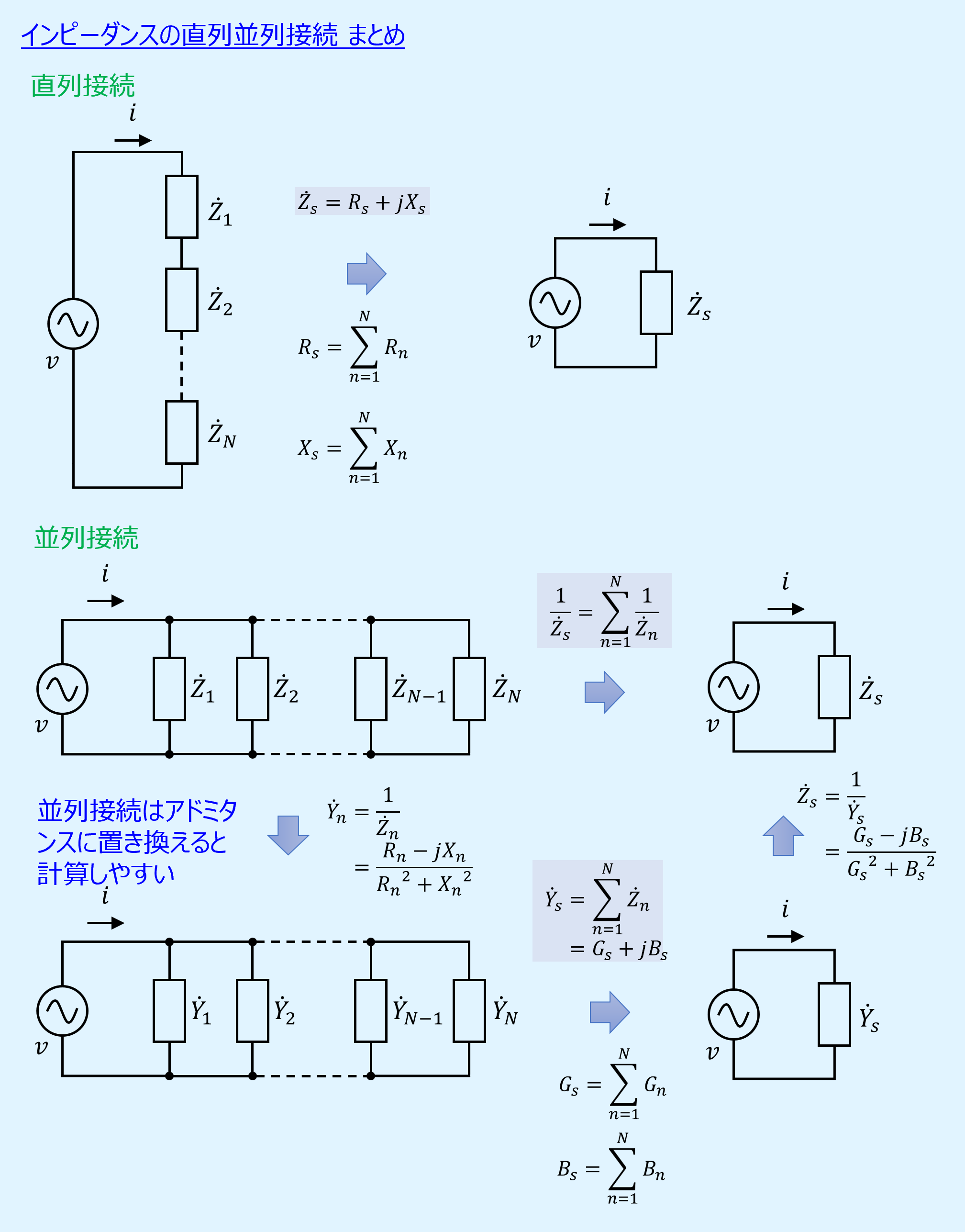
最初にまとめです。
インピーダンスの直列接続(2個)
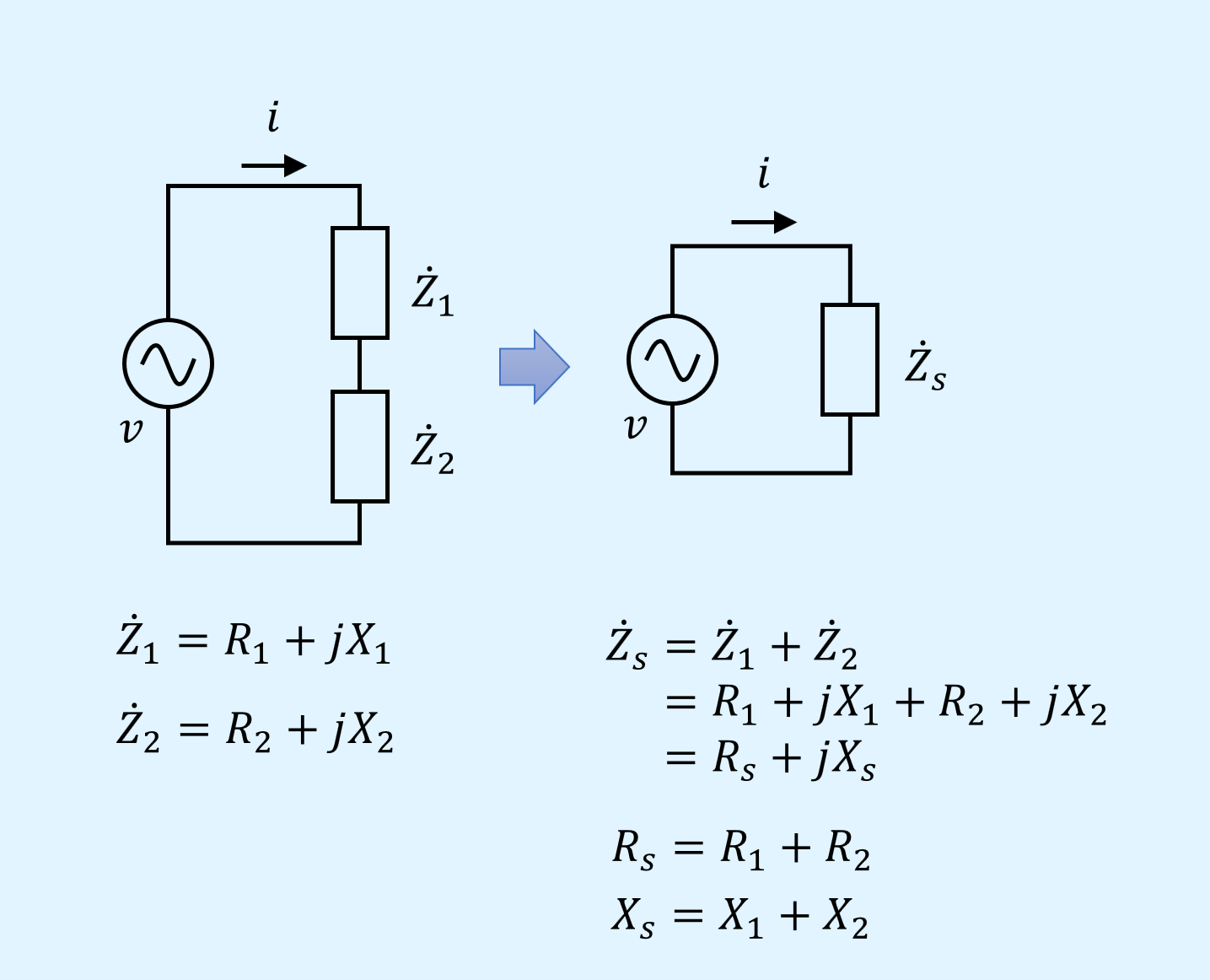
最初にインピーダンス\(\dot{Z}\)を2個直列に接続した場合を示します。
抵抗を直列接続した場合と同様に、抵抗成分を足し合わせます。
リアクタンス成分も抵抗と同様に足し合わせることで求まります。
インピーダンスの直列接続(N個)
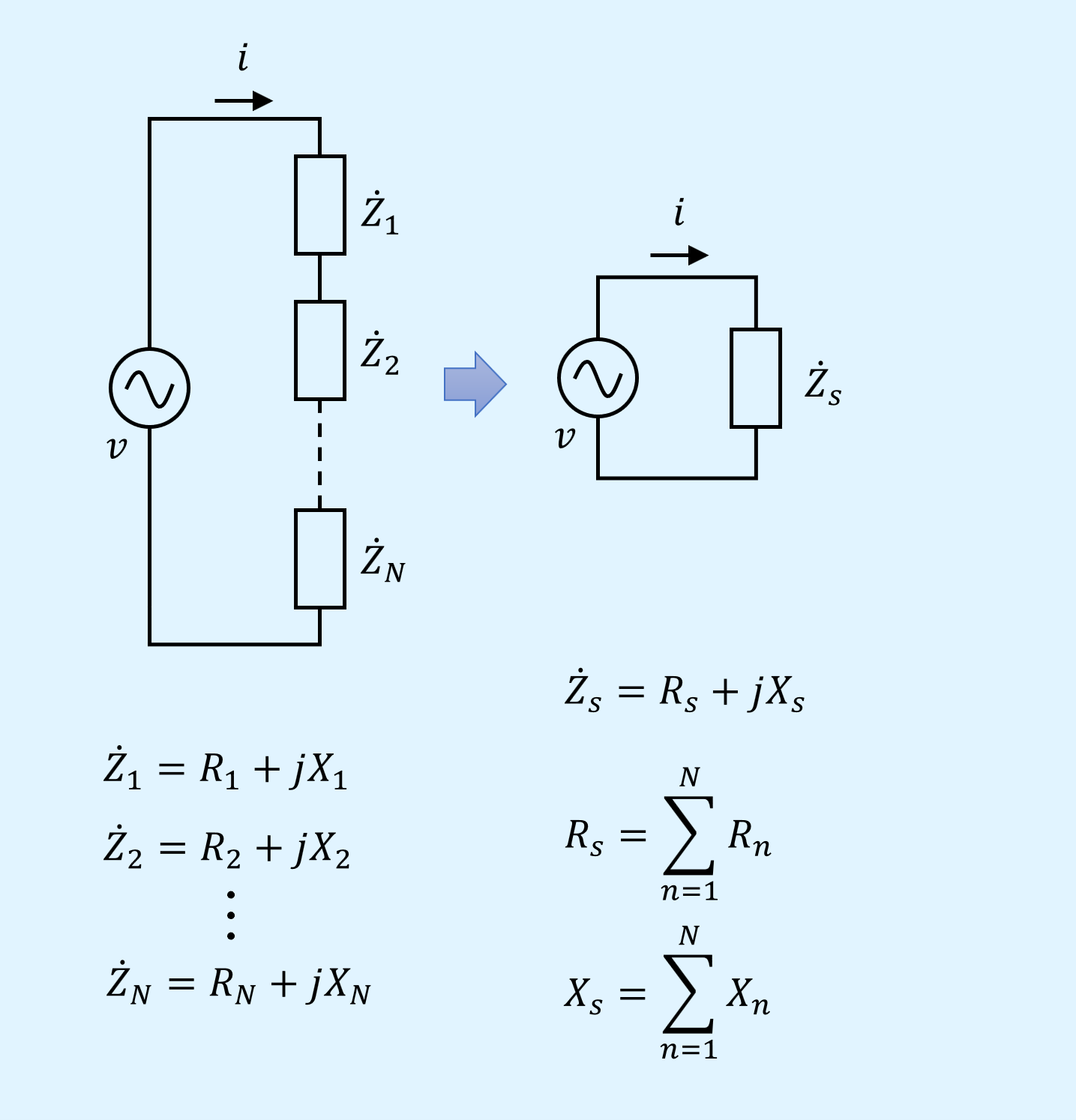
N個直列に接続した場合に拡張すると、以下となります。
すなわち、直列接続の合成インピーダンスは、抵抗成分の総和を実数部、リアクタンス成分の総和を虚数としたものとなります。
インピーダンスの並列接続(2個)
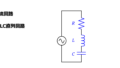
次に並列接続の場合の合成インピーダンスを求めます。
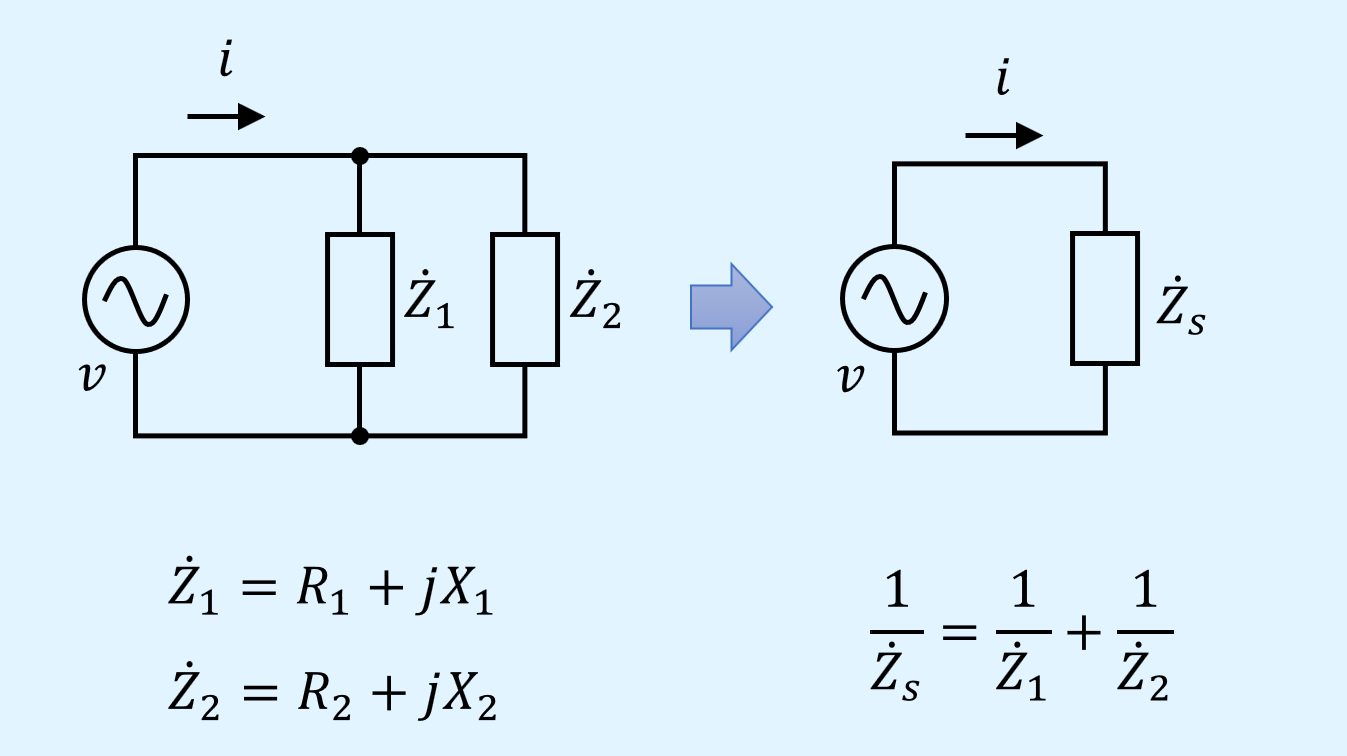
2個並列に接続した場合を以下に示します。
抵抗を並列に接続した場合と同様となっており、インピーダンスの逆数\(1/\dot{Z}_1\)、\(1/\dot{Z}_2\)の和を取ったものが、合成後のインピーダンスの逆数\(1/\dot{Z}_s\)となります。
\(1/\dot{Z}_s\)を式展開すると以下となります。
ここから逆数を取り、\(\dot{Z}_s\)を求めます。
分子の実数部、虚数部を\(a_1\)、\(b_1\)、分母の実数部、虚数部を\(a_2\)、\(b_2\)とすると、\(\dot{Z}_s\)は以下となります。
代数に置き換えずに、直接\(\dot{Z}_s\)を求めると以下になりますが、かなり手間がかかります。
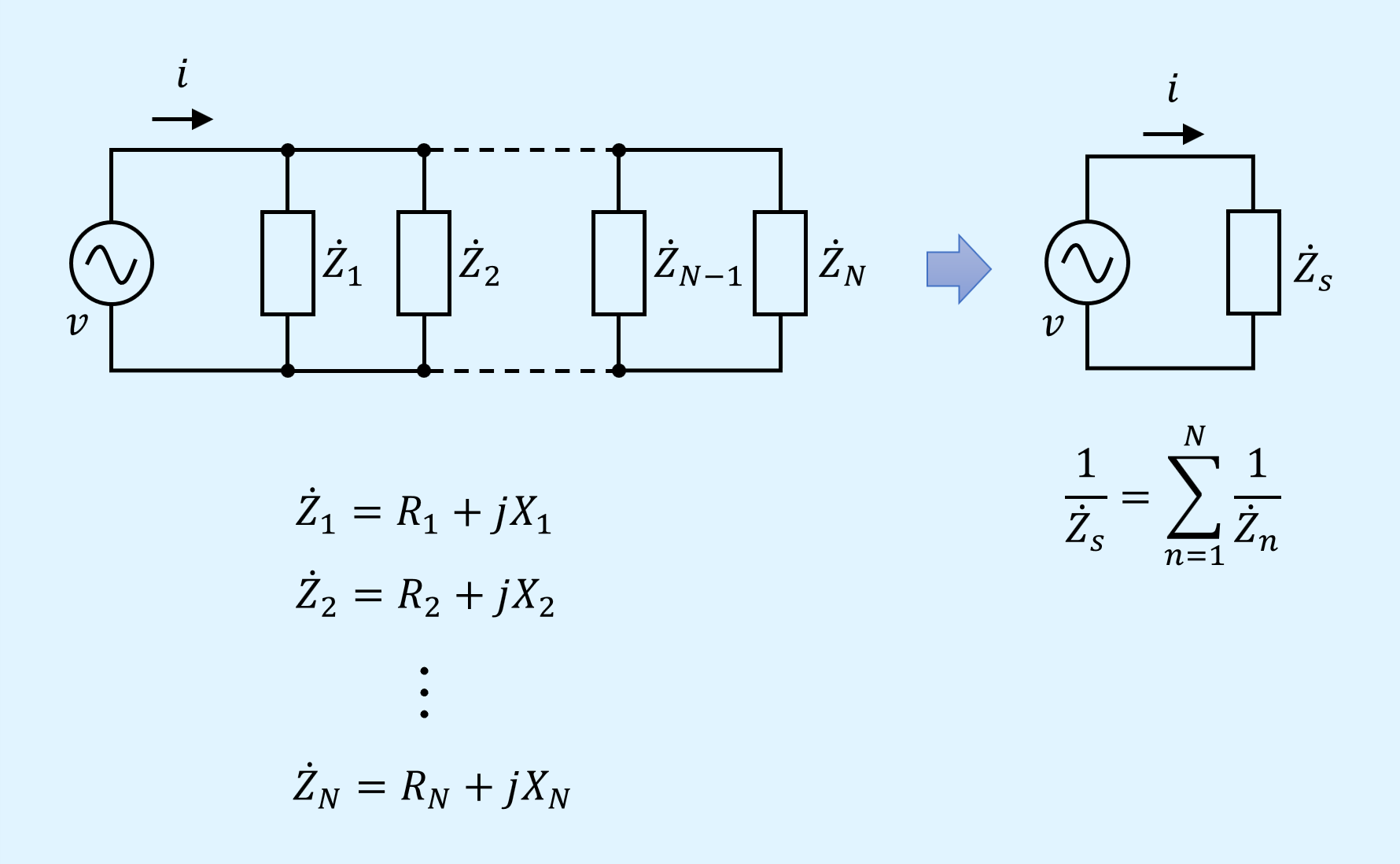
インピーダンスの並列接続(N個)
N個の並列接続に拡張した場合も同様で、各素子のインピーダンスの逆数\(1/\dot{Z}_n\)の総和を取ったものが合成後のインピーダンスの逆数\(1/\dot{Z}_s\)となります。
式で表すと簡単ですが、これを抵抗\(R\)とリアクタンス\(X\)で計算しようとすると、先に示した2個並列接続の場合のように手間がかかります。
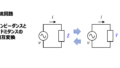
そこで、インピーダンス\(\dot{Z}\)をアドミタンス\(\dot{Y}\)に変換することで計算を容易にします。
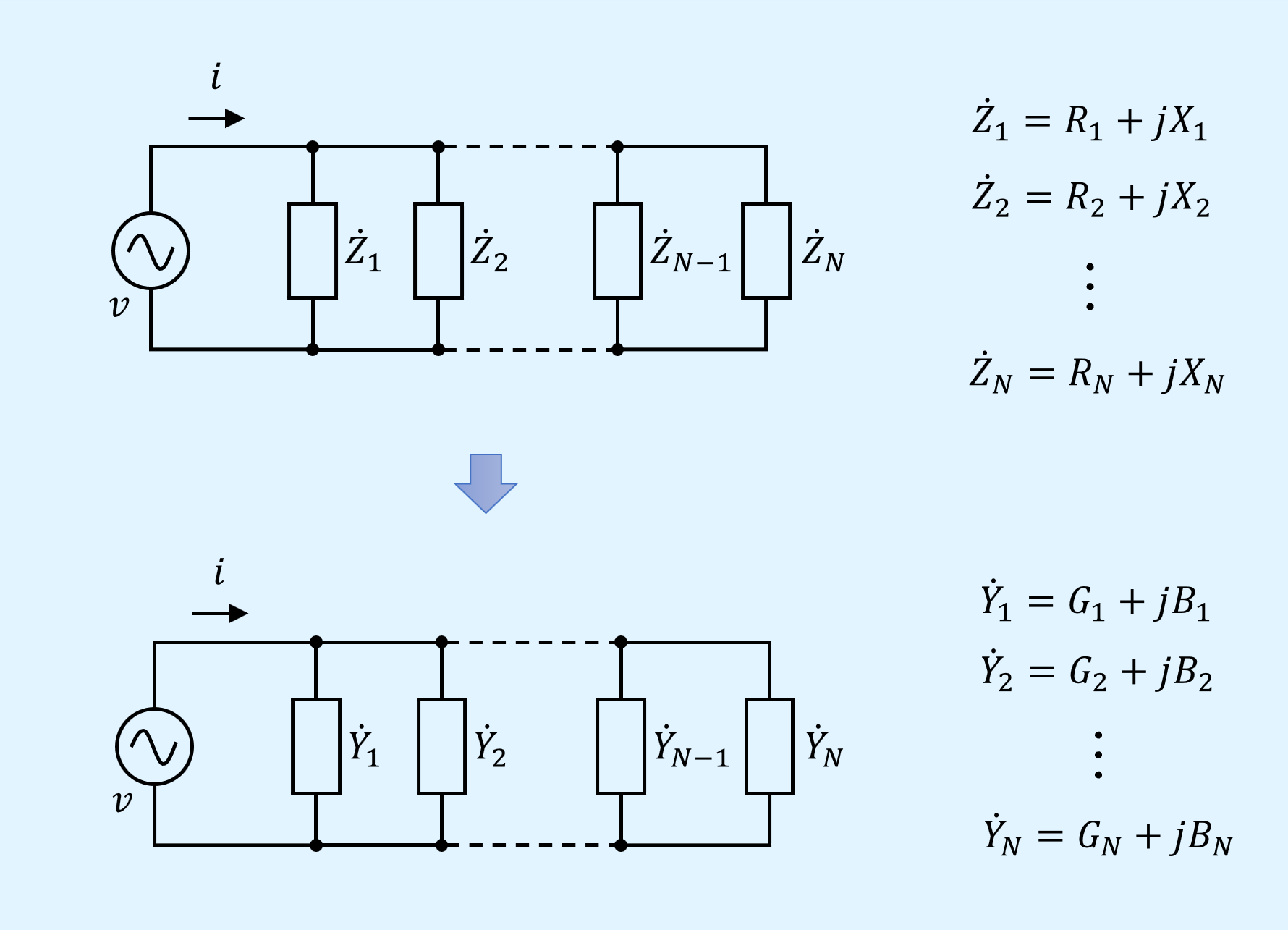
並列接続はアドミタンスへ変換して合成する
以下に示すように、それぞれのインピーダンス\(\dot{Z}_n\)をアドミタンス\(\dot{Y}_n\)に変換します。
逆数を取ることでインピーダンス\(\dot{Z}_n\)をアドミタンス\(\dot{Y}_n\)に置き換えることができます。
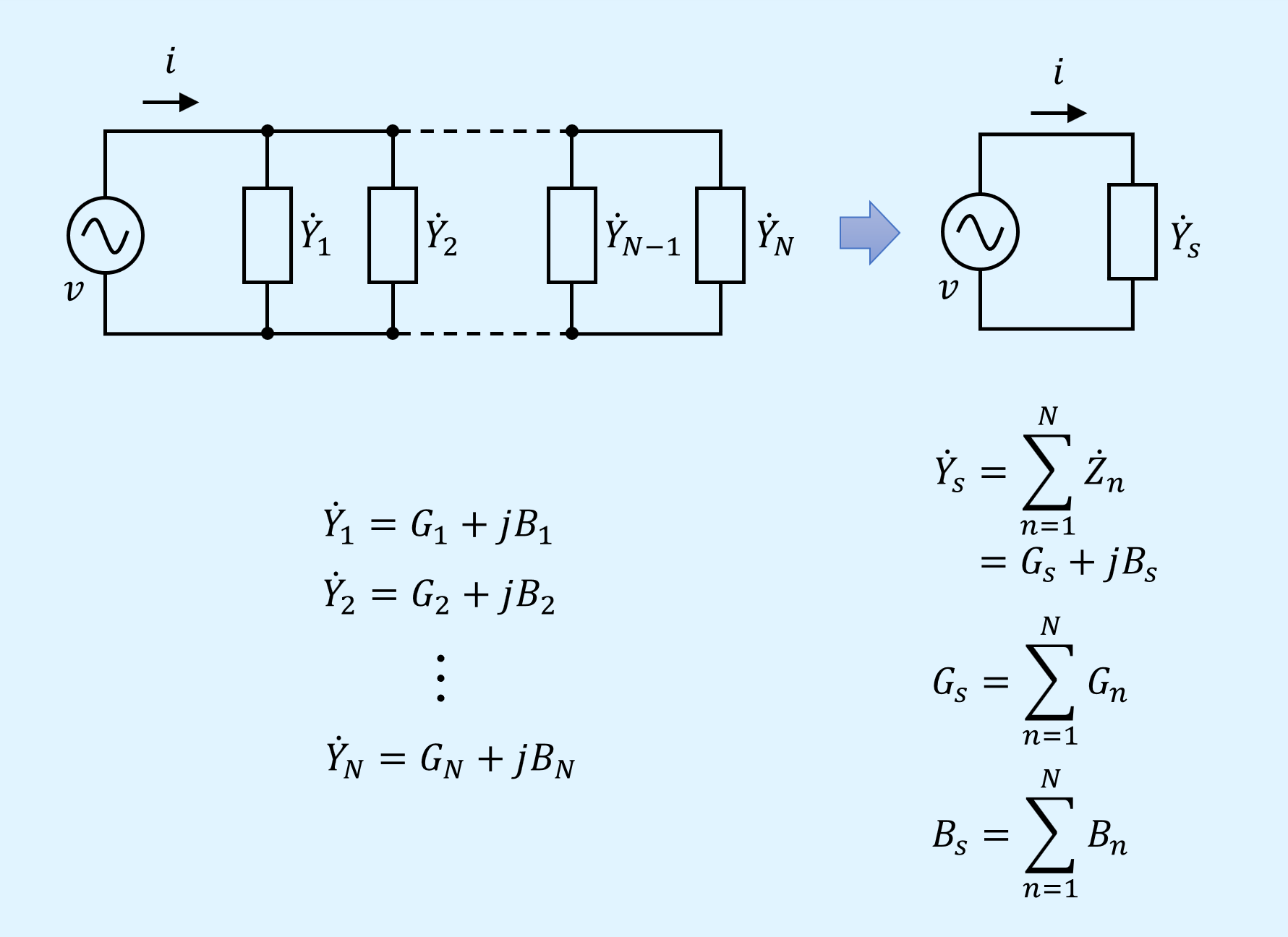
アドミタンス\(\dot{Y}_n\)を並列接続した回路の合成アドミタンス\(\dot{Y}_s\)は、コンダクタンスの並列接続と同様に、各アドミタンス\(\dot{Y}_n\)の総和となります。
合成アドミタンス\(\dot{Y}_s\)のコンダクタンス\(G_s\)とサセプタンス\(B_s\)は各素子のコンダクタンス\(G_n\)とサセプタンス\(B_n\)の総和でとなります。
そして、合成アドミタンス\(\dot{Y}_s\)の逆数を取れば、必要だった合成インピーダンス\(\dot{Z}_s\)が得られます。
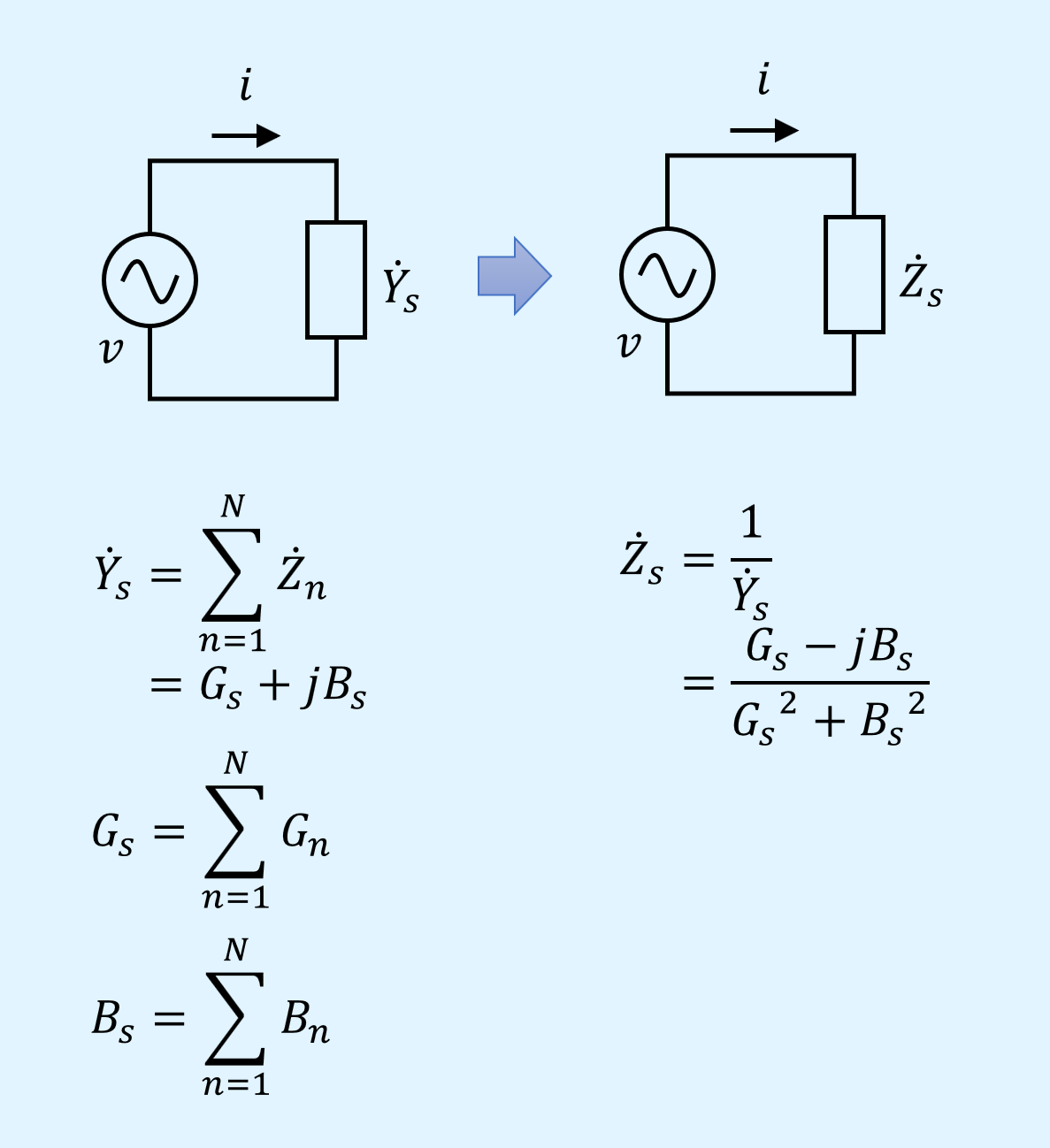
並列アドミタンスが並列インピーダンスになることの確認
最後に並列接続されたインピーダンスをアドミタンスに変換しても、結果が同じになることを確認します。
合成インピーダンス\(\dot{Z}_s\)とその要素であるコンダクタンス\(G_s\)とサセプタンス\(B_s\)、及びコンダクタンス\(G\)、サセプタンス\(B\)、抵抗\(R\)、リアクタンス\(X\)の関係は次式で表されます。
以上より\(N=2\)の場合、
上式の分母を変形すると以下となります。
よって、合成インピーダンス\(\dot{Z}_s\)は以下のように式変形されます。
これはインピーダンスを2個並列に接続した場合の式と同じであり、アドミタンスに変換しても結果が同じになるということになります。
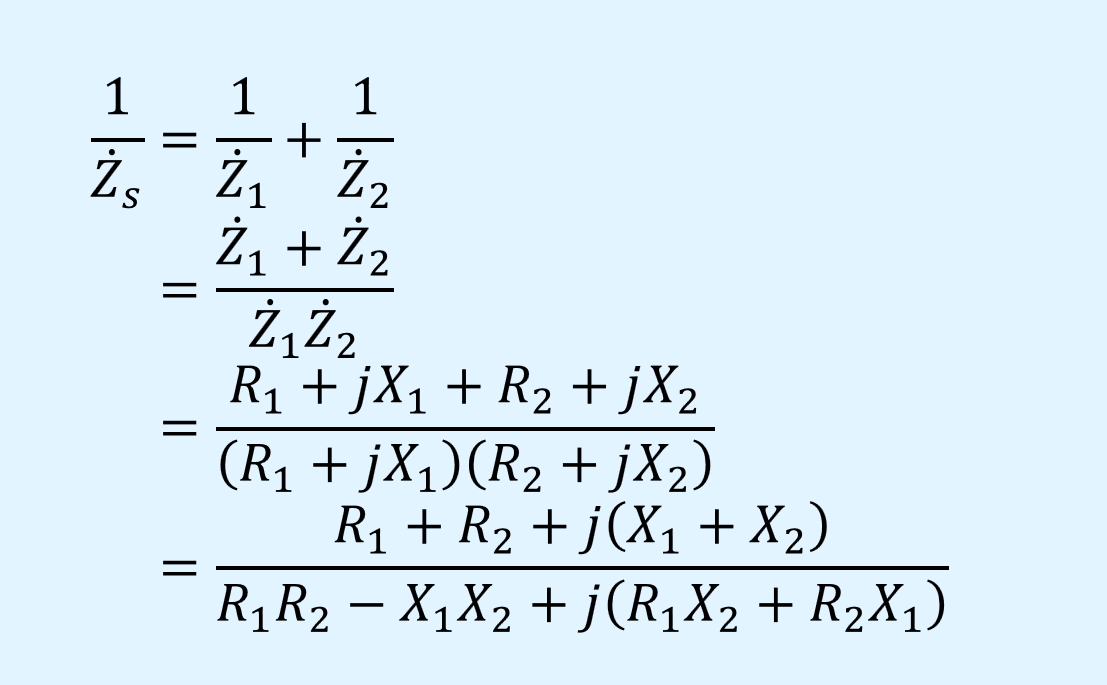
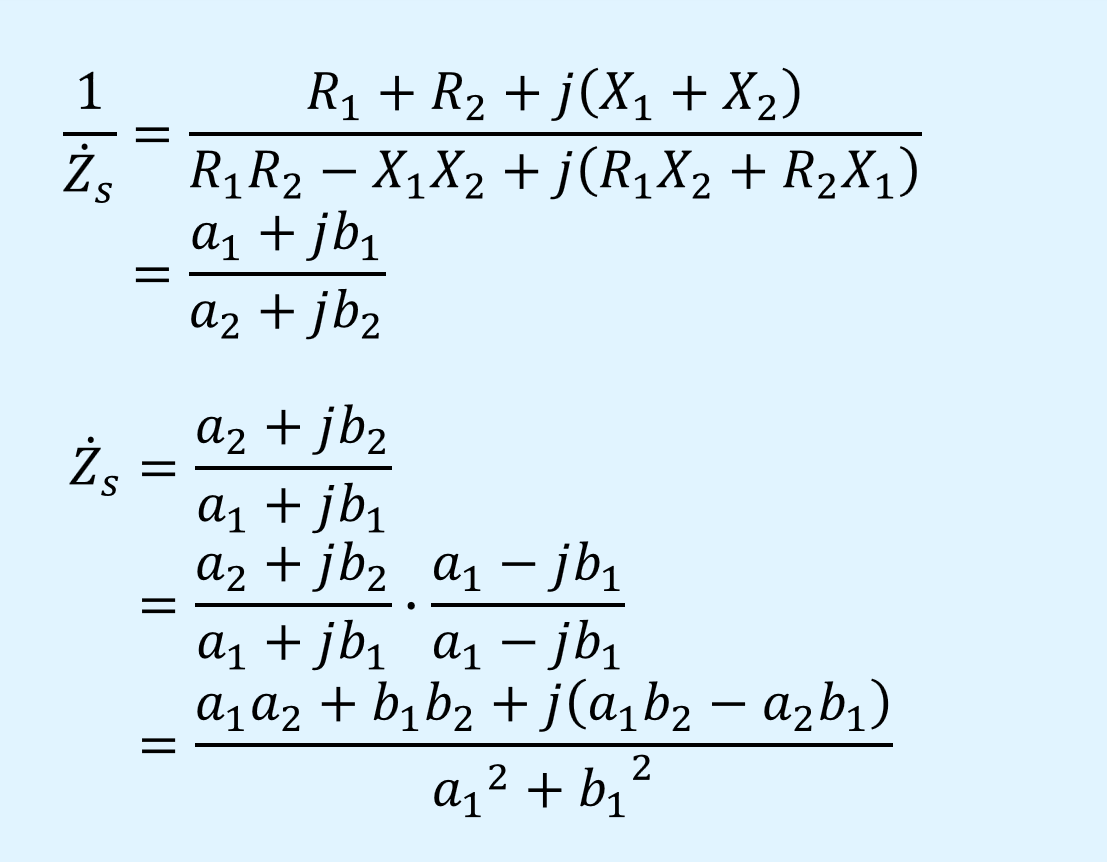
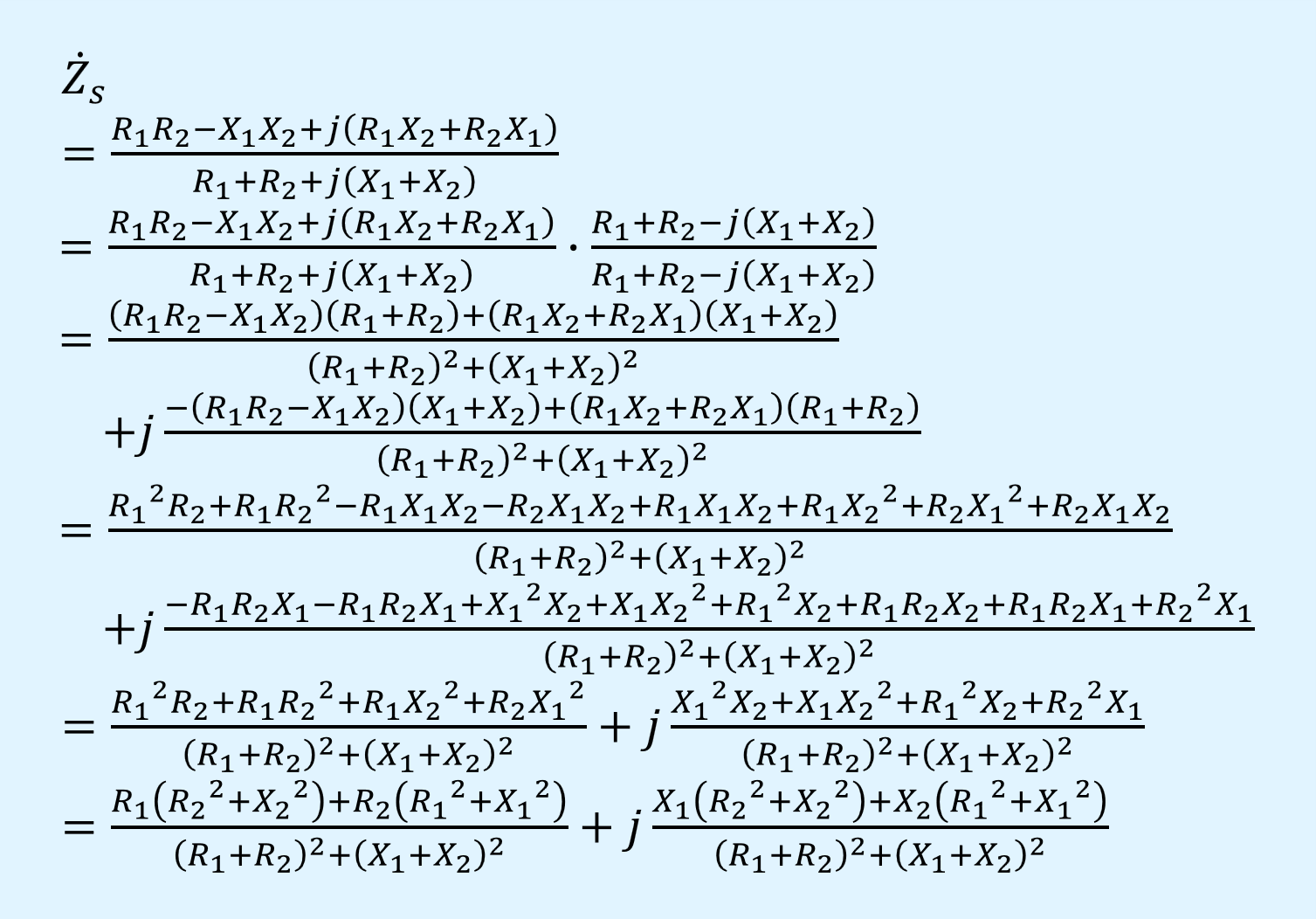
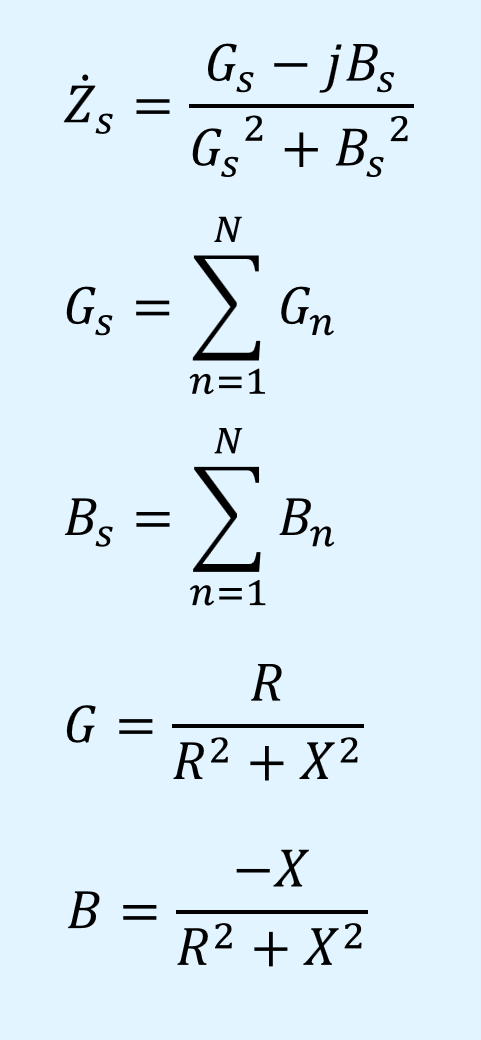
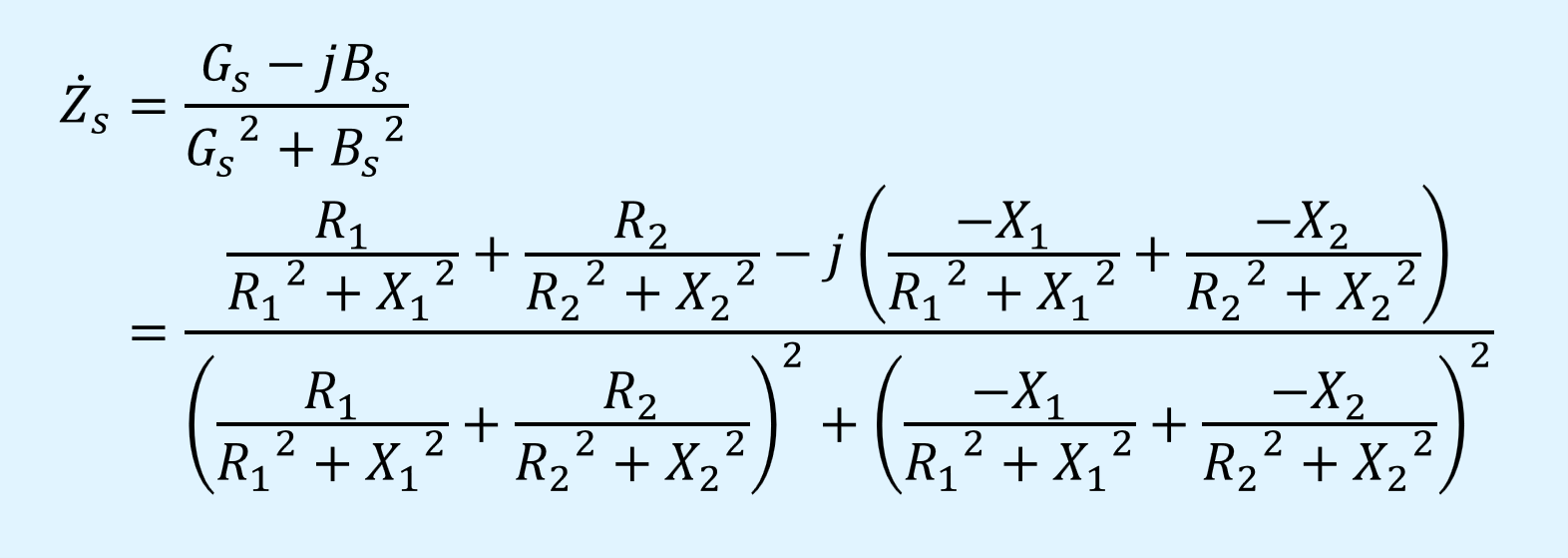
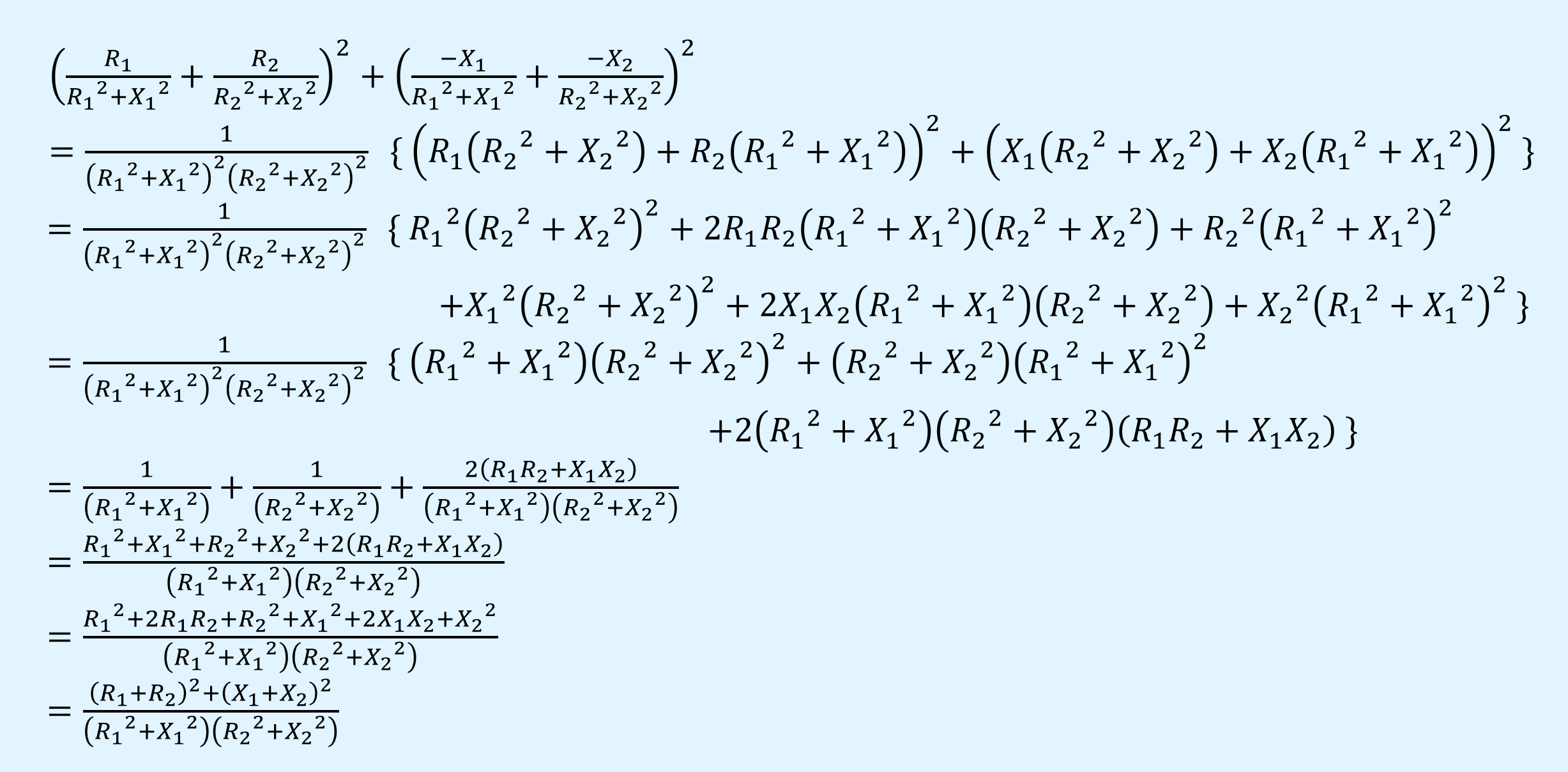
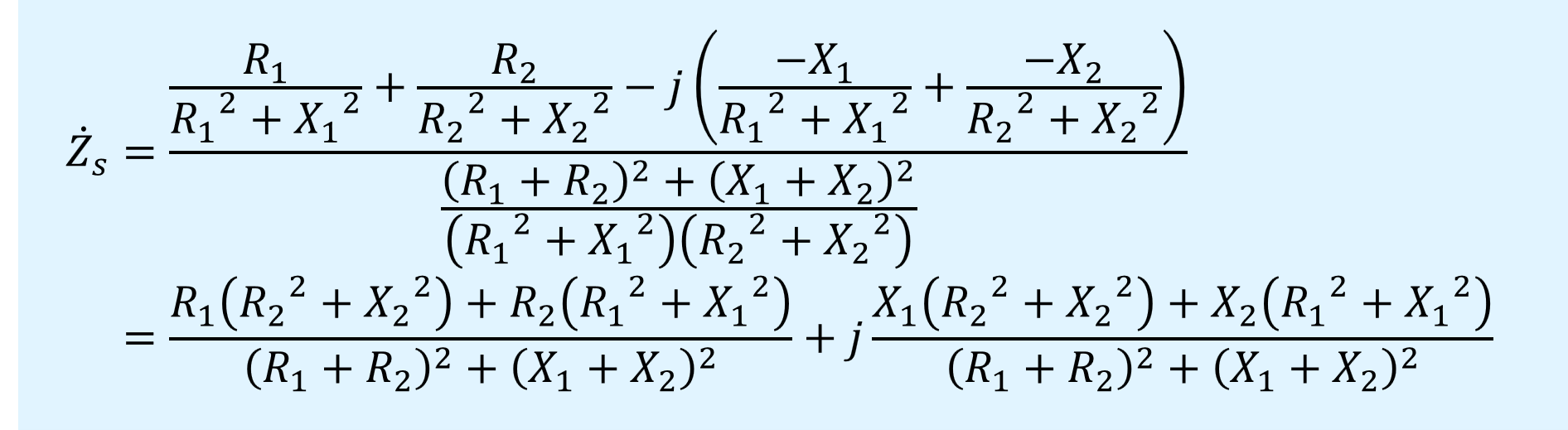
コメント