この記事では電気回路や信号処理で生じる波形の合成について説明をします。
別の記事で周波数が同じ場合について説明しましたが、ここでは周波数が異なると波形がどうなるのかを示します。
【まとめ】波形の合成 その2 (周波数が異なる場合)
最初にまとめです。
周波数が異なる波形の合成式
周波数の異なる2つの波形\(v_1\)、\(v_2\)を次のように表します。
ここで、\(\omega_1\)、\(\omega_1\)は角周波数、\(t\)は時間を表します。
最大振幅は1、位相は0としています。
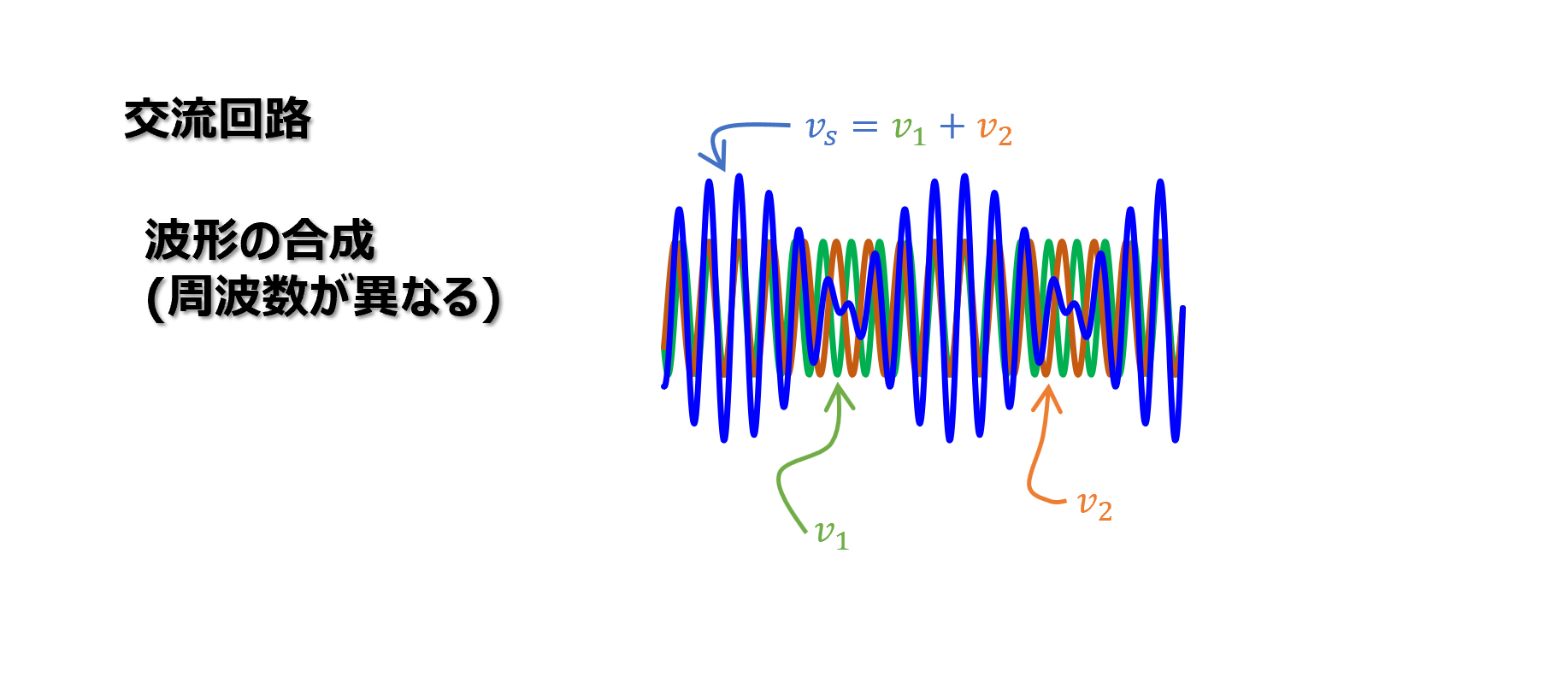
\(v_1\)、\(v_2\)を合成した波形\(v_s\)は次の通りとなります。
ここで、\(\omega_c\)は\(\omega_1\)と\(\omega_2\)の中心角周波数、\(\Delta\omega\)は\(\omega_c\)からの\(\omega_1\)、\(\omega_2\)の周波数差で、次の式で表されます。
また、式導出の仮定は以下の通りとなります。
うなりの波形
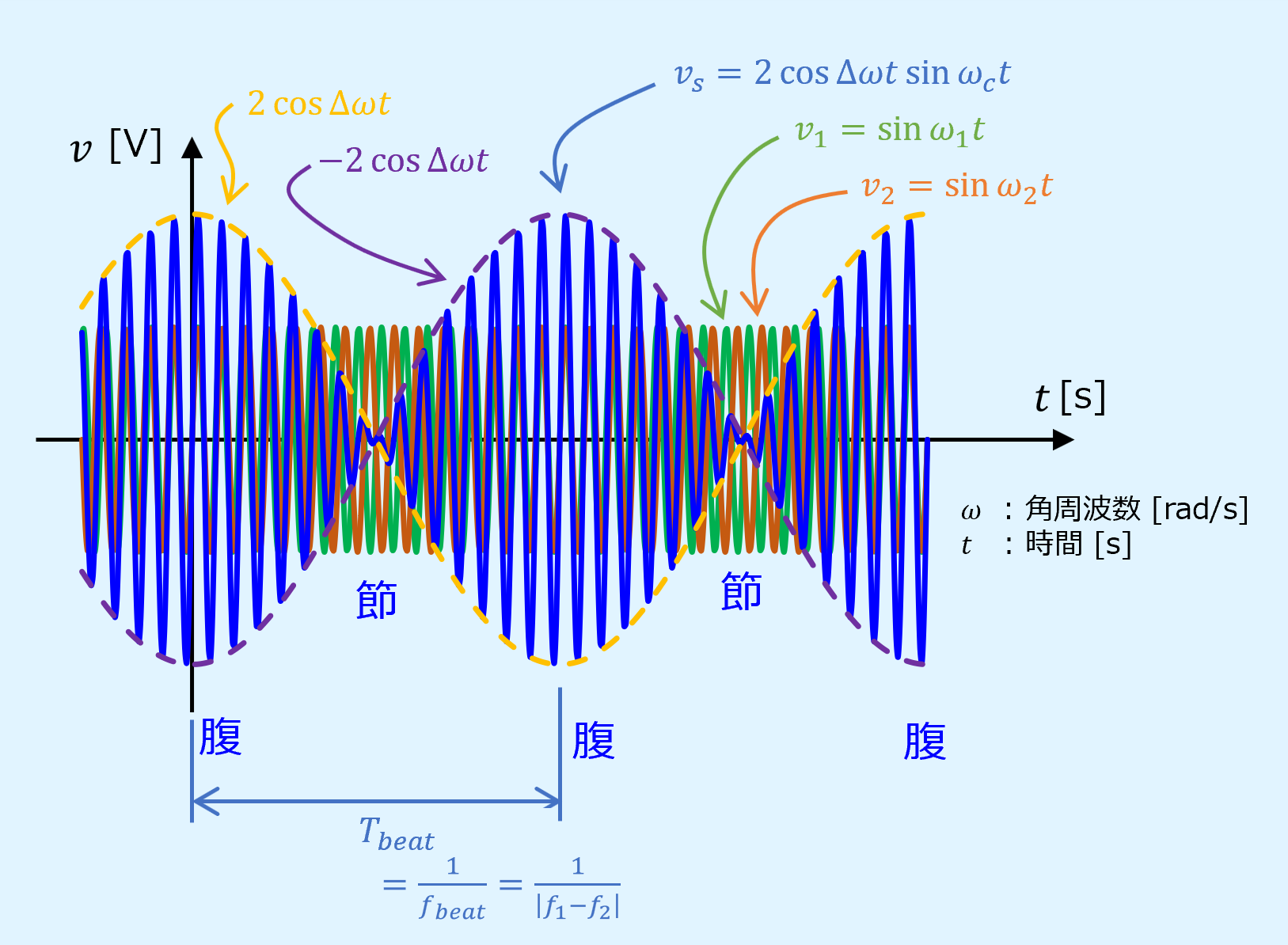
上式から、周波数の異なる2つの波形を合成すると、中心角周波数\(\omega_c\)の正弦波の振幅が\(\Delta\omega\)で周期的に変動していることになります。
この変動のことをうなり(beat)と呼びます。
うなりの波形を以下に図示します。
振幅が最大となる点を腹、最小となる点を節と呼びます。
ここで、振幅の変動角周波数が\(\Delta\omega\)であるのに対し、うなりの角周波数は倍の\(2\Delta\omega\)となっていることに注意しましょう。
よって、うなりの周波数\(f_{beat}\)は次式で表されます。
すなわち、うなりの周波数は元の2つの正弦波の周波数差となります。
2つの周波数の差が大きい程うなりの周波数は高く、差が小さい程低くなります。
なぜうなりが生じるのか、波形から理解する
周波数が異なる2つの正弦波を合成するとうなりが生じることを、数式では理解できたと思いますが、波形からも理解しておきましょう。
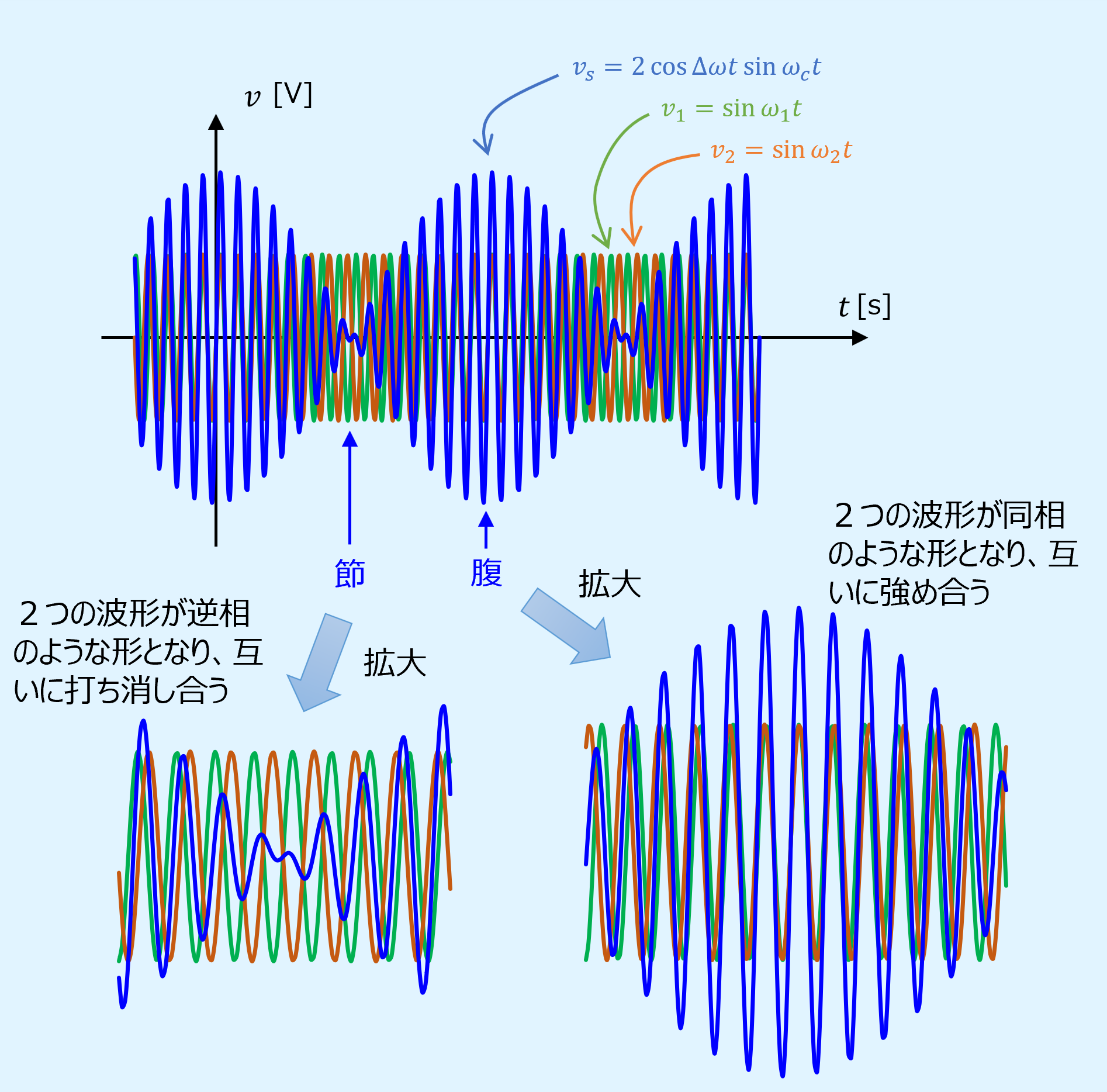
腹と節の個所を拡大した図を以下に示します。
腹の部分では2つの波形の正負が一致する同相のような形となり、互いに強め合うために振幅が大きくなります。
一方、節の個所では2つの波形の正負が逆転する逆相のような形となり、互いに打ち消し合うため振幅が小さくなります。
このように、波形の正負関係が周波数が異なるため徐々にがずれていき、強め合ったり打ち消し合ったりを繰り返してうなりを形成します。

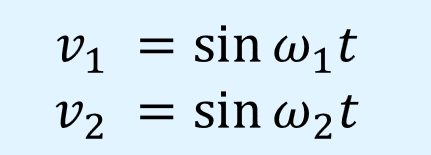
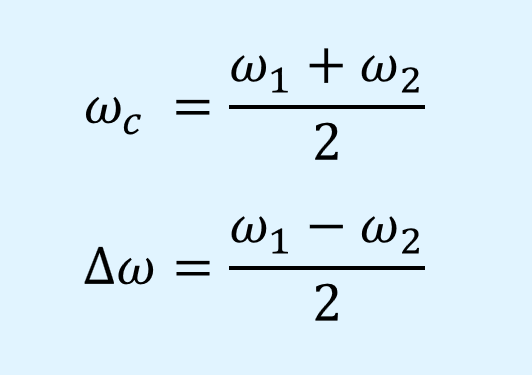
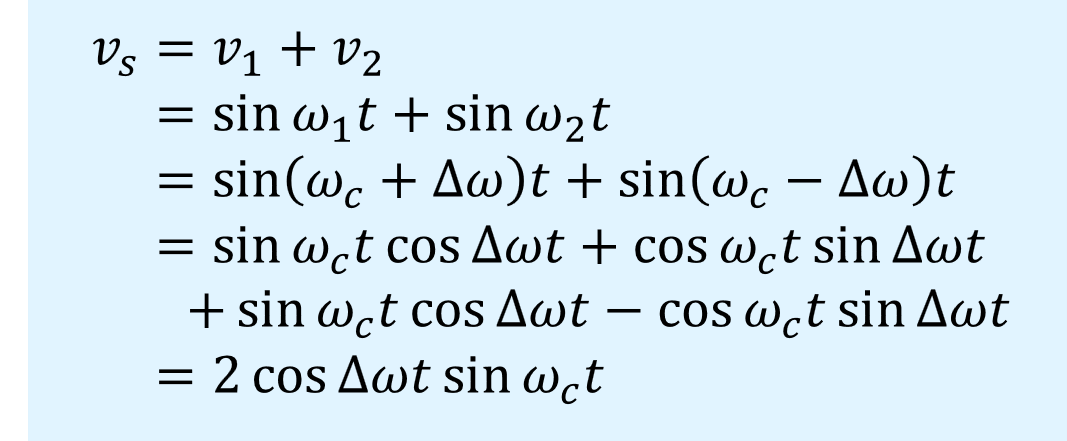
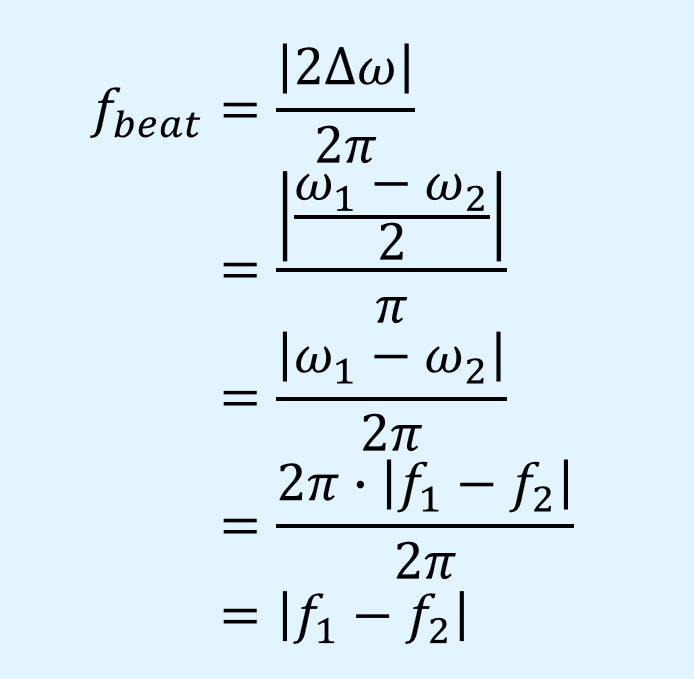

コメント