複合命題と論理演算子

最初にまとめです。

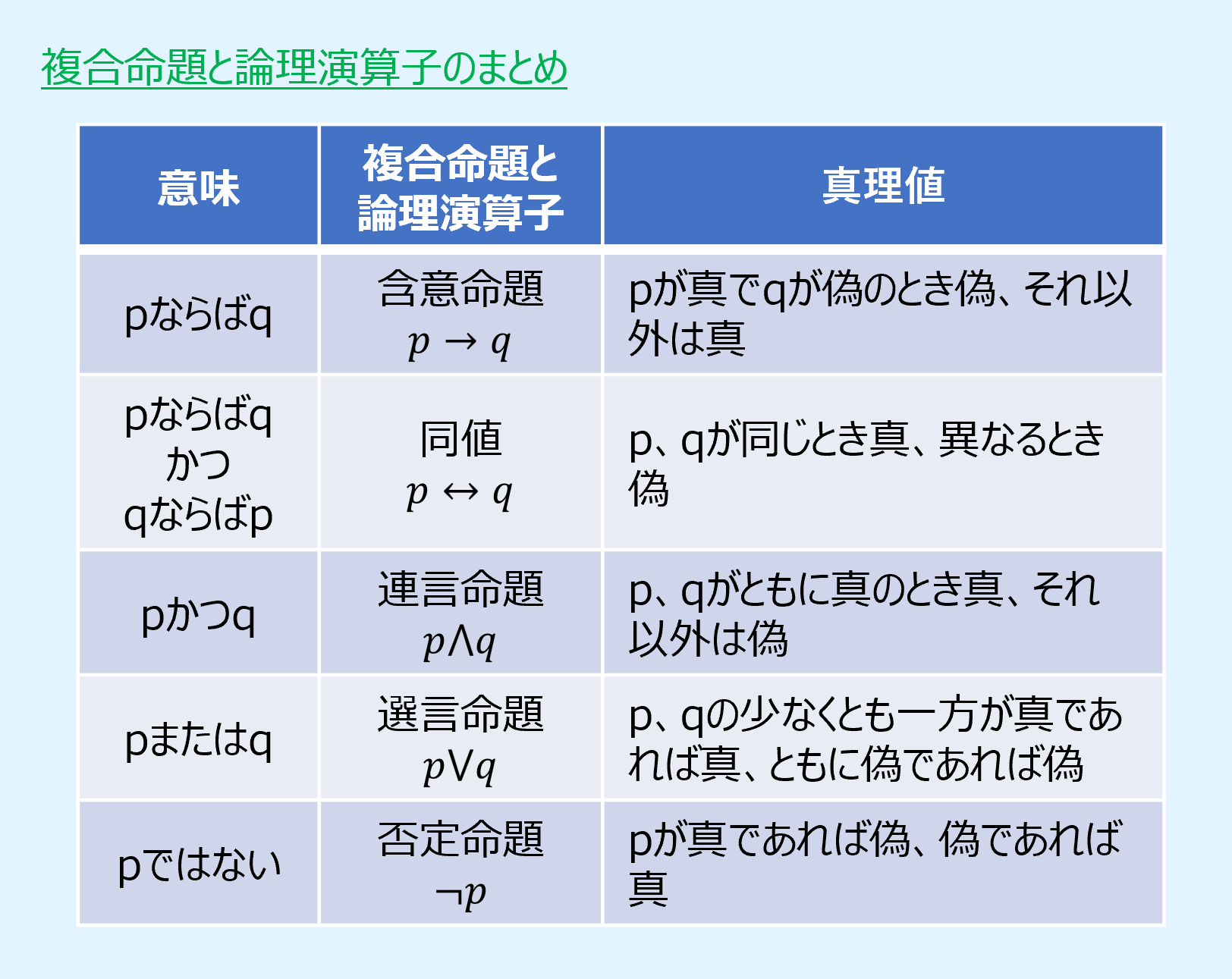
複合命題と論理演算子の一覧

複数の命題を「かつ」、「または」などで結んで作られた命題を複合命題(compound proposition)あるいは合成命題といいます。

この「かつ」、「または」を論理演算子として記号化し、複合命題を定式化したものが情報処理や論理回路でよく見る論理式となります。

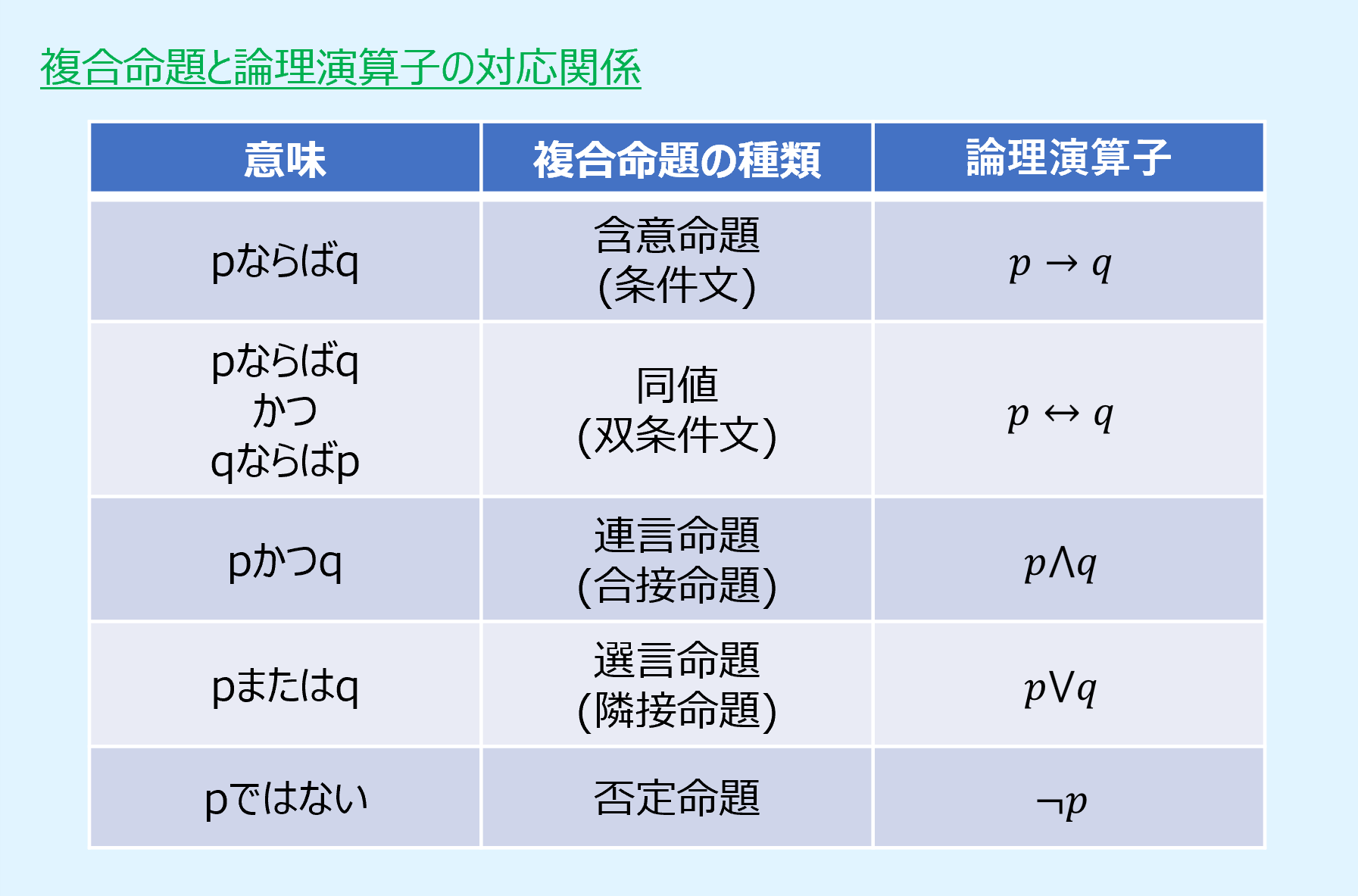
以下に複合命題とそれに対応する論理演算子を示します。

以降でそれぞれの複合命題と論理演算子について説明をします。

含意「pならばq」「p→q」

「ならば」に対応する命題を含意(implication)といい、「pならばqである」をp→qと書きます。
含意は条件文とも呼ばれます。

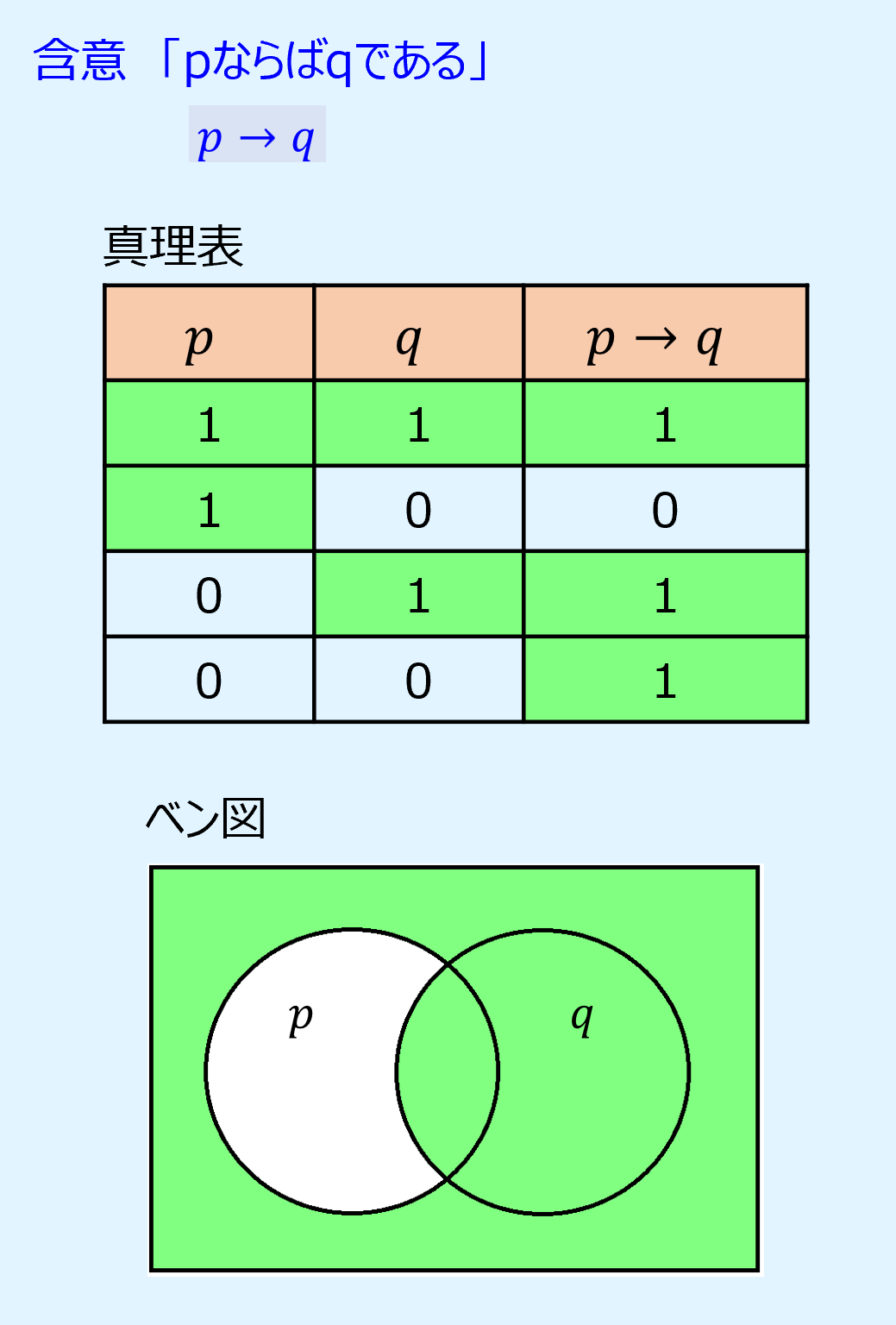
含意は命題pが真で命題qが偽のとき偽、それ以外は真になります。

論理関数の引数と出力の組合せを表形式にしたものを真理値表(truth table)と呼びます。
また、真理値の組合せをベン図で表すこともできます。

以下に含意の真理値表とベン図を示します。

同値「pならばq かつ qならばp」「p↔q」

「pならばqである」 かつ「qならばpである」に対応する命題を同値(equivalence)といい、p↔qと書きます。
同値は双条件文とも呼ばれます。

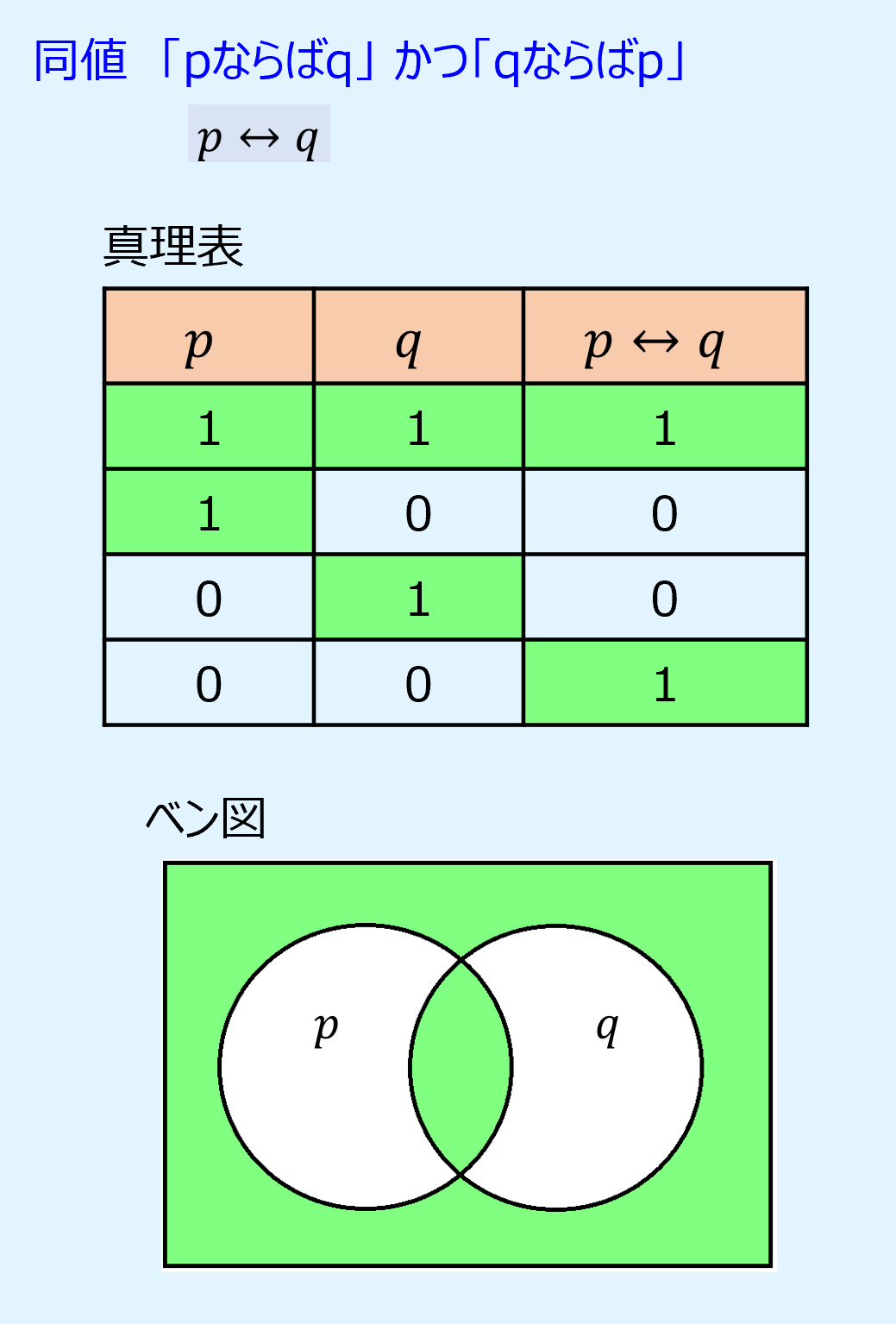
同値は命題p、qの真理値が同じとき真、異なるとき偽となります。

以下に同値の真理値表とベン図を示します。

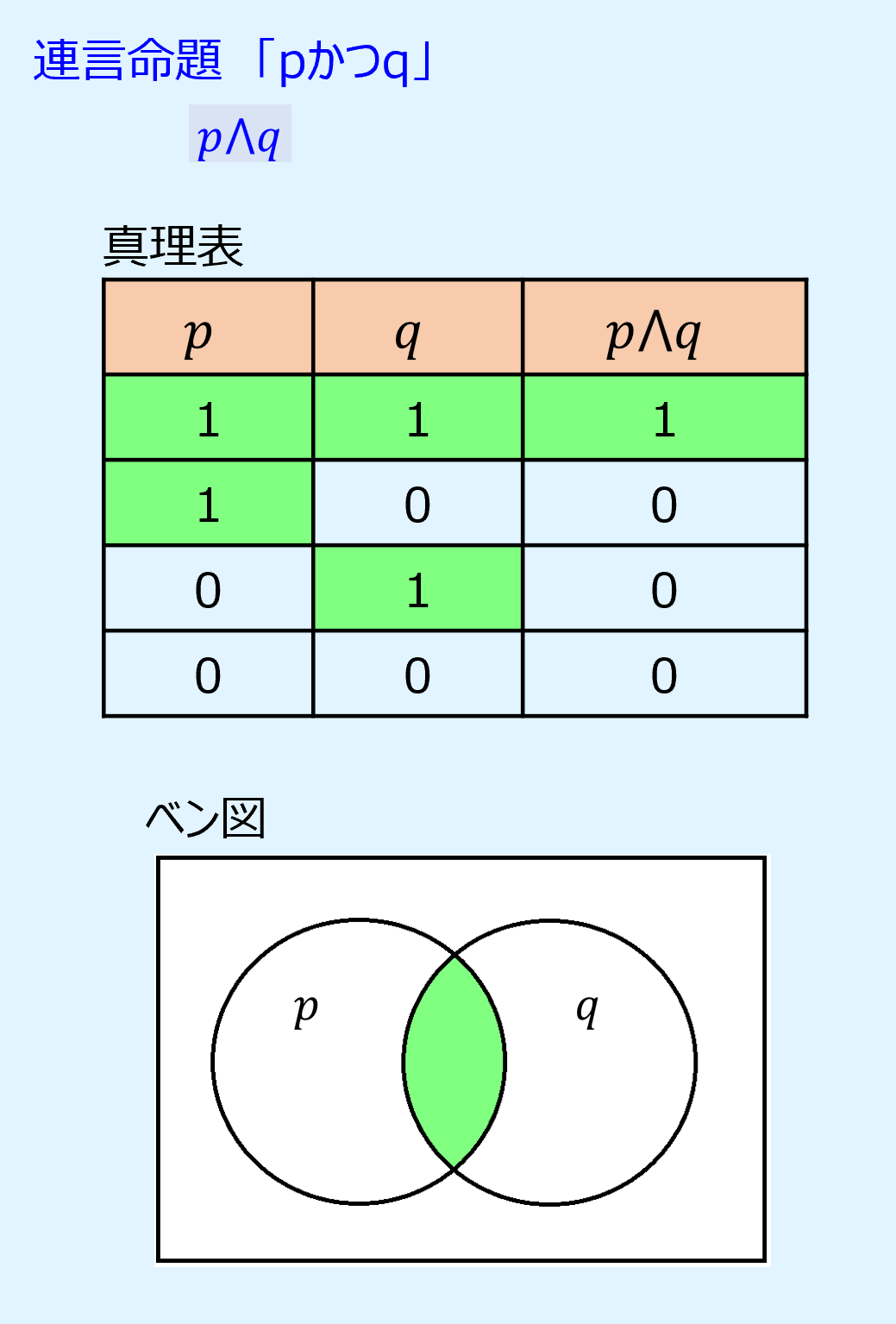
連言命題「pかつq」「p⋀q」

「かつ」に対応する命題を連言命題(conjunctive proposition)といい、p⋀qと書きます。
連言命題は合接命題とも呼ばれます。

連言命題は命題p、qがともに真のとき真、それ以外は偽となります。

以下に連言命題の真理値表とベン図を示します。

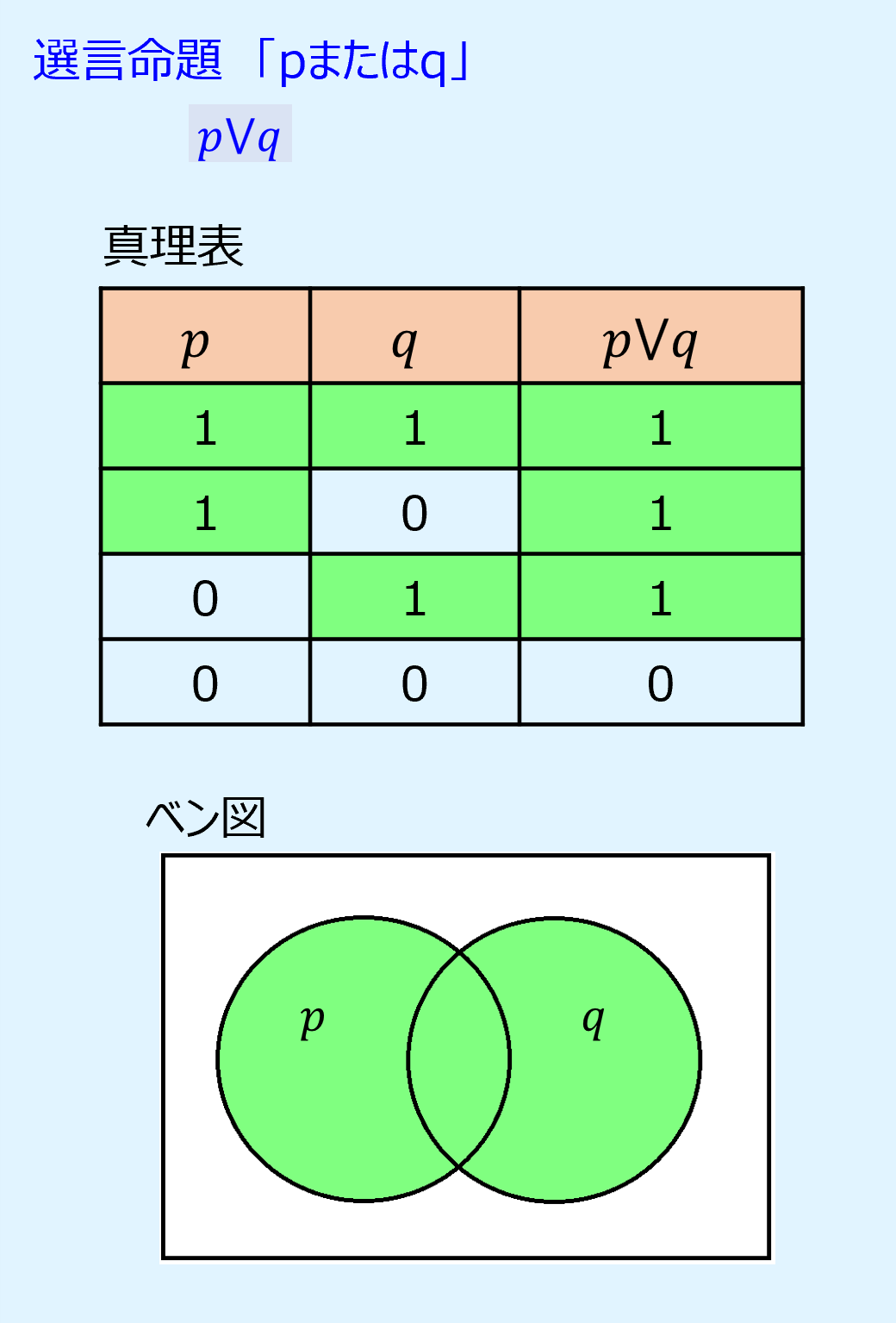
選言命題「pまたはq」「p⋁q」

「または」に対応する命題を選言命題(disjunctive proposition)といい、p⋁qと書きます。
選言命題は隣接命題とも呼ばれます。

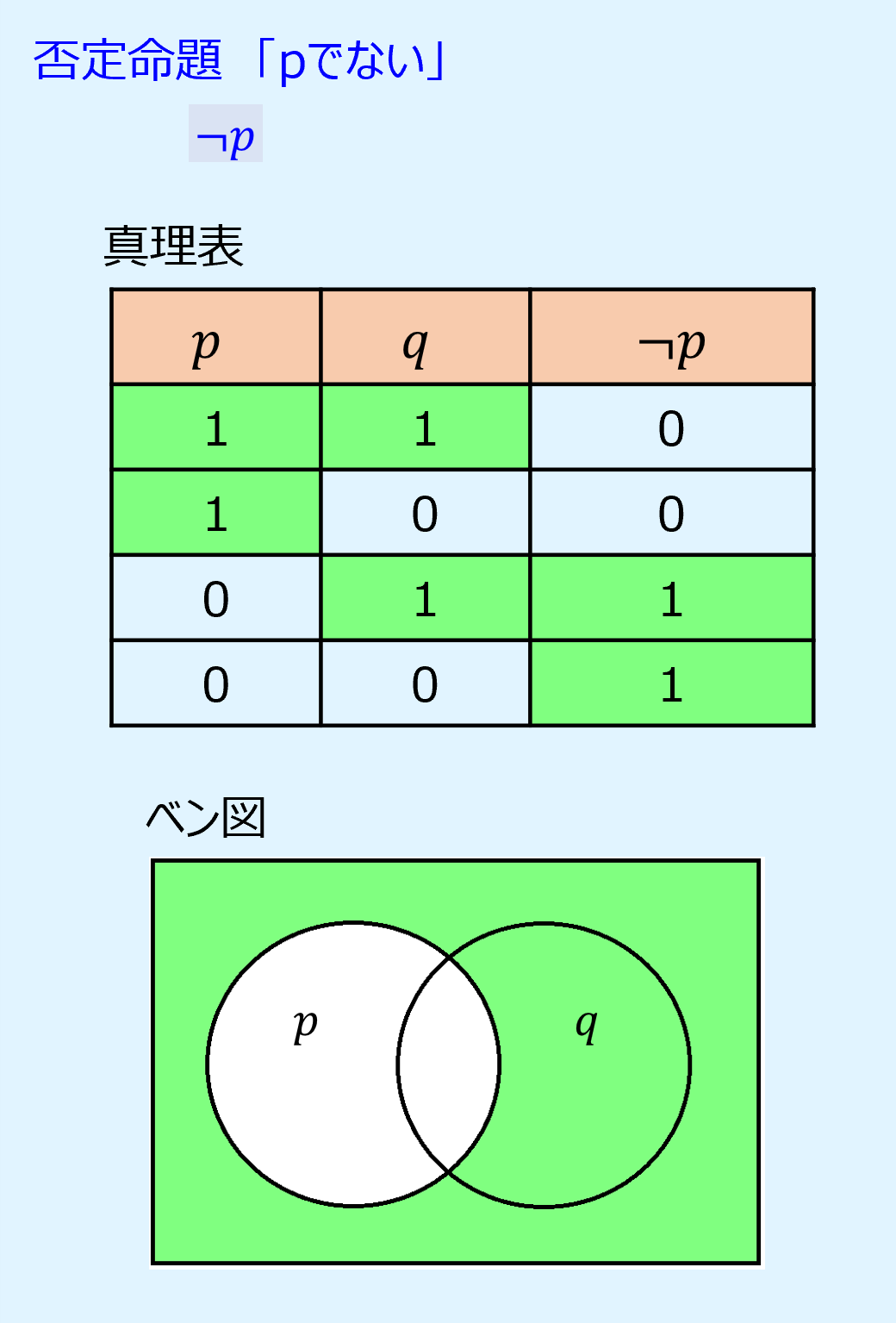
否定命題「pでない」「¬p」

「でない」に対応する命題を否定命題(negative proposition)といい、¬pと書きます。

否定命題は命題pが真であれば偽、偽であれば真となります。

以下に否定命題の真理値表とベン図を示します。