この記事では電気回路で用いられるフェーザ表示での加算と乗算について説明をします。
座標表示との関係から、2つの波形の加算、乗算、N個の波形の加算、乗算まで扱います。
目次
【まとめ】フェーザ表示での加算と乗算
最初にまとめです。
加算、乗算と座標表示の関係
信号の加算を行うのは、複数の信号を合成して一つの信号とする場合です。
例えば複数のセンサからの信号を1つにまとめたりする場合です。
このように信号の加算を行うときの座標表示としては直交座標表示で行います。
一方、信号の乗算を行うのは、別の信号を作り出す場合や信号の変形を行う場合で
- 電圧と電流から電力の計算を行う場合
- 電圧をインピーダンスで割り電流を計算する場合
- アンプやフィルタで振幅の増減、位相の遅延を遅らせる場合
が該当します。
このように信号の乗算を行うときの座標表示としては極座標表示で行います。
フェーザ表示での加算(2つの正弦波の場合)
2つの正弦波を\(v_1\)、\(v_2\)とし、それらを加算して作られる信号を\(v_s\)とすると、それらを複素指数関数を用いた形に変換した\(V_1\)、\(V_2\)、\(V_s\)は以下の関係となります。
ここで、\(\dot{V}_1\)、\(\dot{V}_2\)、\(\dot{V}_s\)は\(V_1\)、\(V_2\)、\(V_s\)のフェーザです。
上式で示す通り、波形の加算は、元のフェーザ\(\dot{V}_1\)、\(\dot{V}_2\)を加算し、合成後のフェーザ\(\dot{V}_s\)を求めるだけとなります。
フェーザの加算は、次式に示すように、実数部と虚数部をそれぞれで足し合わせるだけと容易です。
ここで、\(A_1\)、\(A_2\)は\(\dot{V}_1\)、\(\dot{V}_2\)の実数部、\(B_1\)、\(B_2\)は虚数部です。
フェーザ表示での加算(N個の正弦波の場合)
波形2つの合成なら大したことはないですが、これが3つ、4つ、・・・と増えていくとsinの計算では大変です。
ですが、フェーザ表示なら計算が容易となります。
先の2つの場合を拡張し、フェーザ表示でN個の正弦波を合成すると、以下のようになります。
N個に拡張してもフェーザを加算するだけです。
合成後のフェーザは以下となります。
ここで、ここで、\(A_n\)は\(n\)番目の信号のフェーザ\(\dot{V}_n\)の実数部、\(B_n\)は虚数部です。
直交座標表示から極座標表示への変換
直交座標表示で加算したフェーザを極座標表示に変換するには、次式で実数部と虚数部から振幅\(V_m\)と位相\(varphi\)を求めます。
ここで、\(A\)、\(B\)はフェーザ\(\dot{V}\)の実数部と虚数部、\(N\)は加算した信号数を表します。
また、上式を\(N=2\)とすると以下のようになり、これは別の記事で説明した合成波形の振幅と位相に一致しており、結果が同じであるということが分かります。
フェーザ表示での乗算(2つの成分の場合)
次に乗算をフェーザ表示でどのように計算するのか示します。
まずは2つの成分の場合です。
例として、電圧と電流から電力を求める場合を示します。
ここで\(P\)は瞬時電力\(p\)を複素指数関数に変換したものです。
上式から、乗算の場合でもフェーザの計算を行うだけでよいことが分かります。
電力のフェーザ\(\dot{P}\)は次式で求められます。
極座標表示だと振幅\(P_m\)は\(V_m\)と\(I_m\)の積、位相\(\varphi_p\)は\(\varphi_v\)と\(\varphi_i\)の和で求められます。
次の例として、電流と交流の抵抗であるインピーダンスの積から電圧を求める場合を示します。
インピーダンスのようにそれ自身が正弦波を含んでいなくても、正弦波に対して影響を与える要素もフェーザとすることができます。
電圧のフェーザ\(\dot{V}\)は次式で求められます。
ここでも振幅は総積、位相は総和になっていることが分かります。
ちなみに、電流を求める場合は電圧をインピーダンスで割りますが、その場合、振幅は逆数とし、位相は符号を反転させるだけなので、基本的には変わりません。
フェーザ表示での乗算(N個の成分の場合)
2つからN個に拡張したフェーザ表示での乗算を以下に示します。
N個になってもフェーザを乗算するだけで済みます。
振幅と位相は以下の式で表されます。
振幅は総積、位相は総和となります。
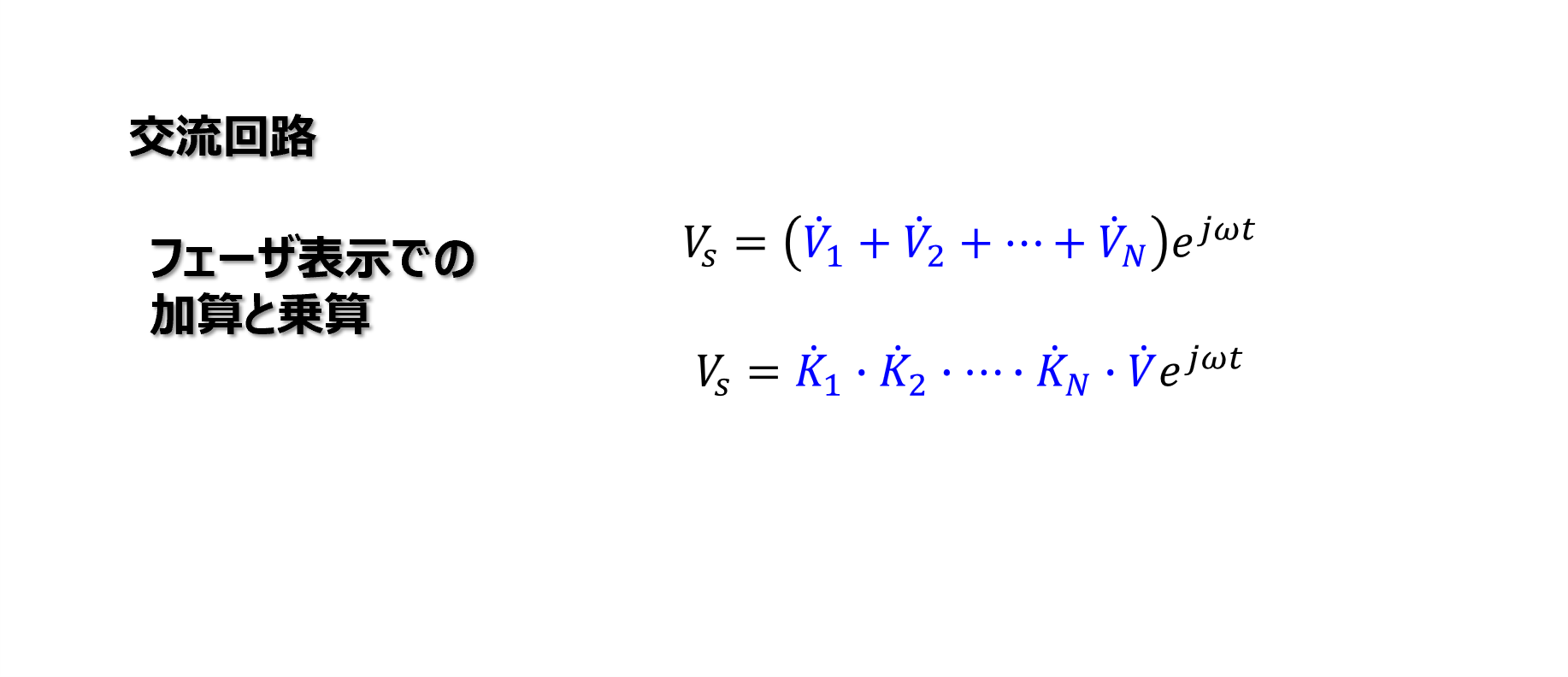

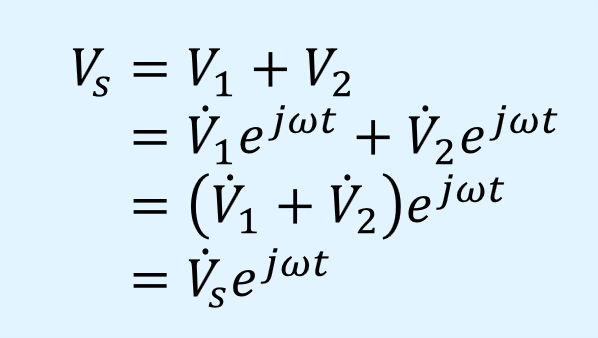
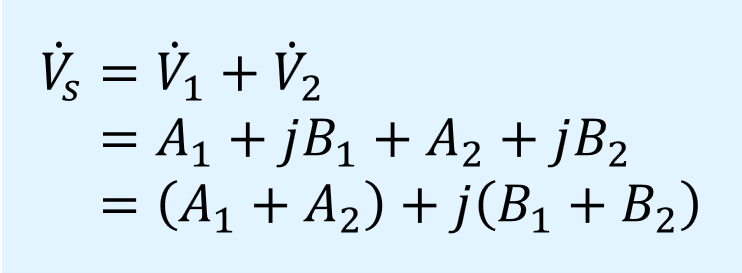
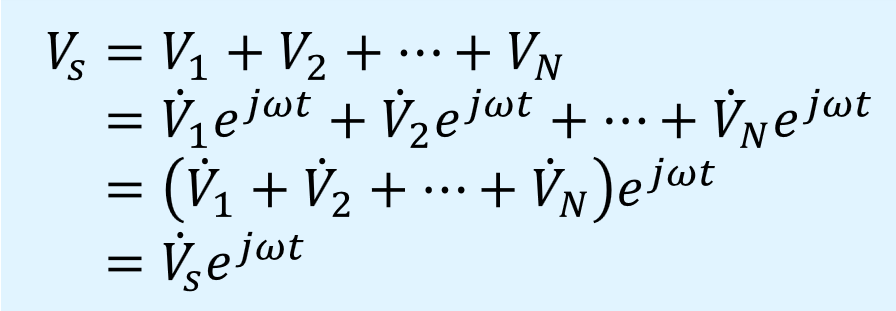
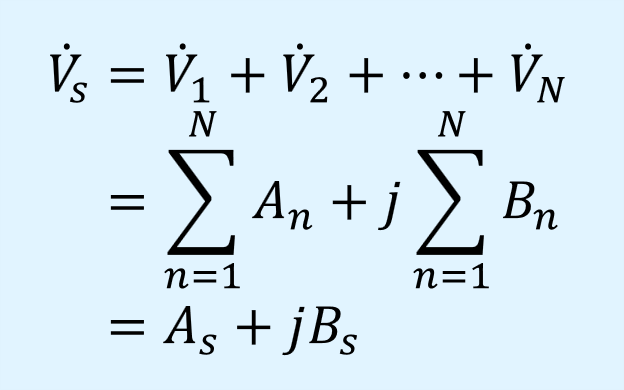
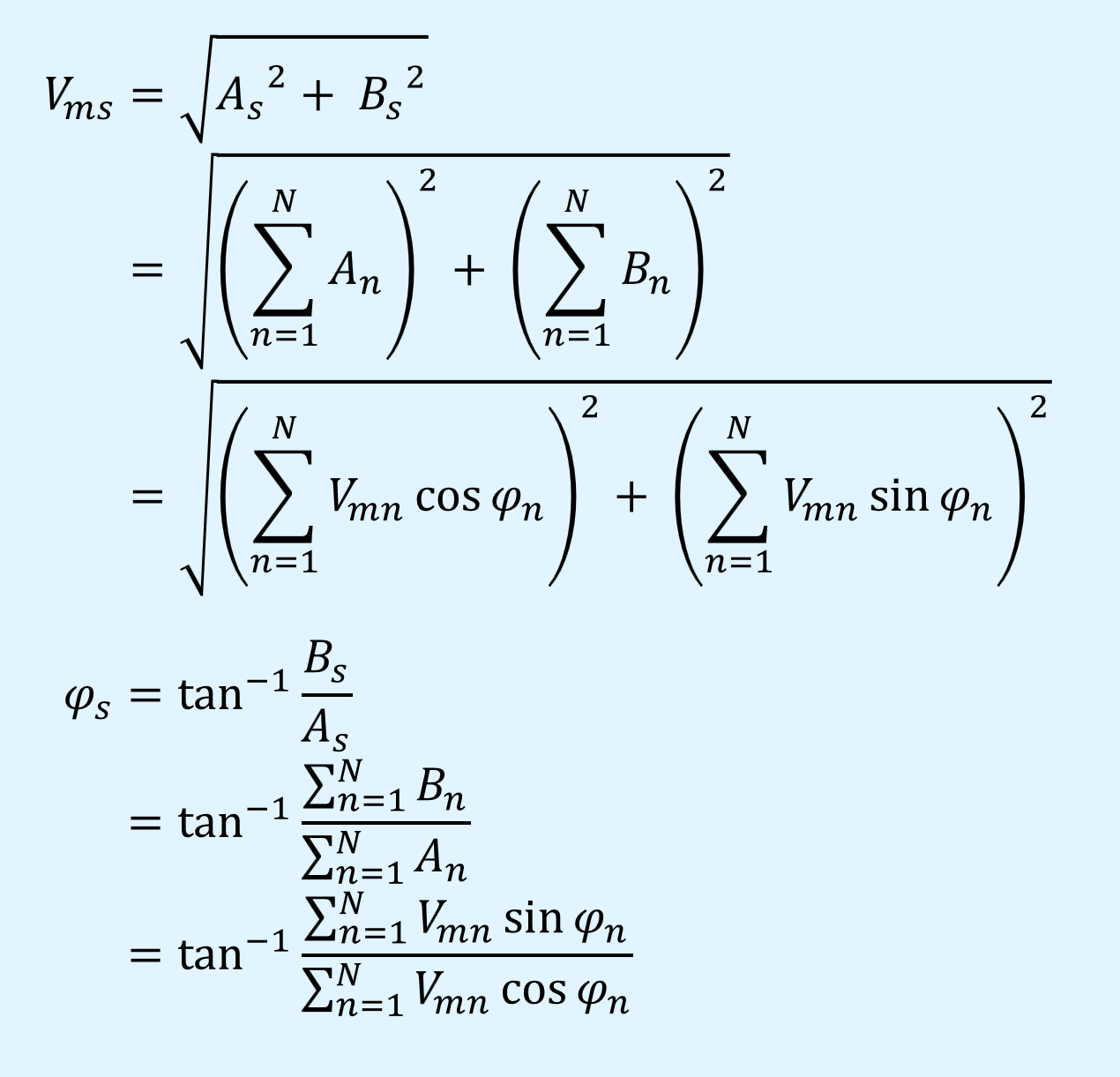
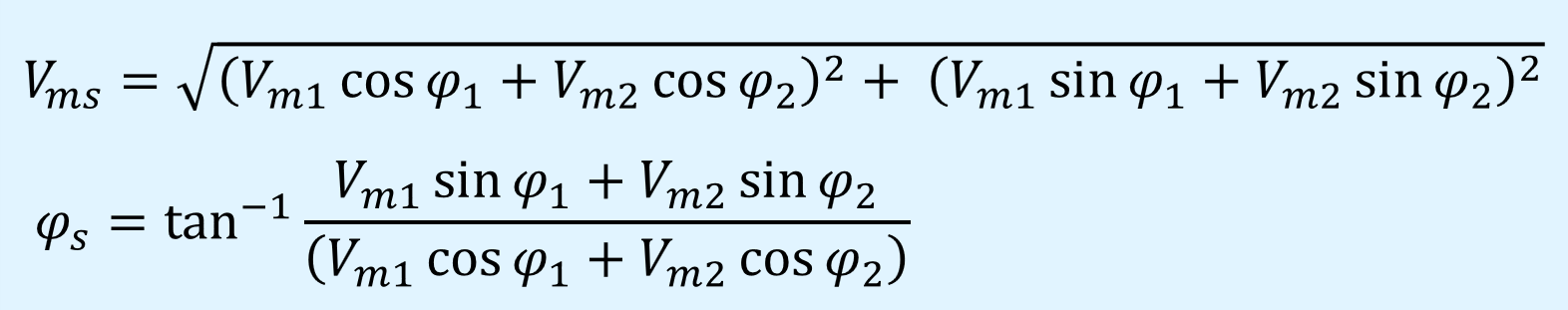
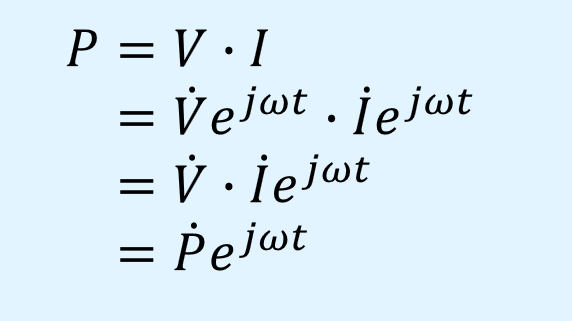
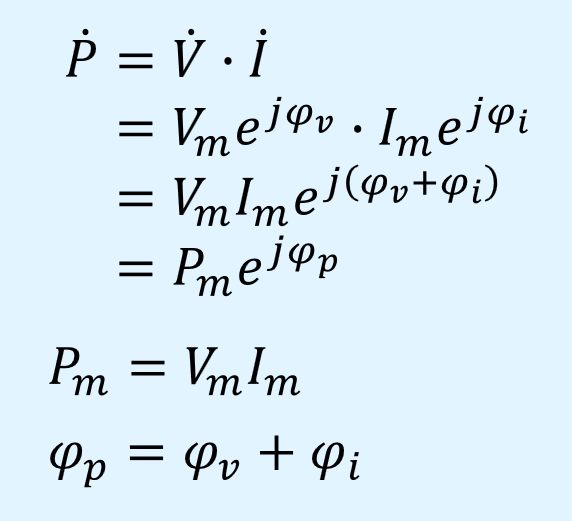
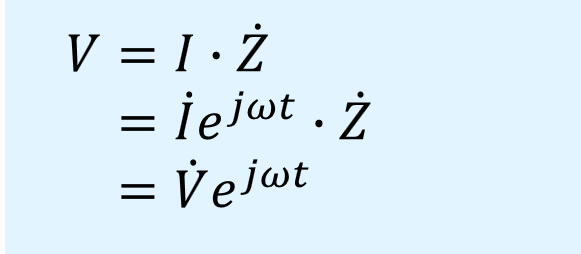
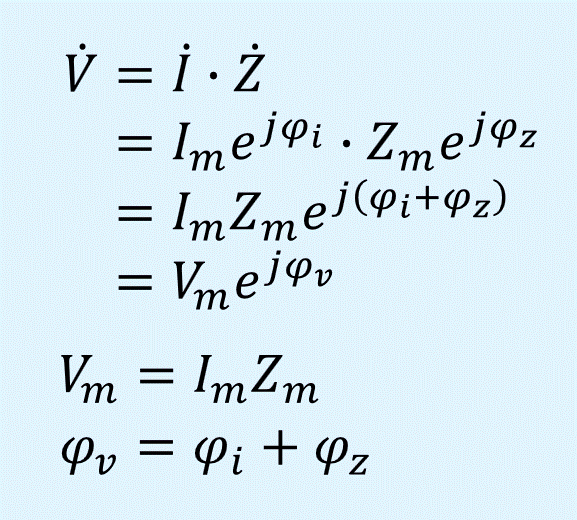

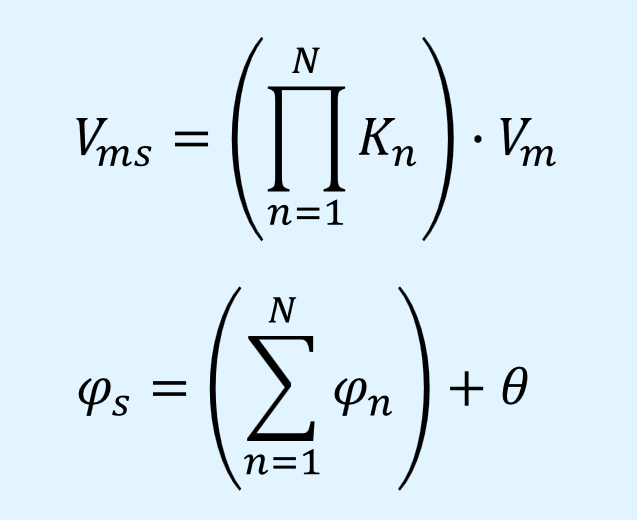


コメント