この記事では電気回路や信号処理で生じる波形の同相と逆相関係について説明をします。
同相と逆相の前に、位相の進みと遅れから説明を始めていきます。
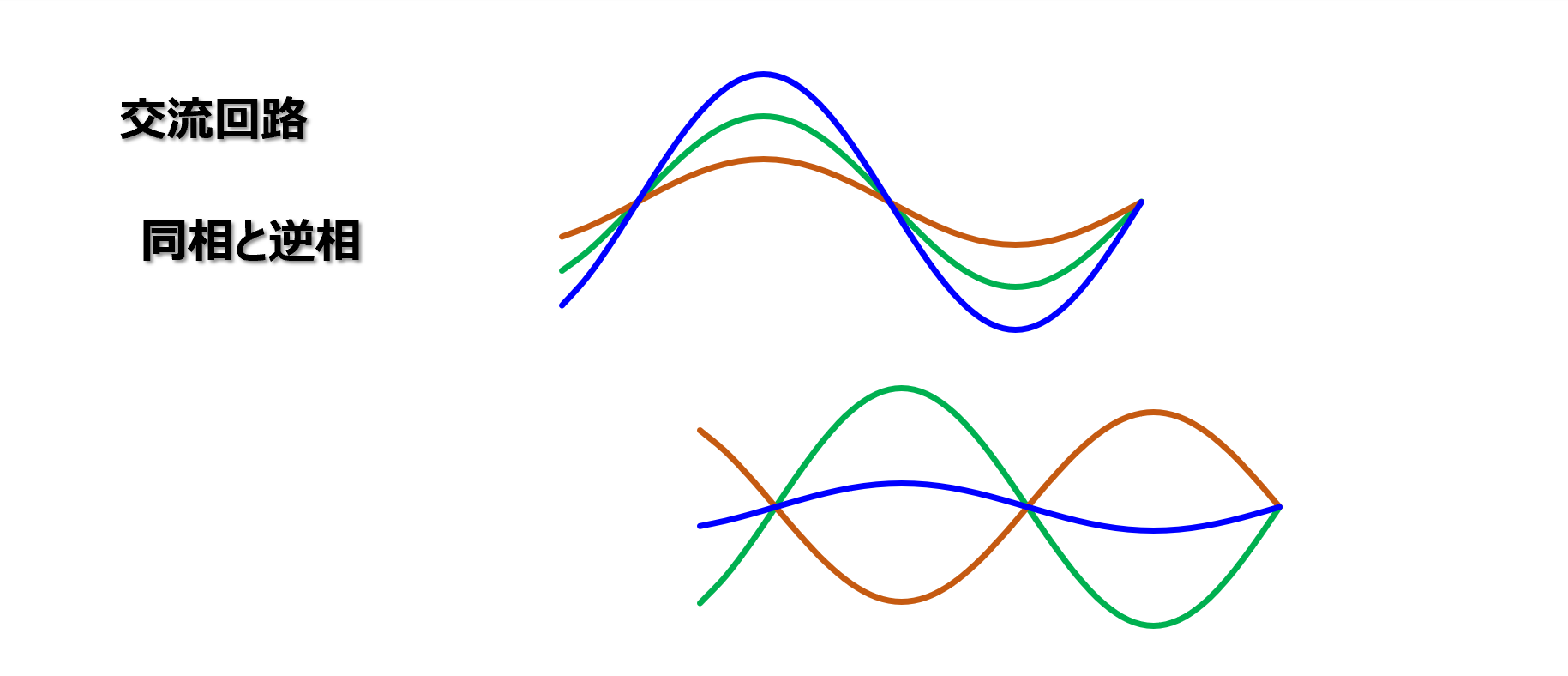
【まとめ】同相と逆相
最初にまとめです。
位相の進みと遅れ
同相と逆相の前に、位相の進みと遅れについて理解をしておきましょう。
基準となる正弦波を以下の式で表します。
この基準に対して、例えば位相を\(\pi/4\)進めるたり、遅らせると以下のようになります。
つまり、位相をプラス方向に増やすと「進んでいる」、マイナス方向に増やすと「遅れている」と表現します。
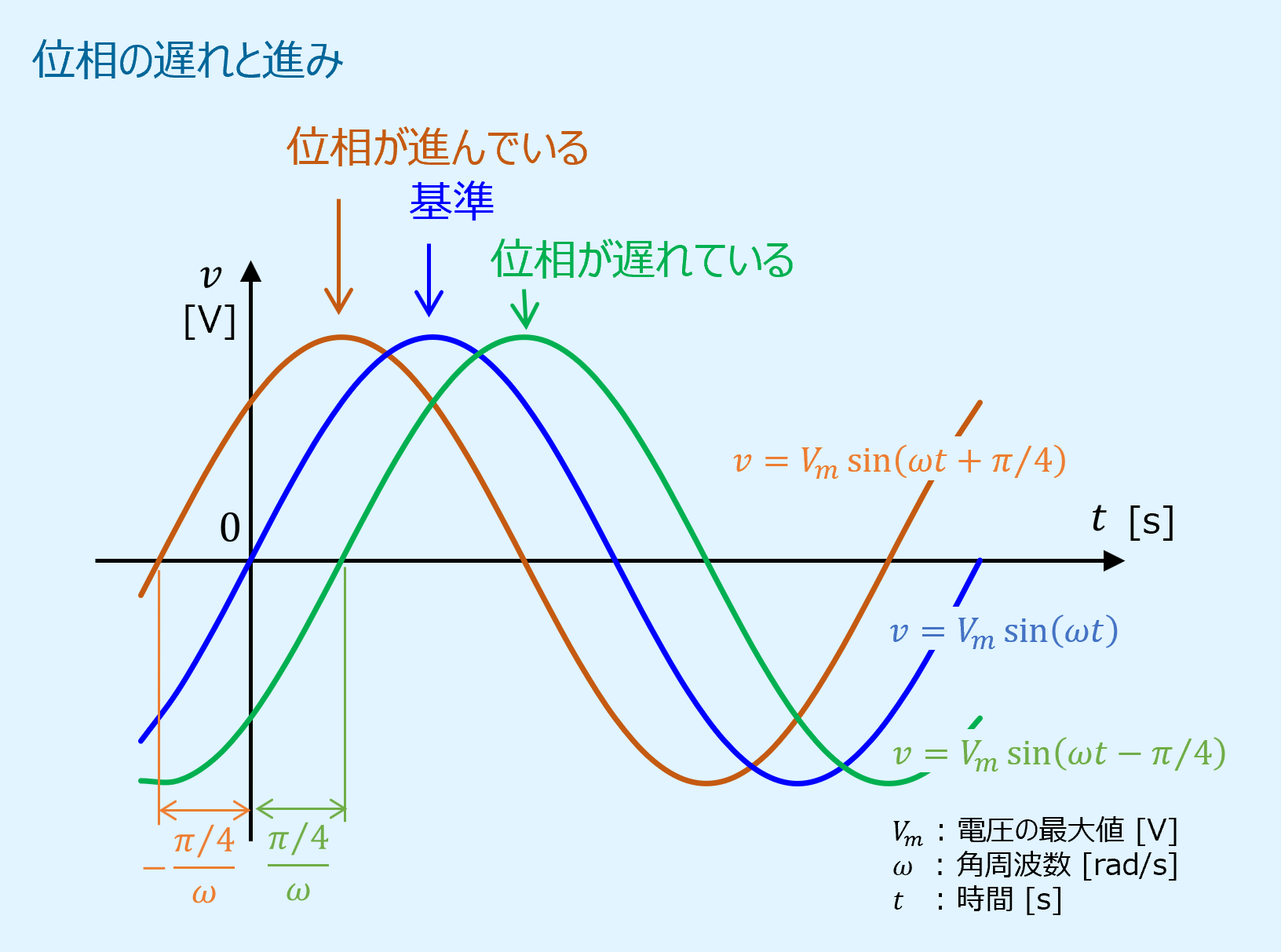
数式だけだと分かりづらいので、以下に時間軸でどうなるのかを示します。
位相の遅れと進みは時間軸を意識した表現で、位相が進んでいる場合は基準よりも早く波形が現れ、遅れている場合は基準よりも遅く波形が現れます。
位相が進んだり遅れたりする原因は複数あります。
電気回路の設計として意図的に位相を変化させる場合もあれば、入力信号に時間差が生じ、その結果として位相が変化する場合もあります。
この後説明する同相と逆相の関係は、この位相の進みと遅れを意図的に操作して作り出すことが多いです。
同相
2つの正弦波に位相差が無い場合、これを同相(in-phase)といいます。
同相の場合、合成波形の振幅と位相は\(\varphi_1=\varphi_2=\varphi\)とおくと次のようになります。
振幅は元の信号の単純加算となり、互いに強め合う関係となります。
すなわち、必要な信号については同相となるように電気回路等で位相を進めたり遅らせたりします。
また、当然ですが位相は元の信号と同じになります。
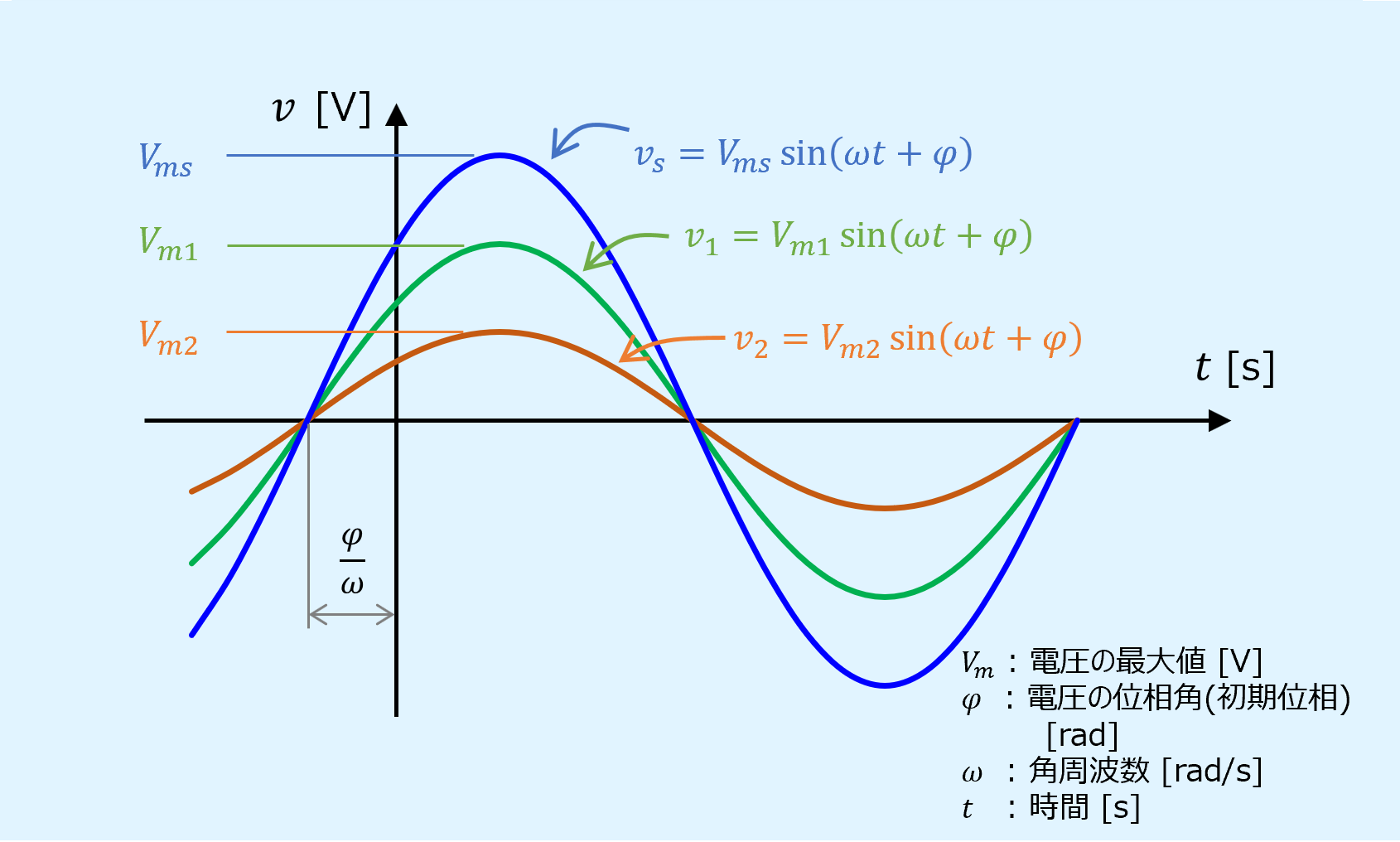
このことを図示すると以下となります。
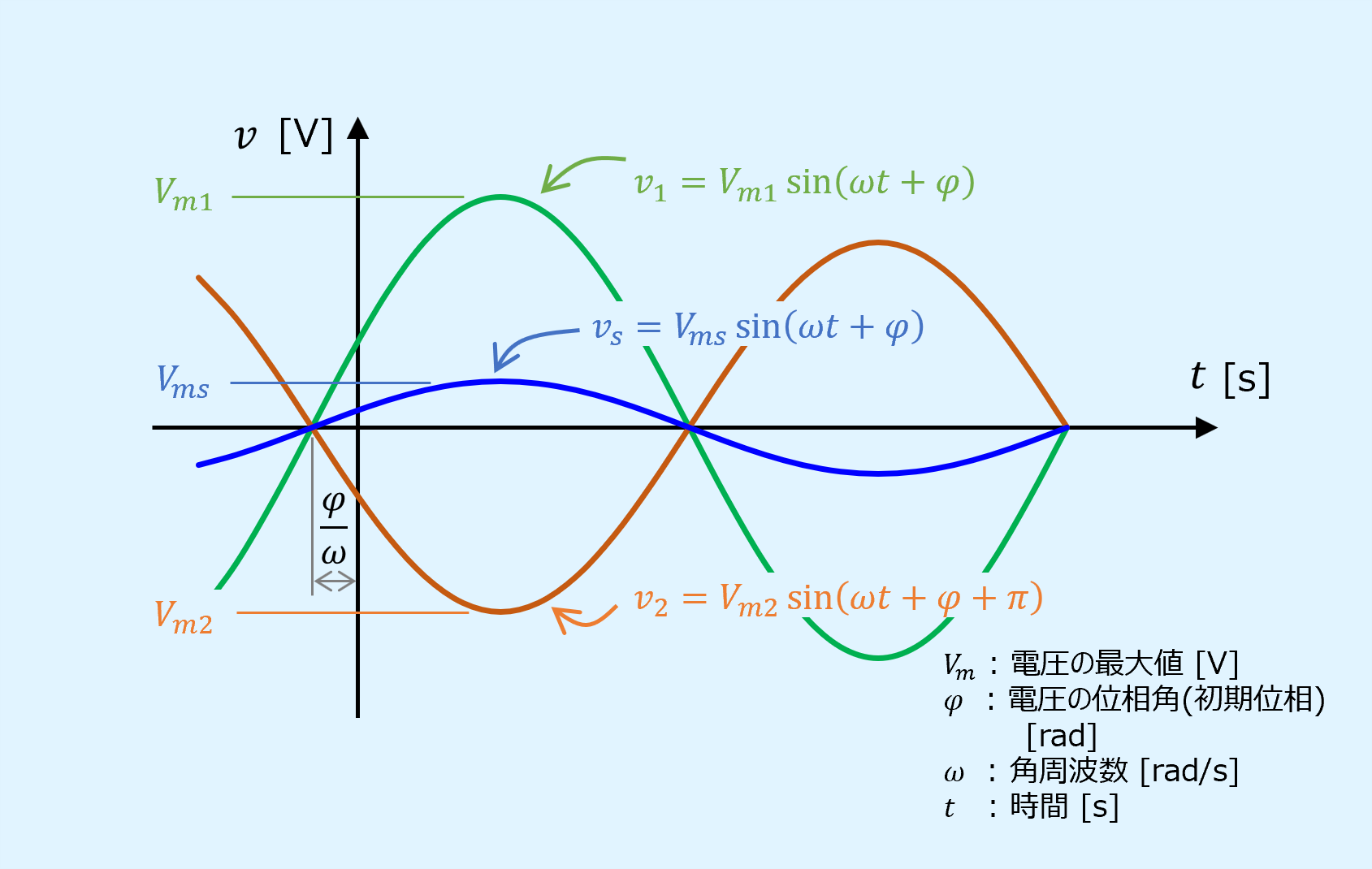
逆相
2つの正弦波に位相差が無い場合、これを逆相(anti-phase)といいます。
逆相の場合、合成波形の振幅と位相は、2つの正弦波の位相を、\(\varphi_2=\varphi+\pi\)とおくと次のようになります
振幅は元の信号同士の差分となり、互いに打ち消しあう関係となっています。
すなわち、不要な信号については逆となるように電気回路等で位相を進めたり遅らせたりします。
また、出力を一定に保つためにフィードバックを掛ける場合も逆相となるようにし、発振を起こさないようにしています。
また、位相は\(\varphi\)ですが、\(V_{m1}<V_{m2}\)の場合は振幅が負となりますので、位相が反転した\(-\varphi\)であることと同じになります。
このことを図示すると以下となります。



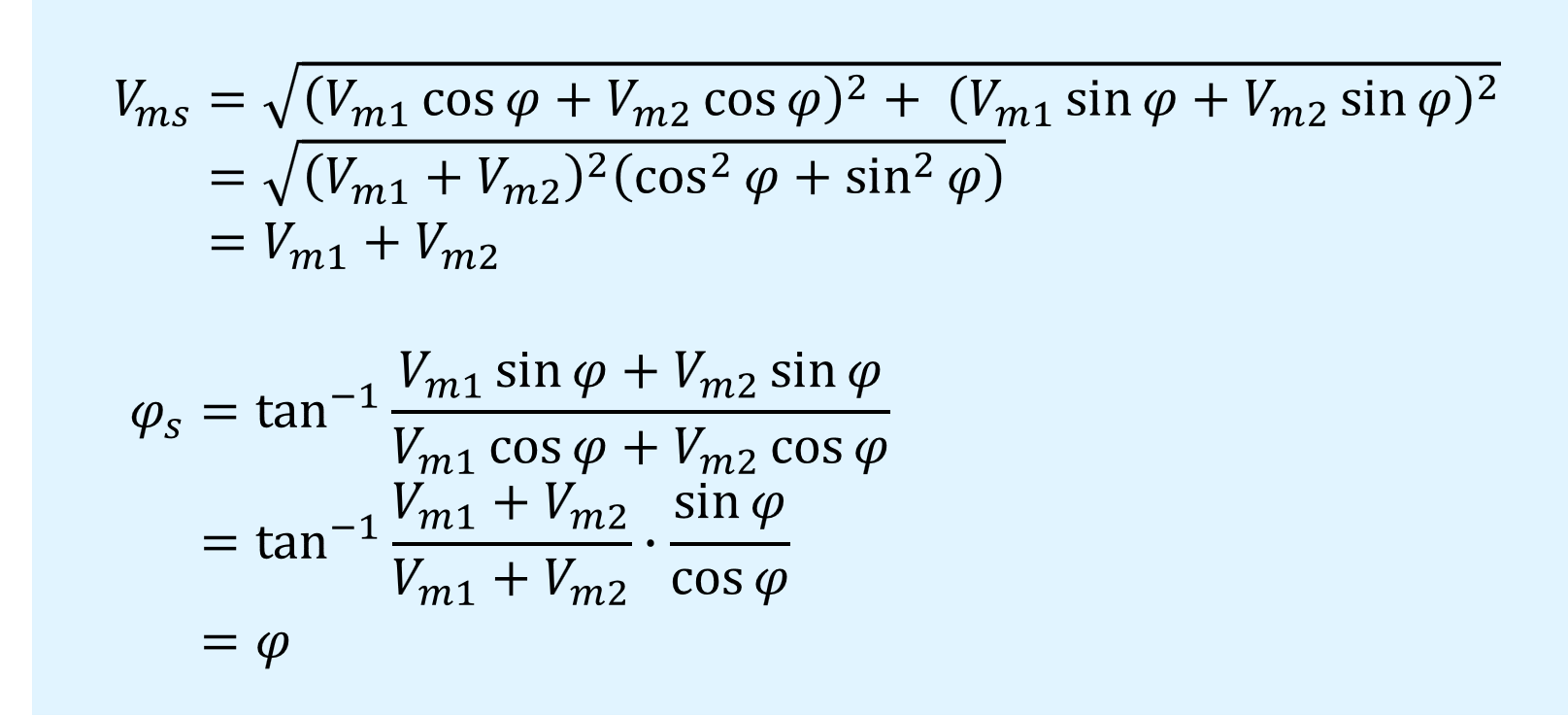



コメント