この記事では電気回路の一つである直流回路について、演習問題の解説をします。
電圧源が1つ、抵抗3つ以上から成る回路の電流値or抵抗値を求めます。
解説用の回路
演習問題の前に、対象となる回路の解説を行います。
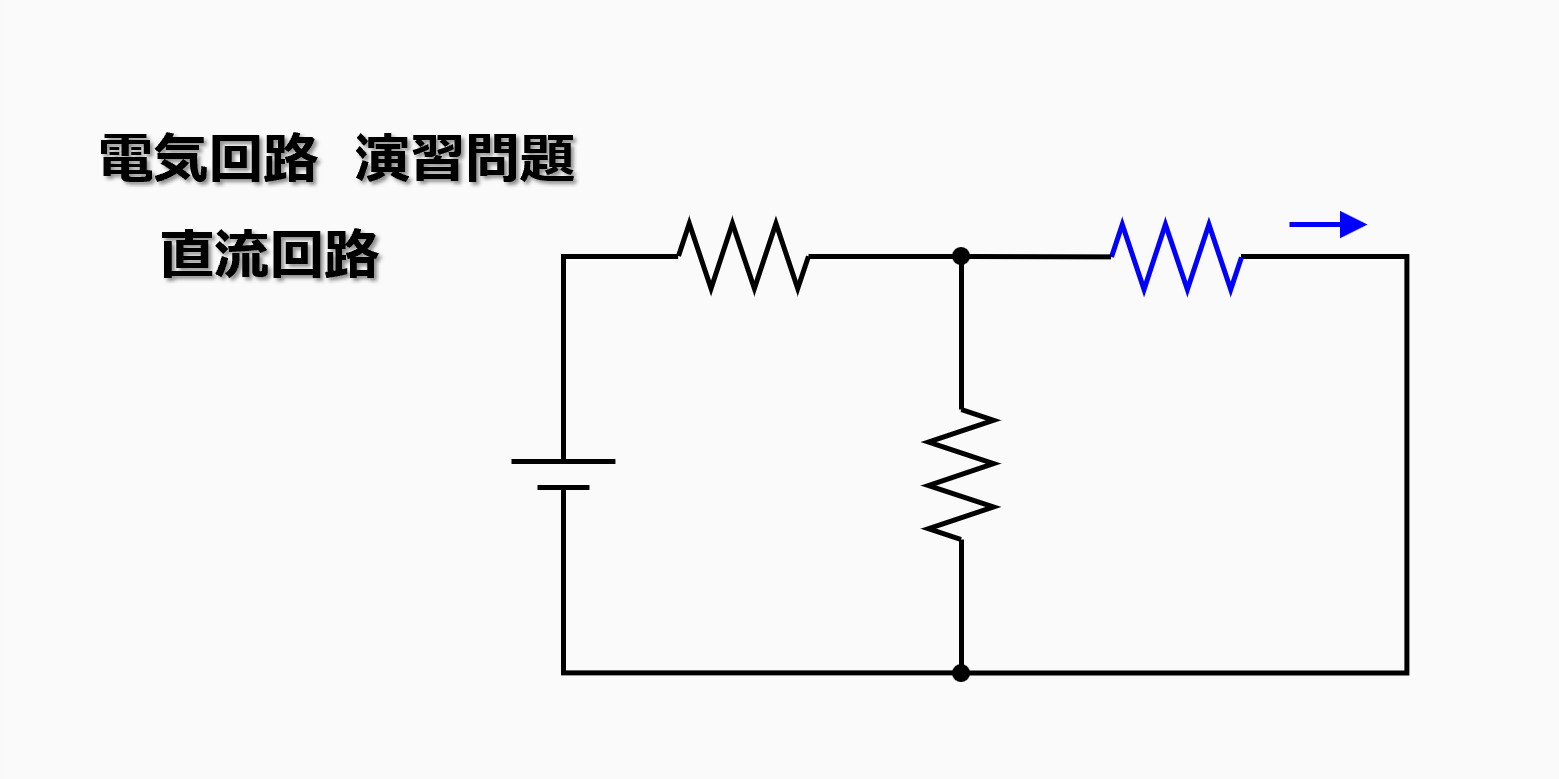
解説用の回路は以下となります。
電圧源1つ、抵抗3つから成る回路です。
ここで求めるのは\(R_3\)、または\(R_3\)の枝に流れる電流\(I_3\)です。
解法は、合成抵抗計算とオームの法則のみ、分圧比も用いる、キルヒホッフの法則を用いる、の3つとなります。
解法1:合成抵抗計算とオームの法則のみ
合成抵抗の計算を行い、全体の電流を計算してから、各部の電圧、電流を計算します。
合成抵抗の計算は、直列接続の合成→並列接続の合成→直列接続の合成、と繰り返していきます。
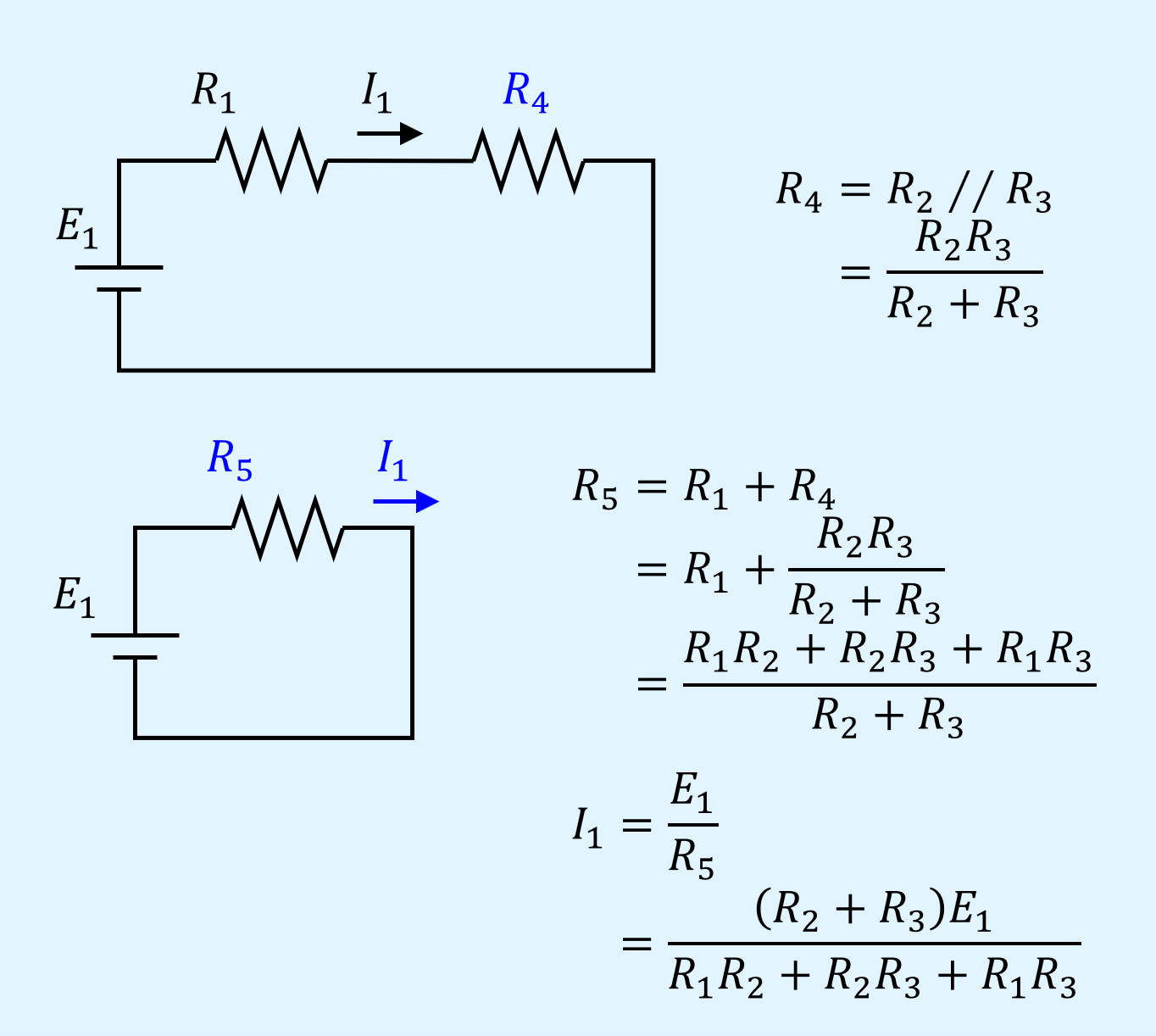
上記の回路では、まず\(R_2\)と\(R_3\)の並列接続を合成し、その合成結果の\(R_4\)と\(R_1\)の直列接続の合成を行い、全体の合成抵抗\(R_5\)を求めます。
\(R_5\)で電源電圧\(E_1\)を割ると、回路全体に流れる電流\(I_1\)が求まります。
\(R_3\)を求めたい場合、電流\(I_1\)の式を変形すると求まります。
\(I_3\)を求めたい場合、電流\(I_1\)から\(R_4\)に印加される電圧\(V_4\)を出し、\(V_4\)を\(R_3\)で割ることで求めます。
解法2:分圧比を用いる
抵抗の比が電圧の分圧比になることを利用します。
並列接続されている\(R_2\)と\(R_3\)の合成抵抗\(R_4\)を求めたら、\(R_1\)との合成抵抗を出し、\(R_4\)との比で電圧\(V_4\)を出します。
後はオームの法則より\(R_3\)、\(I_3\)を算出します。
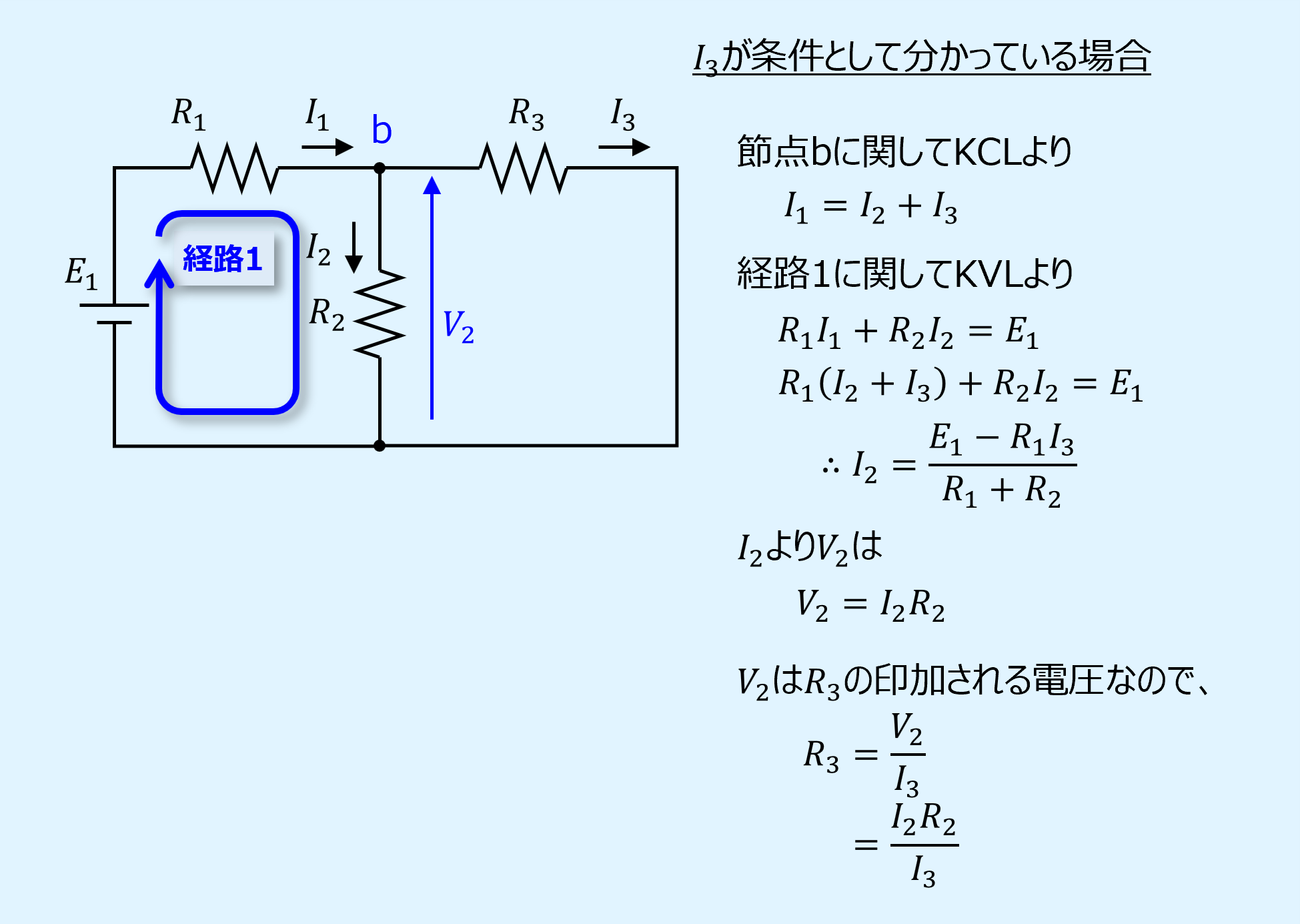
解法3:キルヒホッフの法則を用いる
\(I_3\)が事前の条件として分かっている場合、キルヒホッフの法則より\(R_3\)を求めることができます。
演習問題1
電圧源1つ、抵抗4つから成る直流回路の問題を以下に示します。
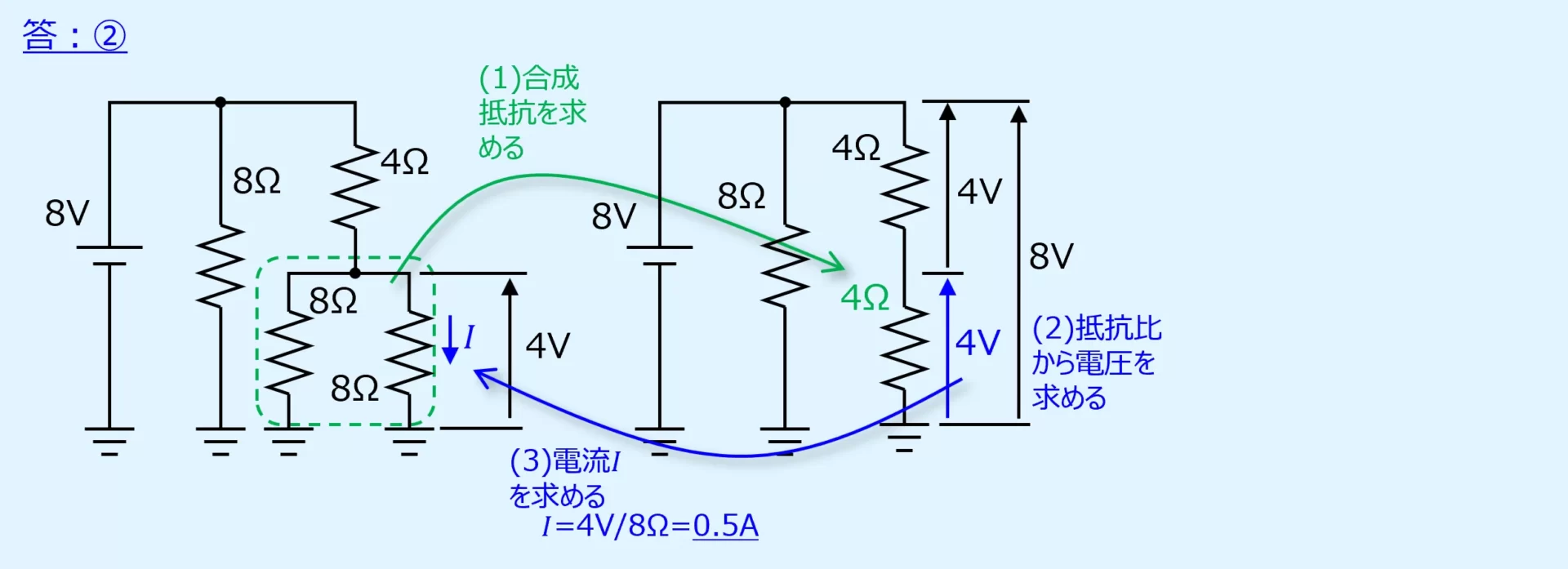
未知の電流Iの値を求めます。
合成抵抗計算と分圧比から解きます。
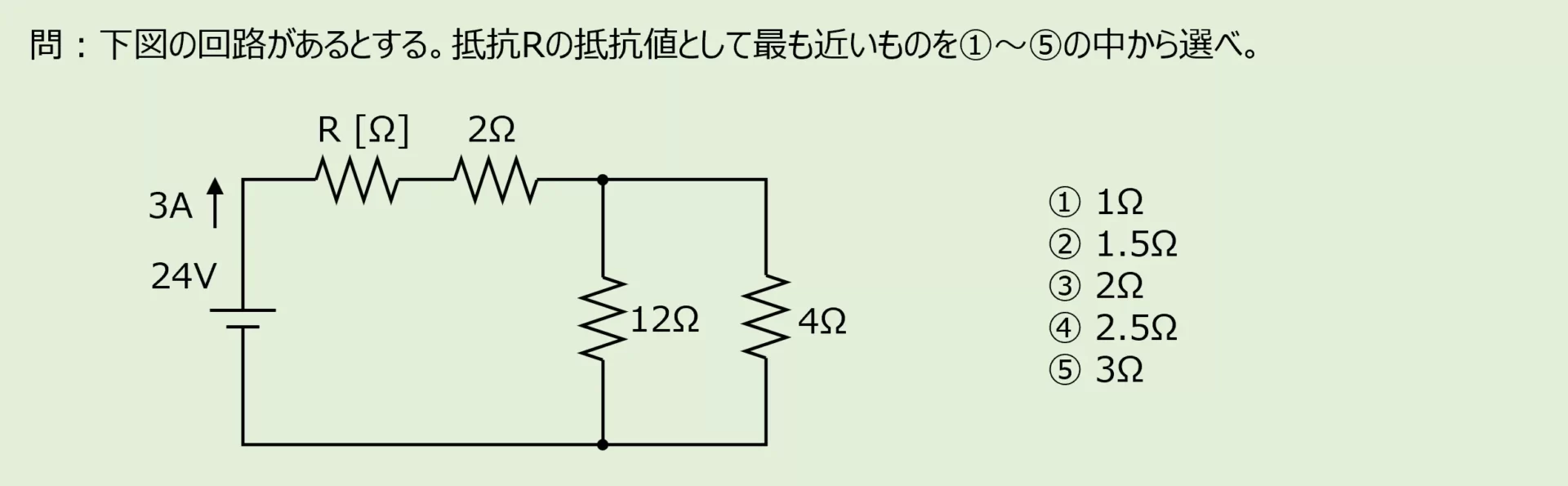
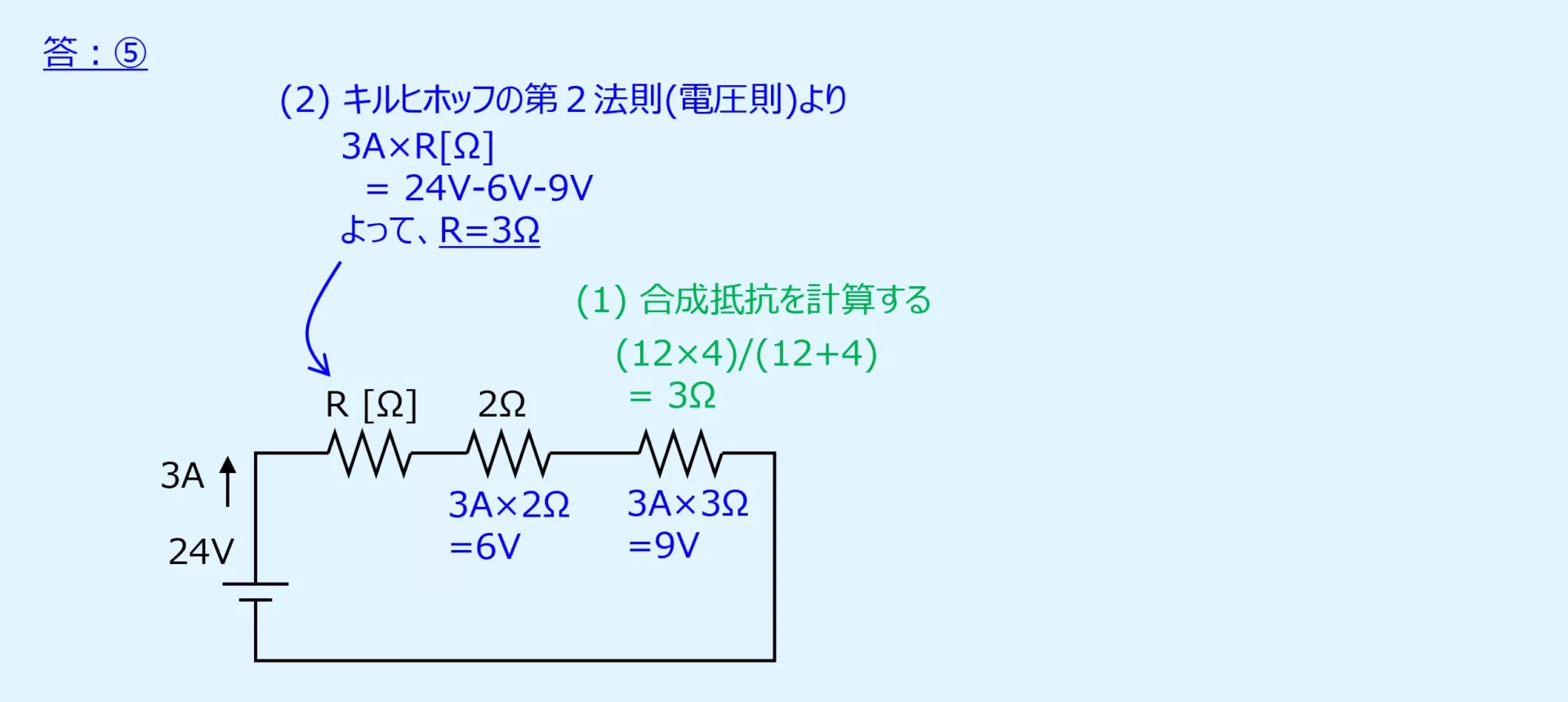
演習問題2
電圧源1つ、抵抗4つから成る直流回路の問題を以下に示します。
未知の抵抗Rの値を求めます。
キルヒホッフの法則を用いて解きます。
その他
電気回路全般については以下をご覧下さい。







コメント