この記事では数学や情報処理で用いられる集合ついて説明をします。
集合であることの条件や集合の表現方法を取り扱います。
【まとめ】集合
最初にまとめです。
集合とは
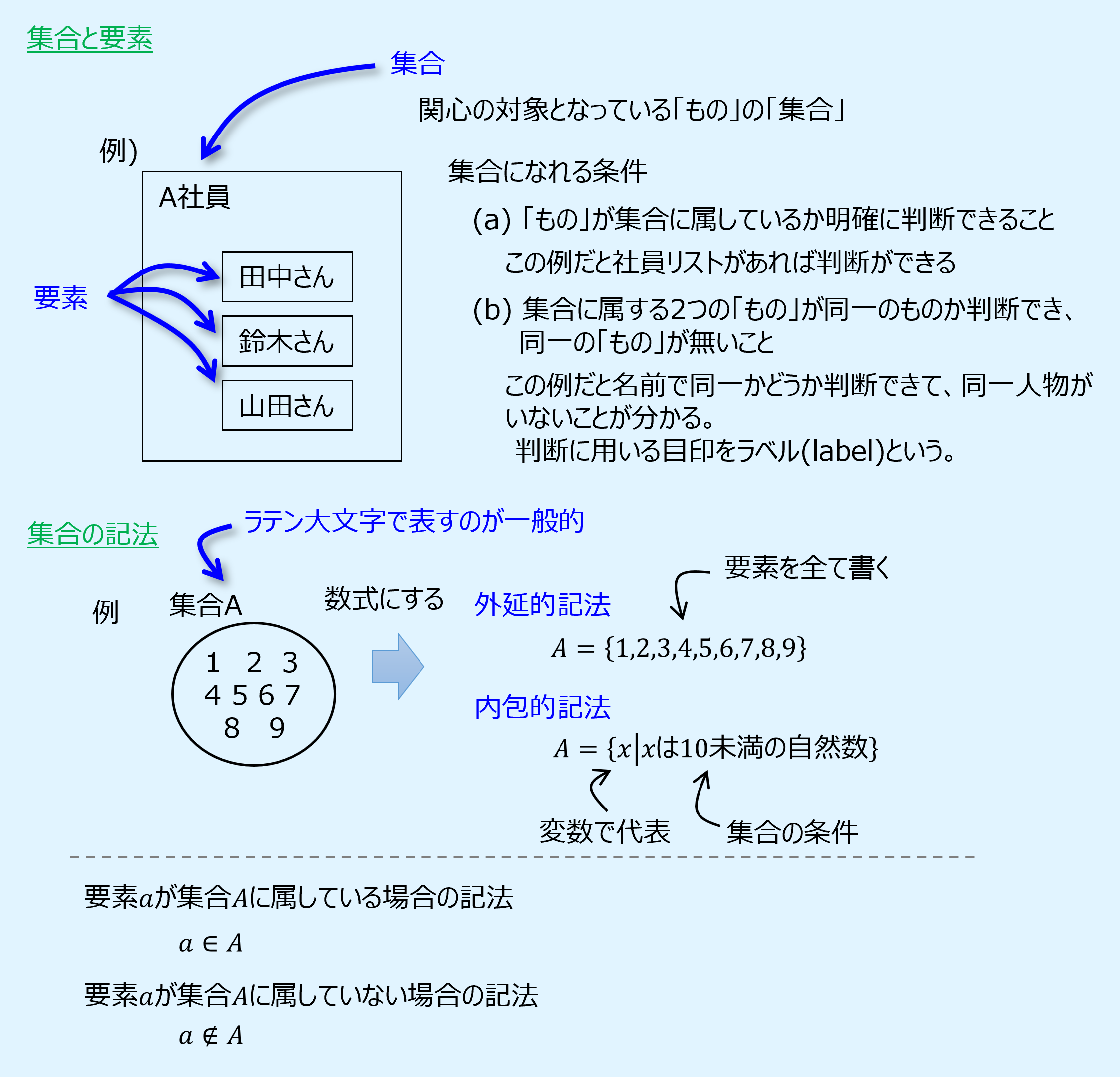
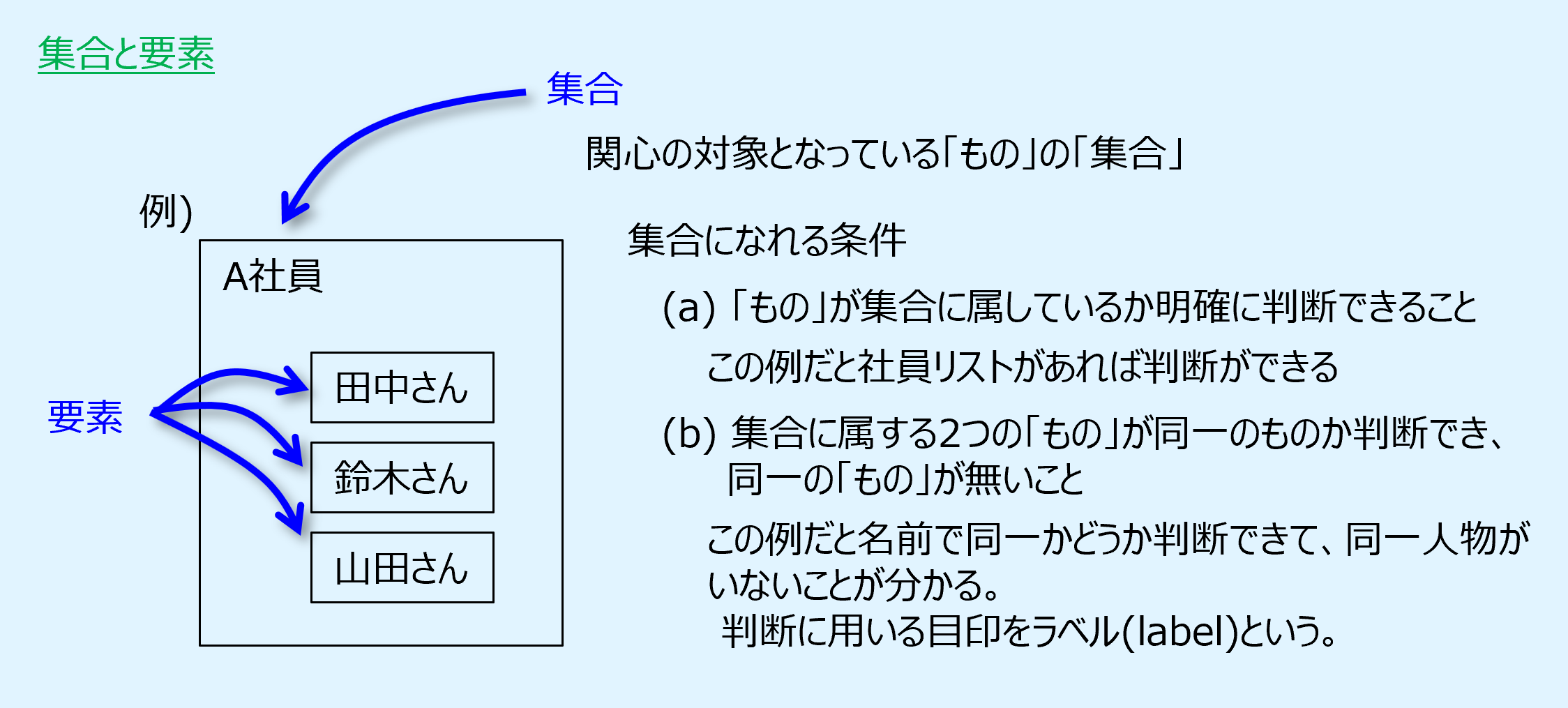
集合(Set)とは、関心の対象となっている「もの」の「集まり」のことです。
かつ以下の条件を満たします。
(a) 「もの」が集合に属するかどうか明確に判断できること。
(b) 集合に属する2つの「もの」が同一のものか判断でき、同一の「もの」が無いこと。
____(「もの」の重複を許す集合は多重集合と呼ばれる)
集合に属する「もの」のことを要素または元(element)と呼びます。
以下に集合と要素の例を示します。
集合の表現方法
集合は、A,B,・・・,M,N,・・・X,Y,・・・などのラテン大文字で表されるのが一般的です。
ただし、
- N : 自然数全体の集合
- Z : 整数全体の集合
- Q : 有理数全体の集合
- R : 実数全体の集合
- C : 複素数全体の集合
で使われることが一般的ですので、混在しないように注意しましょう。
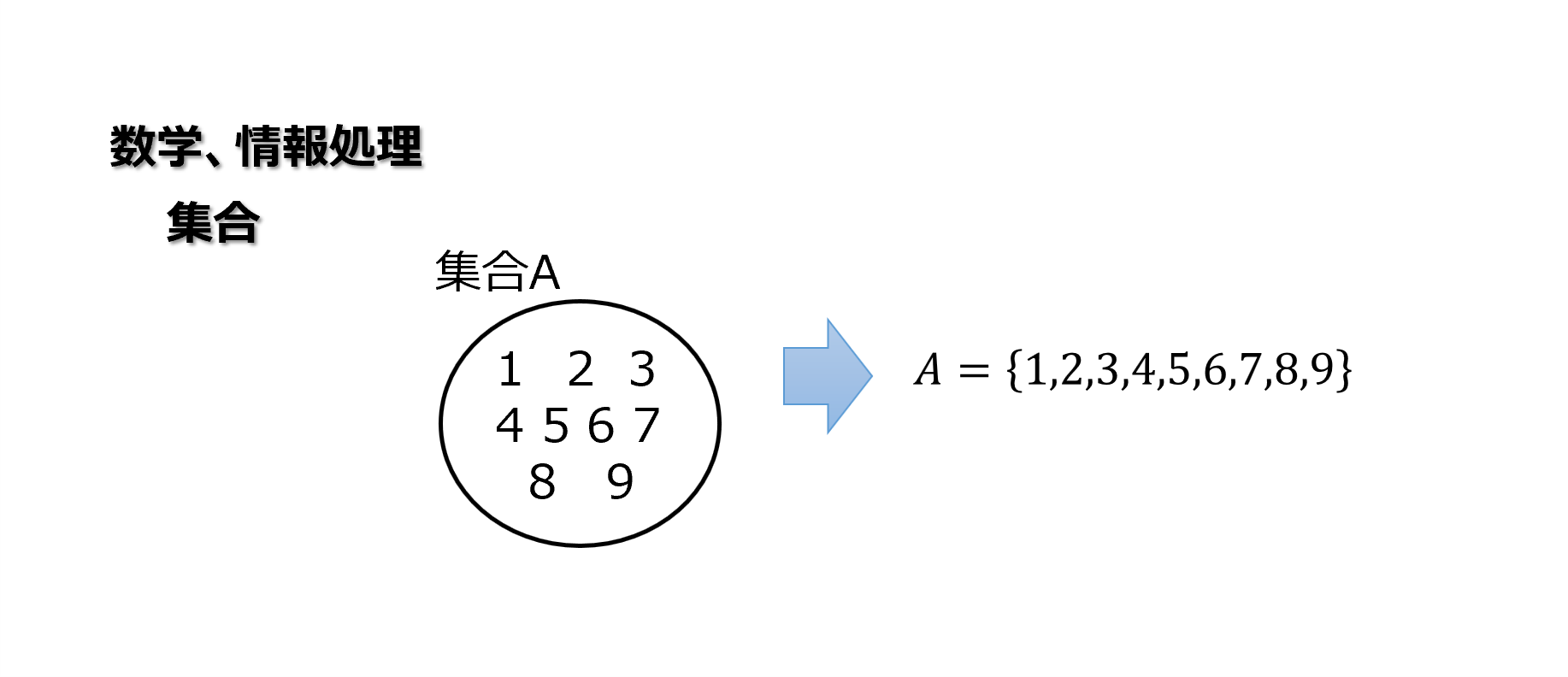
集合の記法
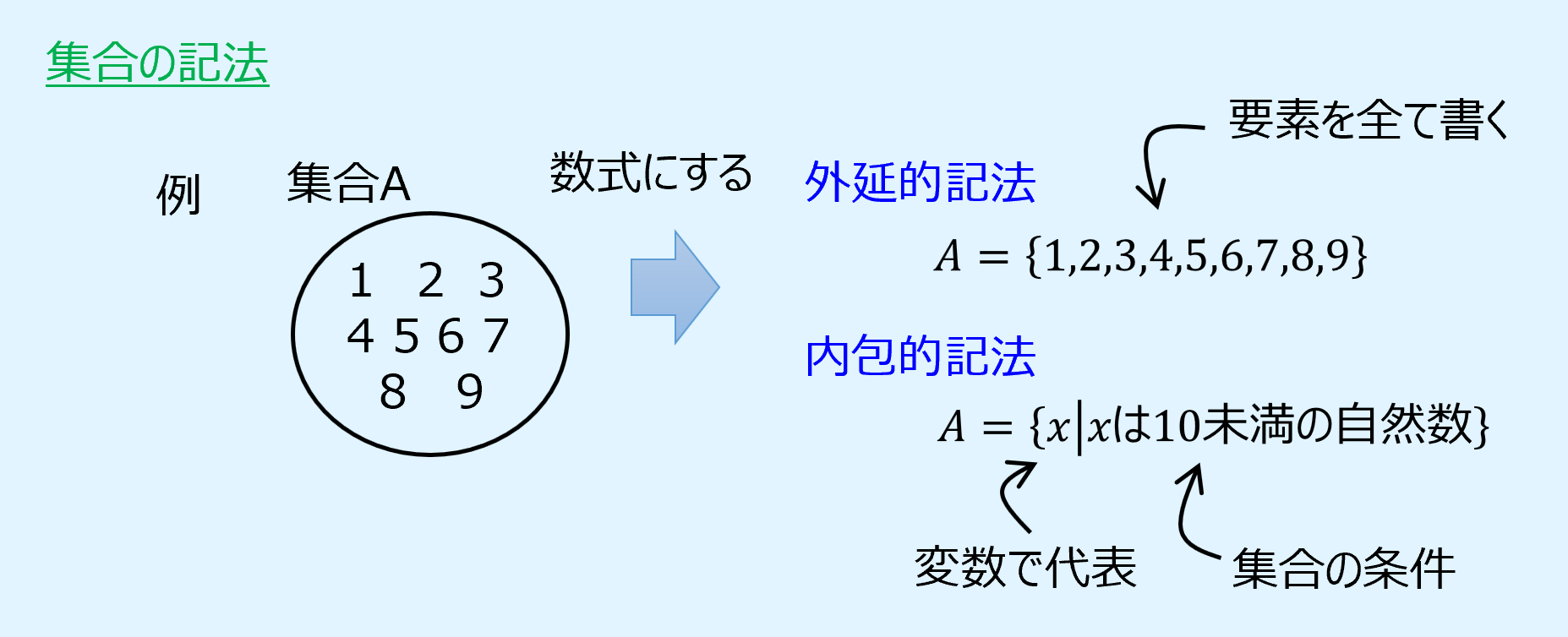
集合の記法には外延的記法(denotation)と内包的記法(connotation)があります。
- 外延的記法(枚挙法とも呼ぶ):
要素を「,」で区切って全て並べ、全体を{}で囲む。 - 内包的記法:
要素は変数で代表して記載し、「|」で区切った横に変数の条件を記載する。
以下に外延的記法と内包的記法の例を示します。
ここで、記号「=」を用いていますが、これは左辺と右辺の集合の要素が互いに全て同じであることを意味しています。
また、要素\(a\)が集合\(A\)に属している場合以下のように記載します。
逆に、要素\(a\)が集合\(A\)に属していない場合以下のように記載します。

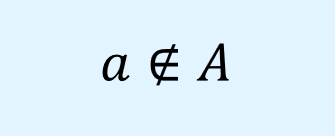

コメント