この記事では電気回路の一種であるRL直列直流回路のスイッチをONにした時に起きる過渡現象について取り扱います。
電流の式導出と電流の時間特性について説明します。
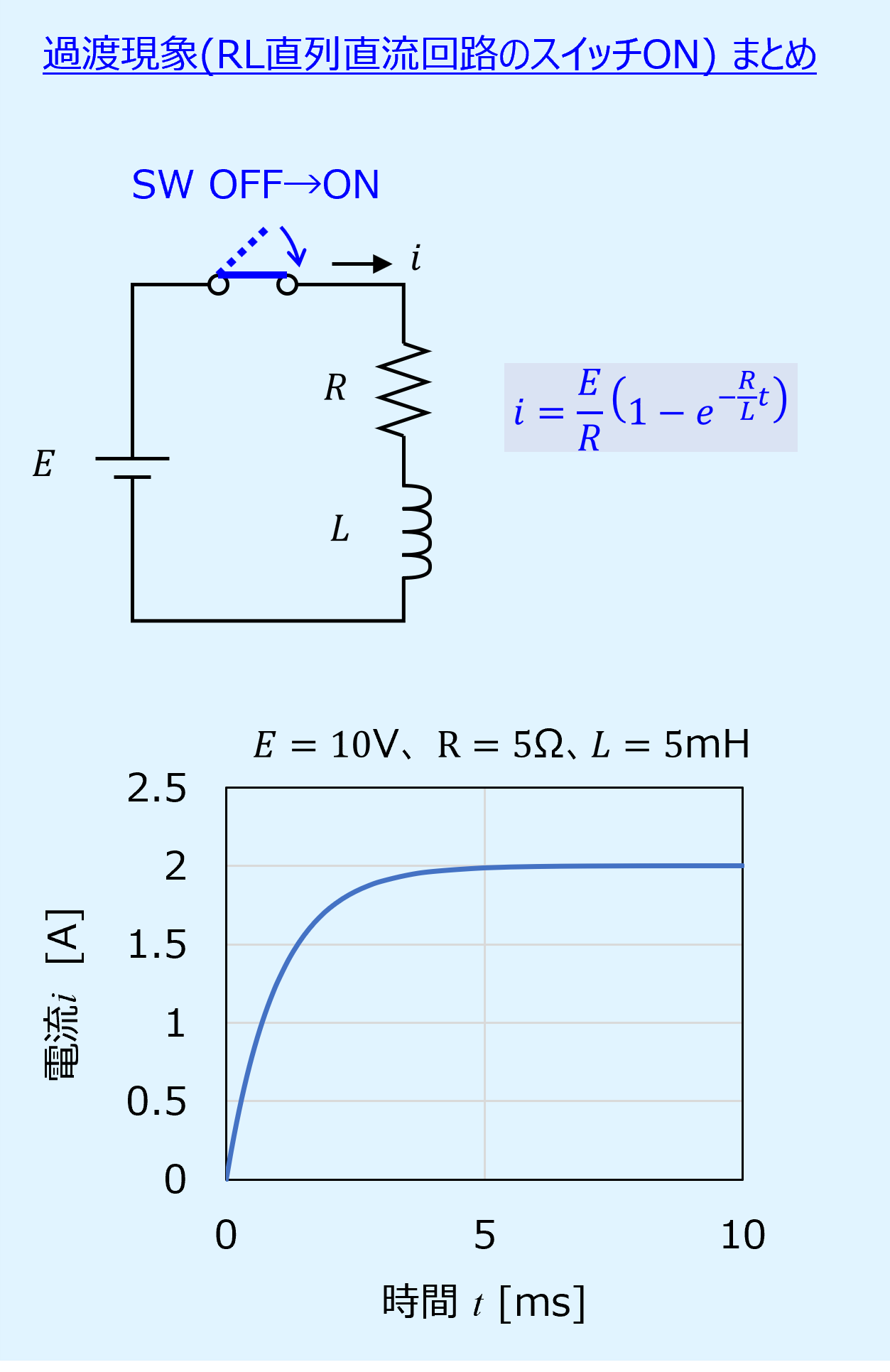
【まとめ】
本記事で取り扱う回路は、以下に示すRL直列回路に直流電源を接続したものになります。
\(E\)は電源電圧[V]、\(i\)は電流[A]、\(R\)は抵抗値[Ω]、\(L\)はインダクタンス[H]を表しています。
電源と負荷R,Lの間にあるスイッチSWをOFFからONにした時の、過渡電流がどうなるのかついて、以降で説明していきます。
電流の式導出
キルヒホッフの第2法則(電圧則)より、式(1)が得られます。
式(1)を微分すると以下となります。
次に、この微分方程式を解いて電流\(i\)を求めていきます。
電流\(i\)を以下の式(3)のように仮定します。
ここで、\(A\)、\(B\)は未定定数です。
また式(3)の1階微分、2階微分は式(4)、(5)となります。
この未定定数\(A\)、\(B\)を次に求めていきます。
式(4)、(5)を式(2)に代入すると、以下の式(6)のように、\(B\)に関する2次方程式が得られます。
2次方程式の解の公式を用いると、\(B\)は以下の式(7)となります。
式(7)で表される\(B\)を式(3)に適用すると、式(8)となります。
ここで、\(A_1\)、\(A_2\)は未定定数です。
次に、初期条件、定常条件より未定となっている\(A_1\)、\(A_2\)を求めます。
初期条件は\(t=0\)のとき、\(i=0\)なので、これを式(8)に適用すると、以下の式(9)が得られ、\(A_2\)が求まります。
式(9)を式(8)に適用すると以下の式(10)が得られます。
次に定常条件ですが、これは、\(t=\inf\)のとき\(i=E/R\)となります。
これを式(10)に適用すると、以下の式(11)が得られ、\(A_1\)が求まります。
式(11)を式(10)に適用すると、電流\(i\)の式として、最終的に式(12)が得られます。
過渡現象における電圧
RL直列回路のスイッチをONにしたときの抵抗の電圧は次式で表されます。
またインダクタの電圧は次式で表されます。
その他
電気回路全般については以下をご覧下さい。
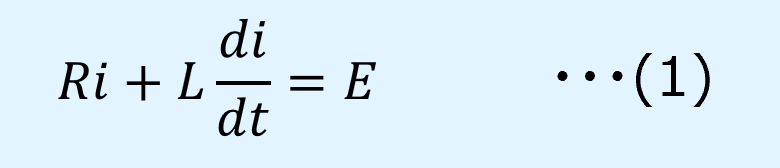
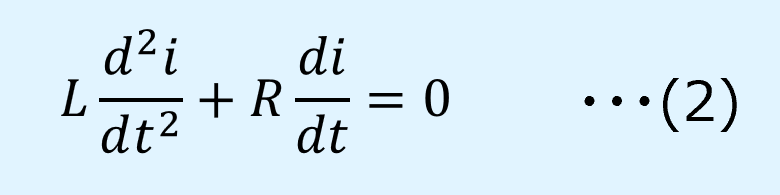
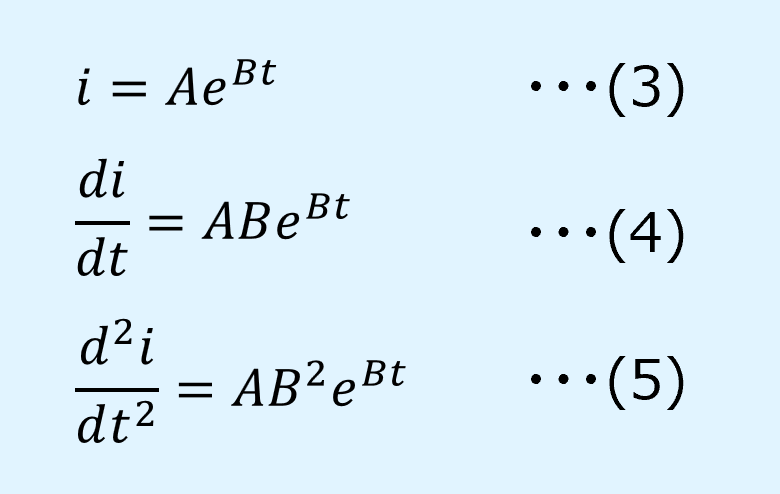
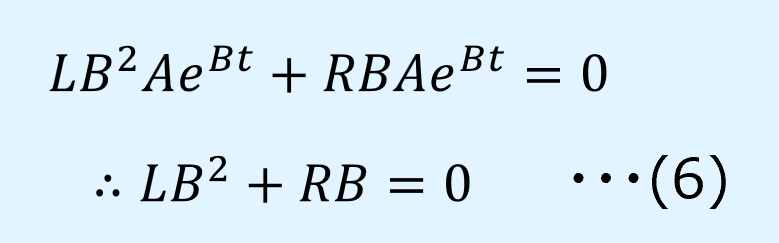
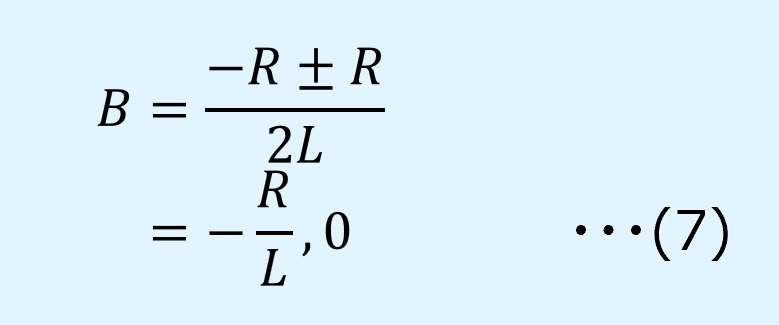
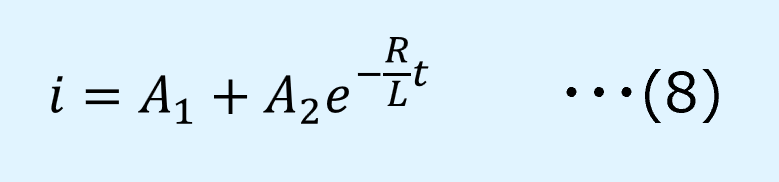

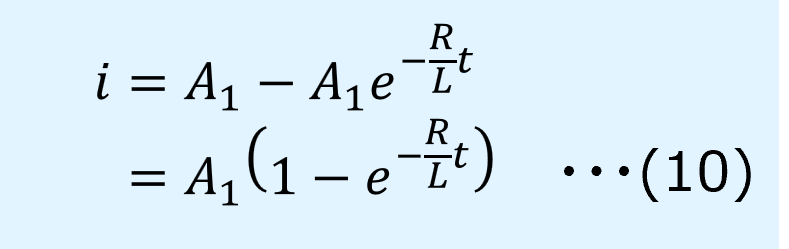

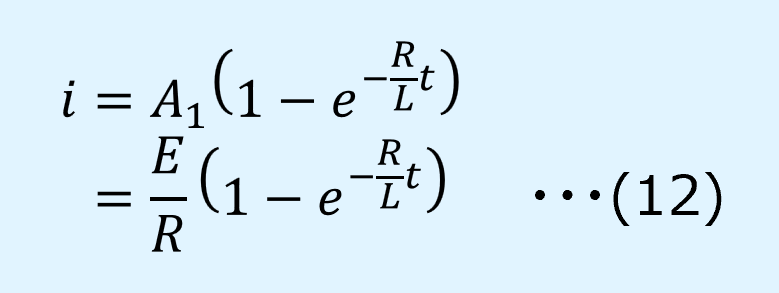
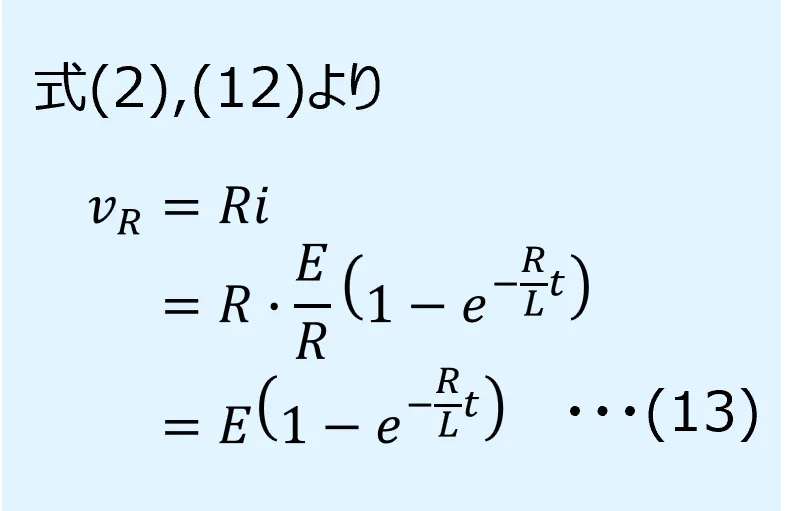

コメント