この記事では電気回路や信号処理で生じる波形の合成について、一般化した場合について説明をします。
別の記事で振幅と位相が異なる場合、周波数が異なる場合での波形合成について説明しましたが、本記事はその両者を組み合わせた場合となります。
目次
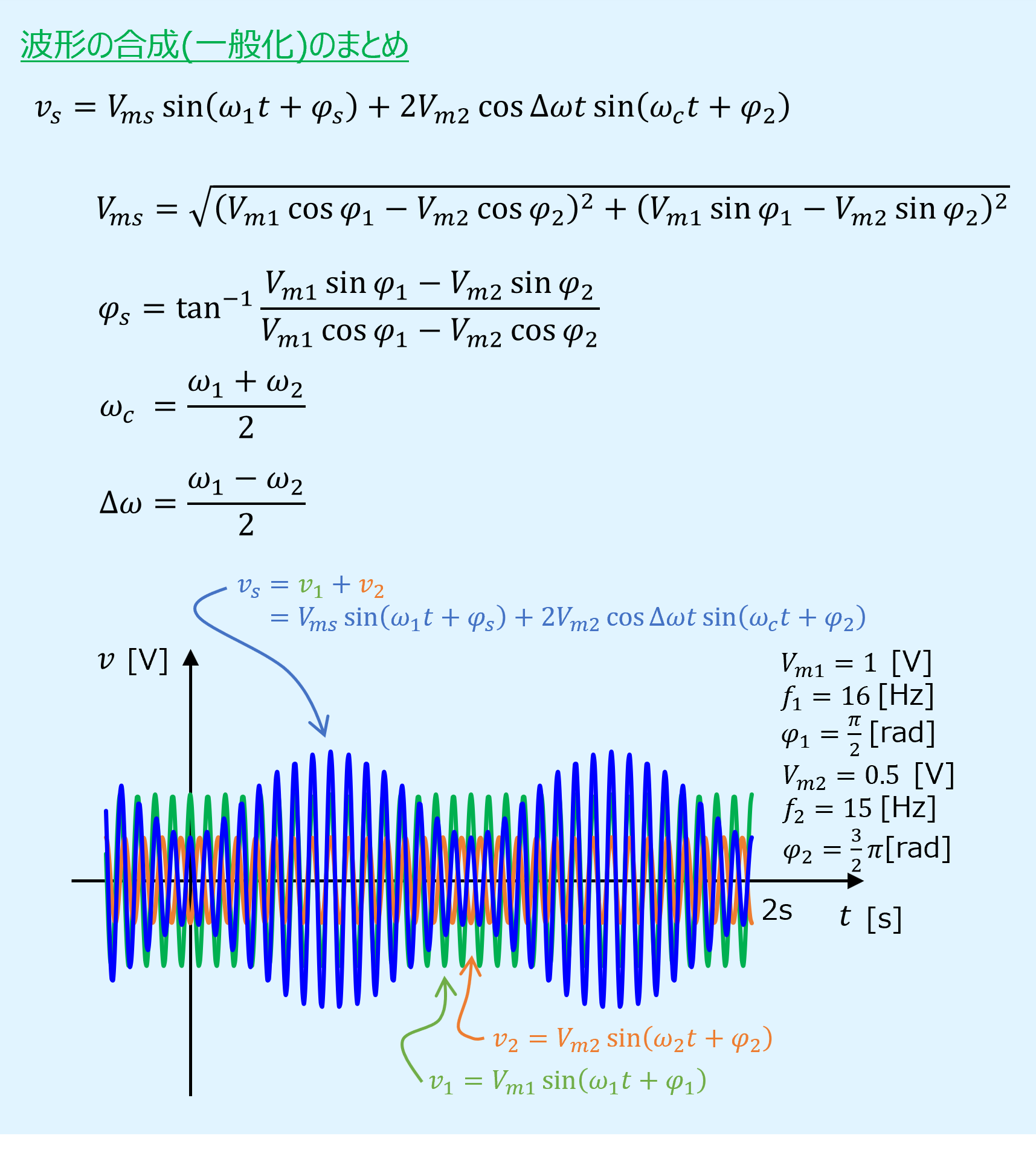
【まとめ】波形の合成(一般化)
最初にまとめです。
一般化した波形の合成式
一般化した波形の合成では、合成元である2つ正弦波の振幅、周波数、位相が異なることになります。
振幅\(V_{m1}\)、\(V_{m2}\)、角周波数\(\omega_1\)、\(\omega_2\)、位相\(\varphi_1\)、\(\varphi_2\)とすると正弦波\(v_1\)、\(v_2\)は以下の式となります。
上記の2式を合成すると以下となります。
これ以上の式変形をこのまま続けるのは難しいため、波形を観察してその特徴から中間式の仮定を行い、最後に中間式から一般化した式の導出を行います。
波形の観察と中間式の仮定
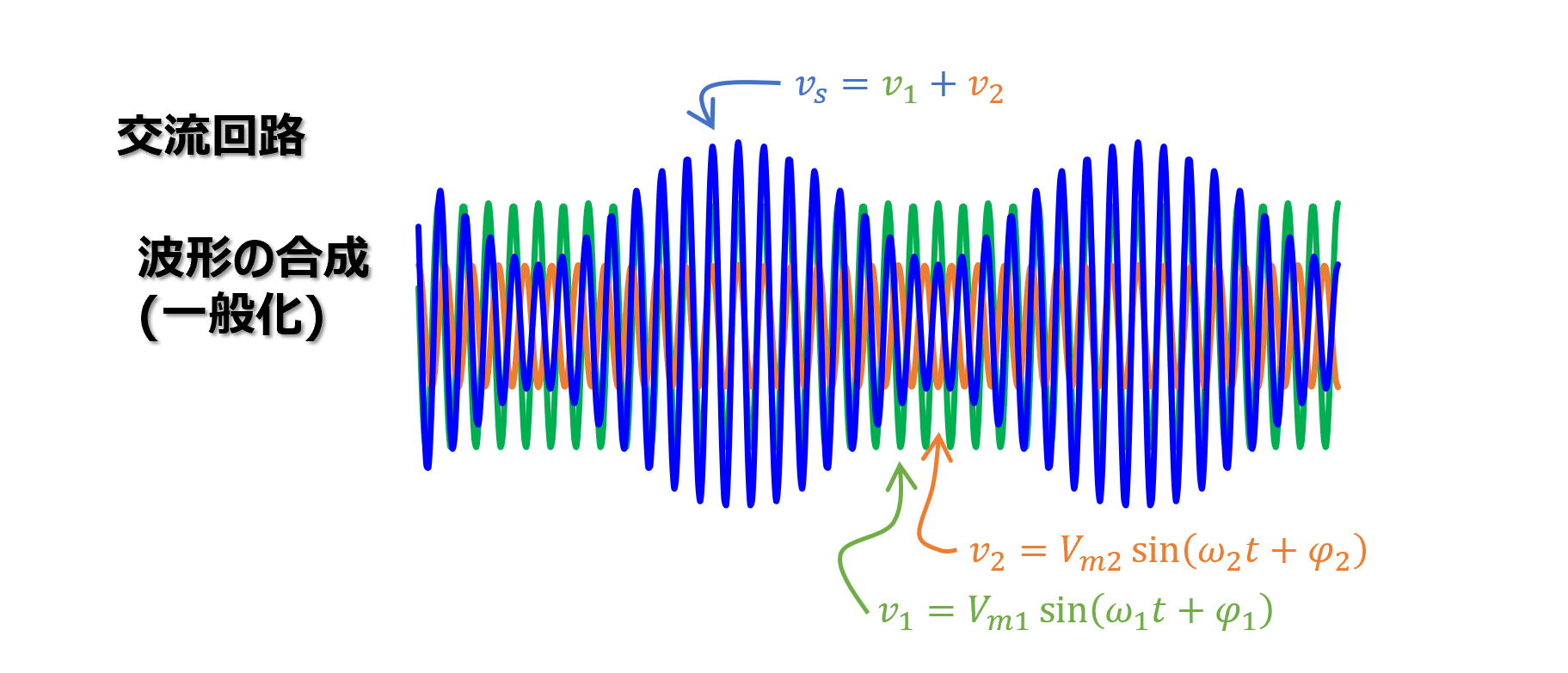
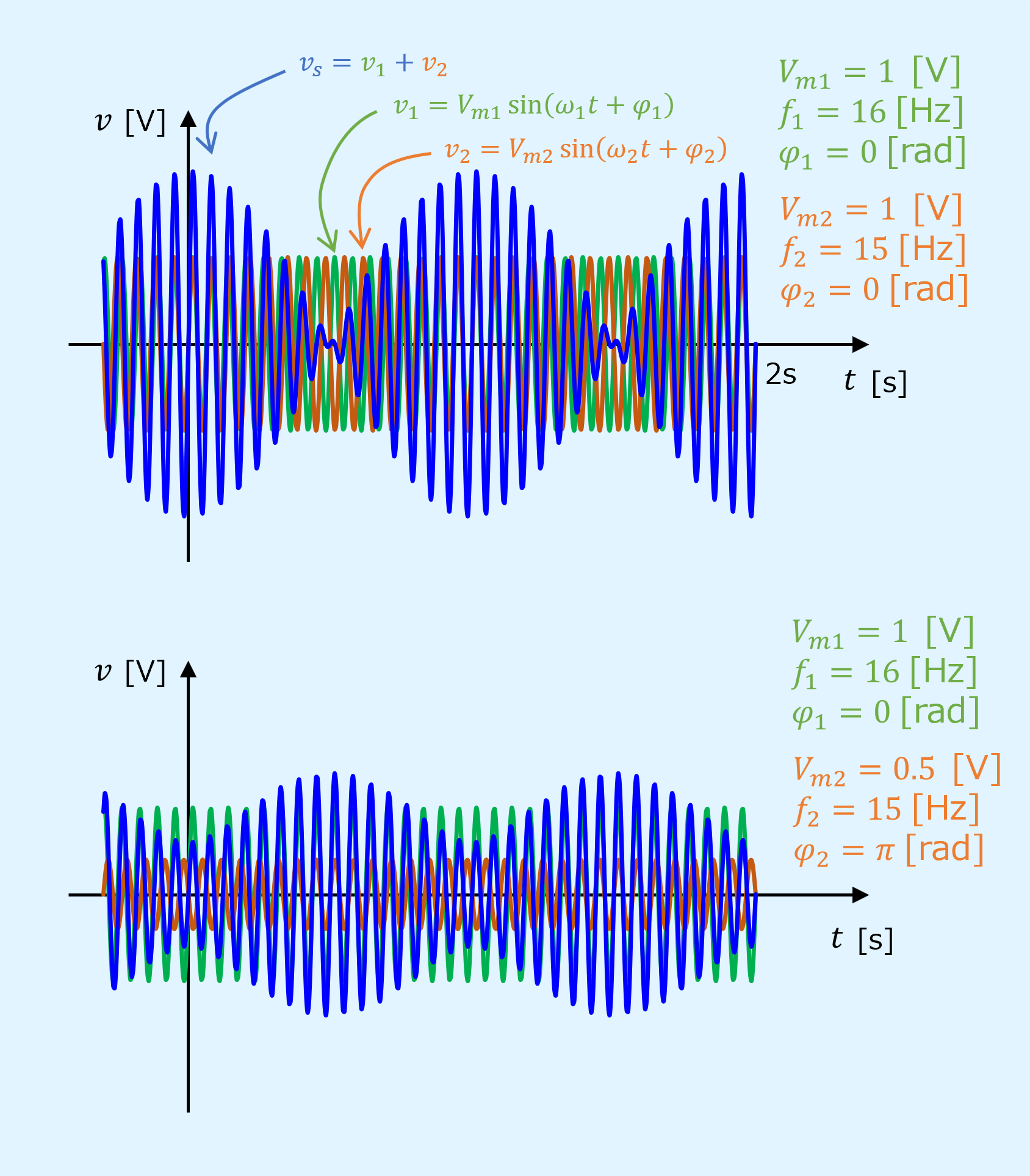
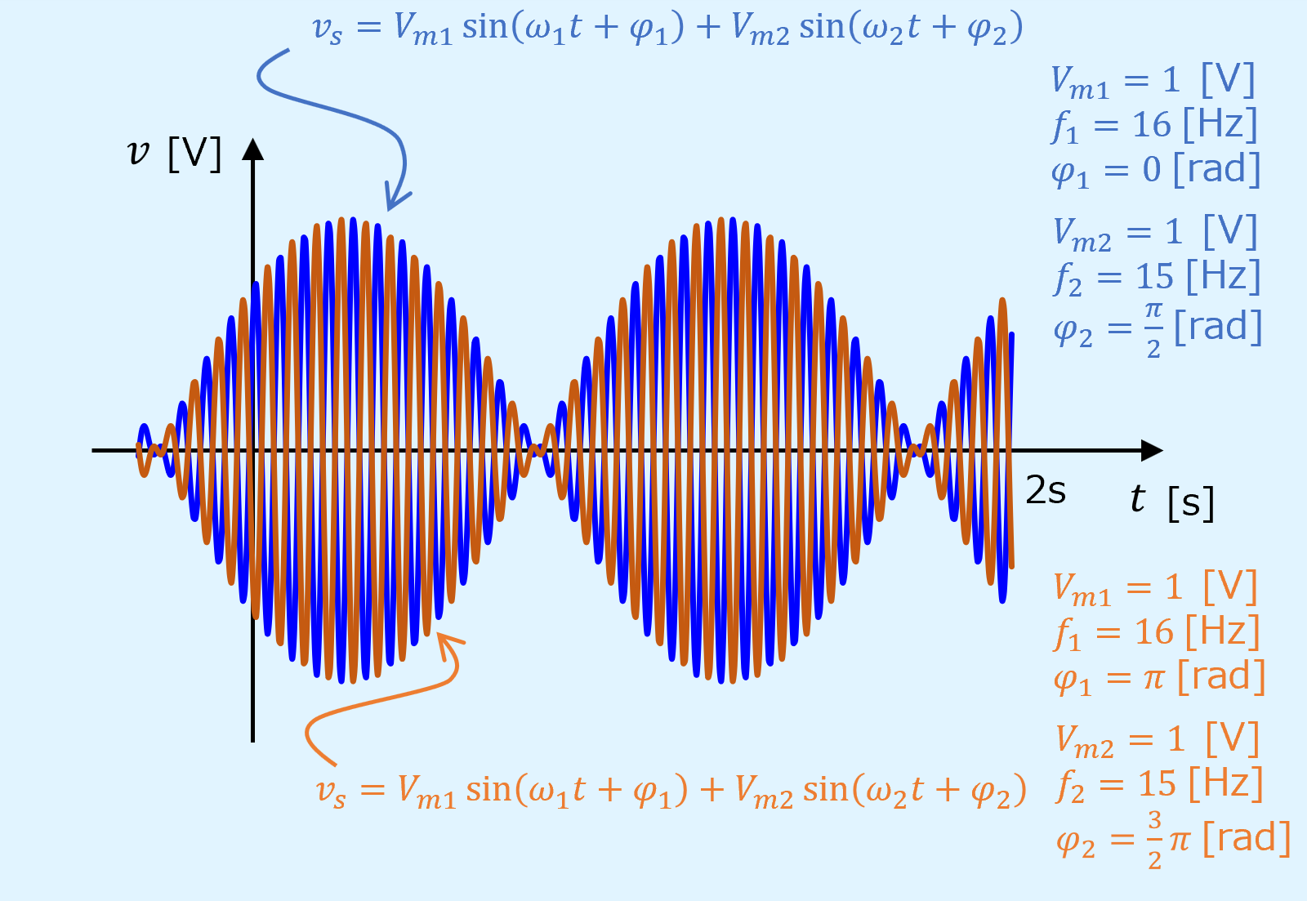
以下の図は上段と下段で振幅と位相を変えたものですが、これから以下のことがいえます。
- 振幅は\(V_{m1}\)を中心として\(V_{m1}-V_{m2}\)の範囲で変動する
- うなりの位相は2つの波形の位相差\(\varphi_1-\varphi_2\)にみに依存する
- うなりの周期は2つの波形の周波数差\(f_1-f_2\)の逆数である
以上から、以下のように式の仮定を一度行います。
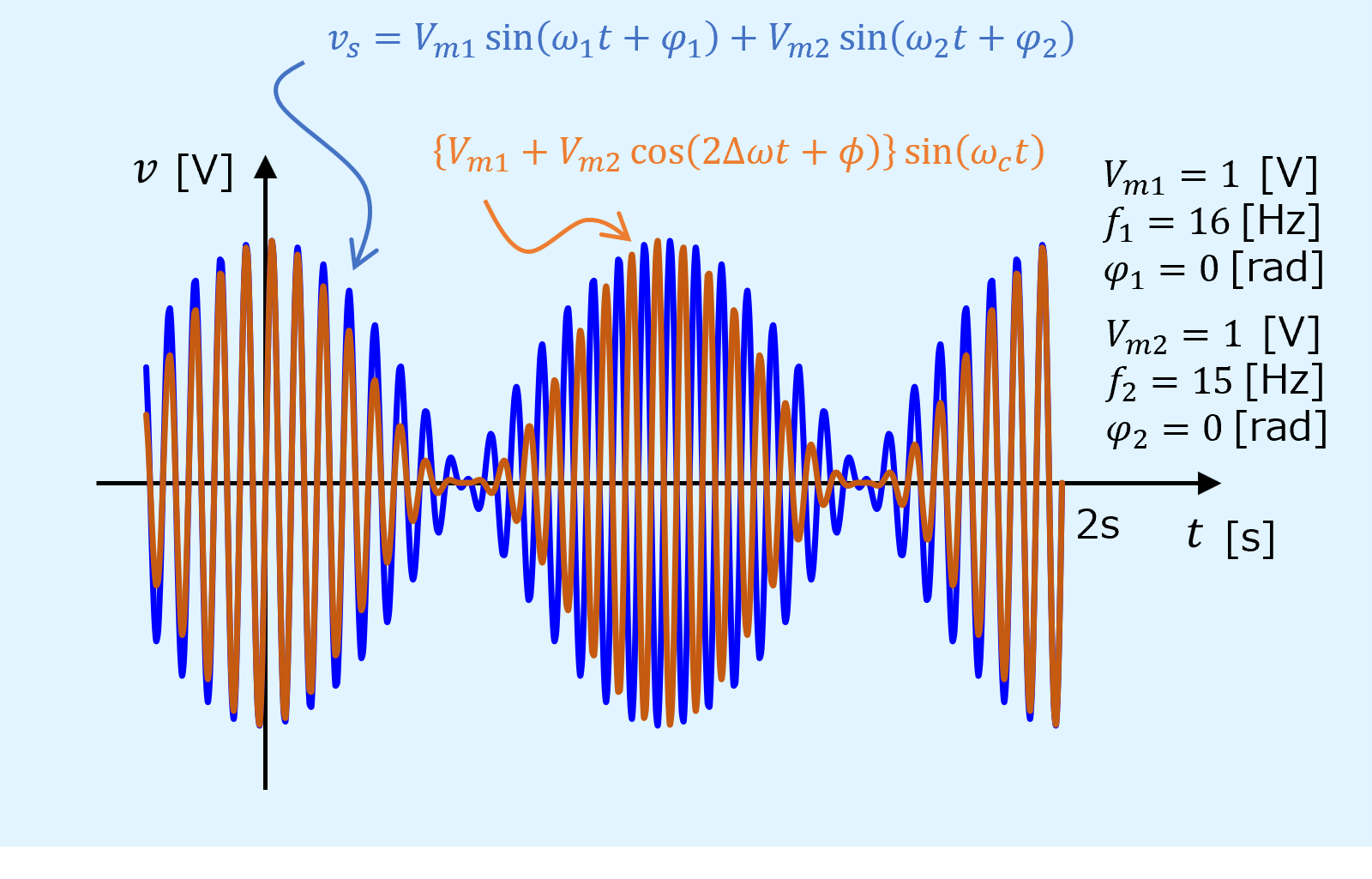
下図のように上記の仮定式の波形と2つの波形の合成波形を比較すると次のことが分かります。
- 正弦波の周波数は2つの波形の中心周波数\(\omega_c\)ではなく、\(\omega_1\)である。
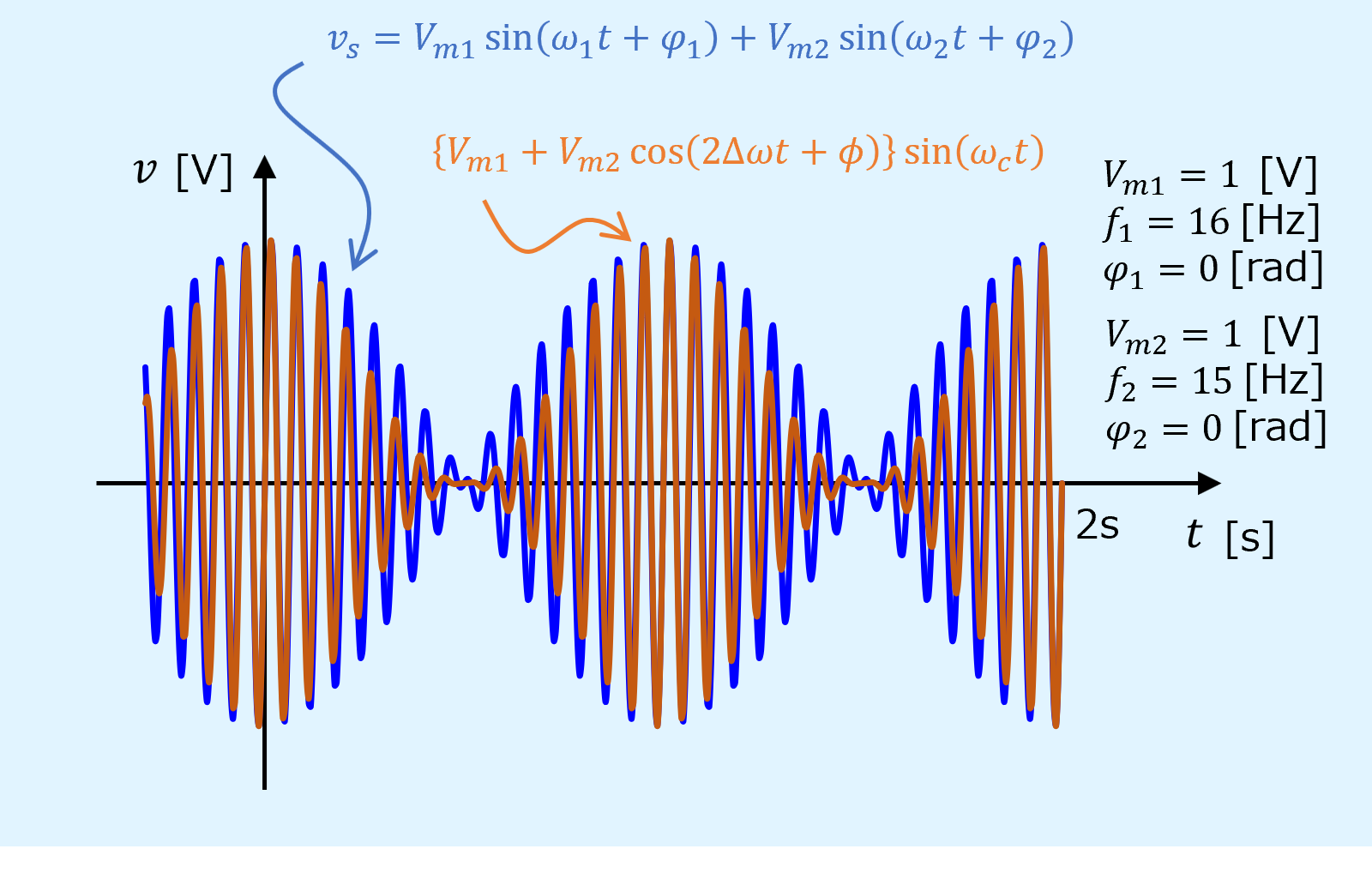
以上から式を以下のように仮定し直し、図示すると、2つの波形の合成波に近づいていることが分かる。
また、下図のように2つの波形の位相差を保ったまま位相を変化させると以下が分かる。
- 正弦波の位相は\(\varphi_1\)である。
以上の波形観察より、中間式は以下となる。
ここで後付けとなるが、第2項を追加して波形の大きさを合わせている。
中間式が2つの波形の合成であることの証明
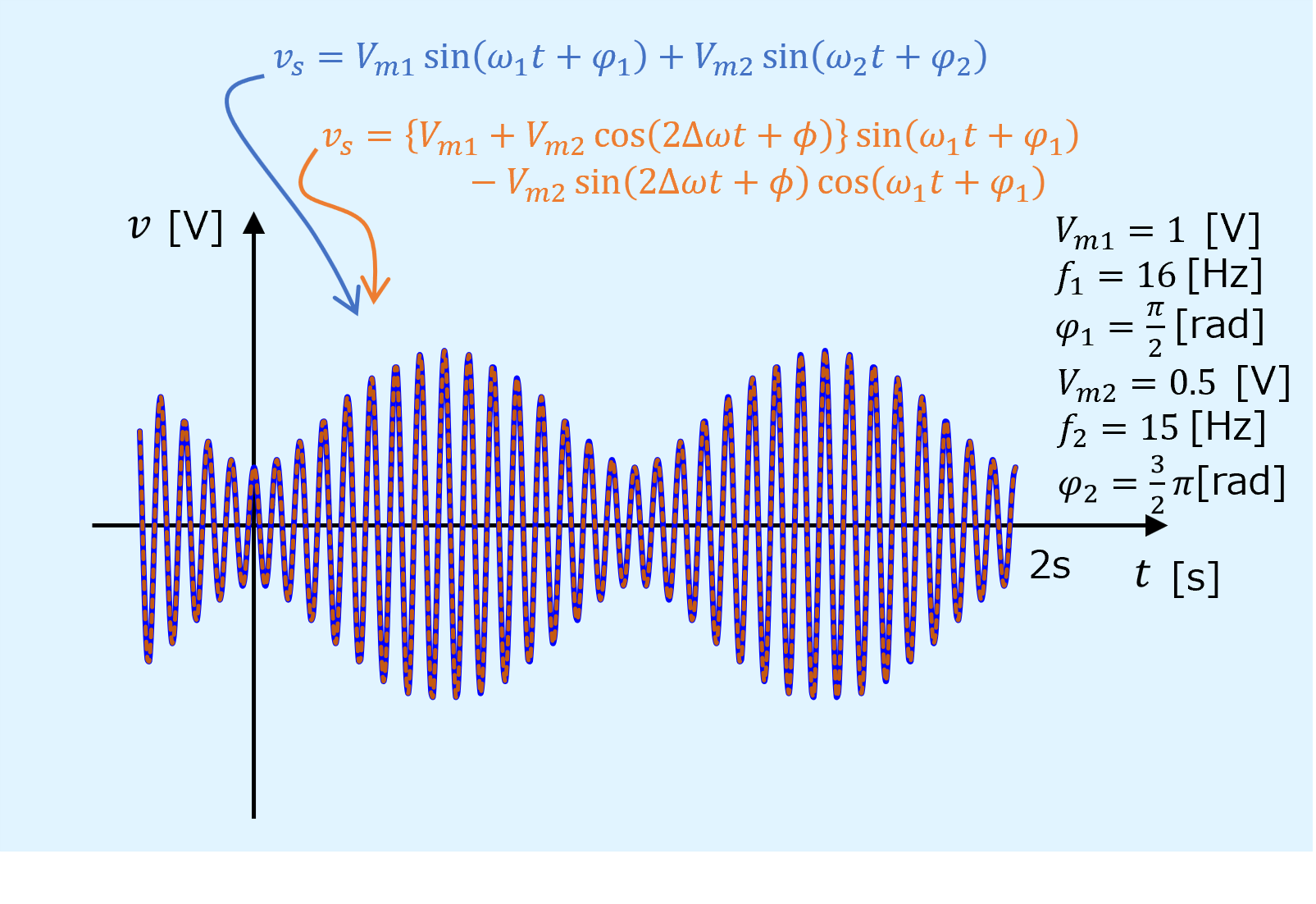
この中間式が2つの波形の合成であることは実際に図示してみると分かります。
また、以下のように式変形をしていくと同じであることが分かります。
中間式から一般化した式の導出
中間式から式変形を行い、一般化した式にすると、以下となります。
式変形の仮定は以下となります。
一般化した式であることの証明例
最後に一般化した式であることの証明として、別の記事で紹介した、周波数が2つとも同じ場合と振幅が1、位相が0の場合と同じ式になることを示します。
周波数が2つとも同じ場合は\(\omega_1=\omega_2=\omega\)とおくと、以下のように式変形ができます。
振幅が1の場合は\(V_{m1}=V_{m2}=1\)、位相が0の場合は\(\varphi_1=\varphi_2=0\)とおくと、以下のように式変形ができます。
以上より、本記事で紹介した式が一般化された式であることが確認できます。
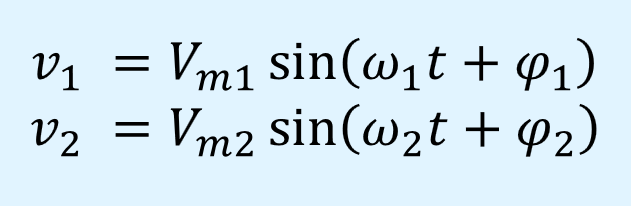
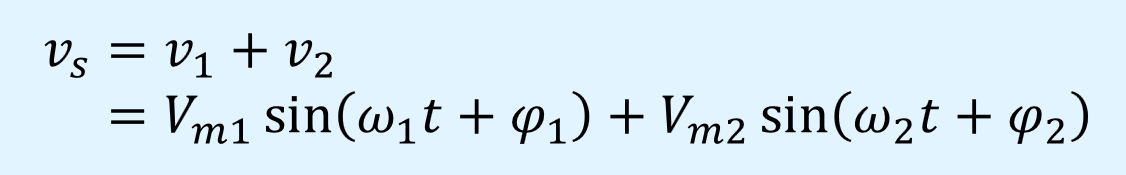
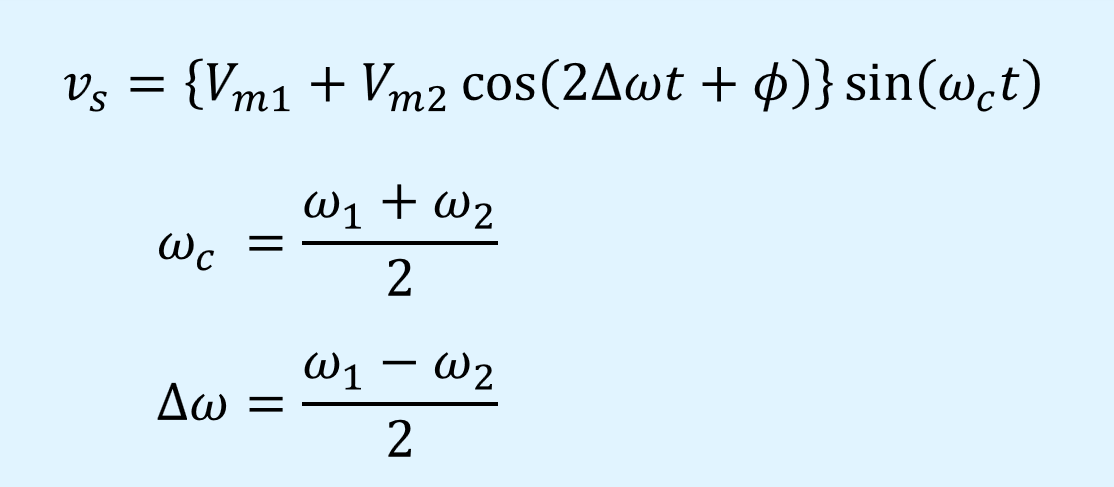
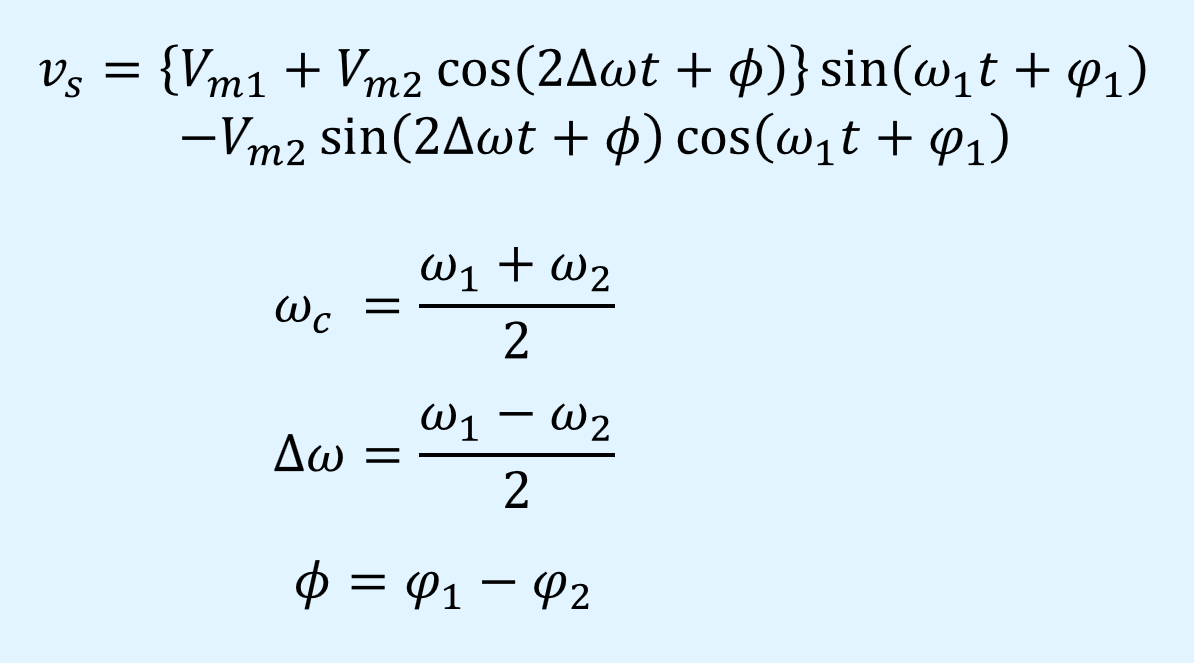

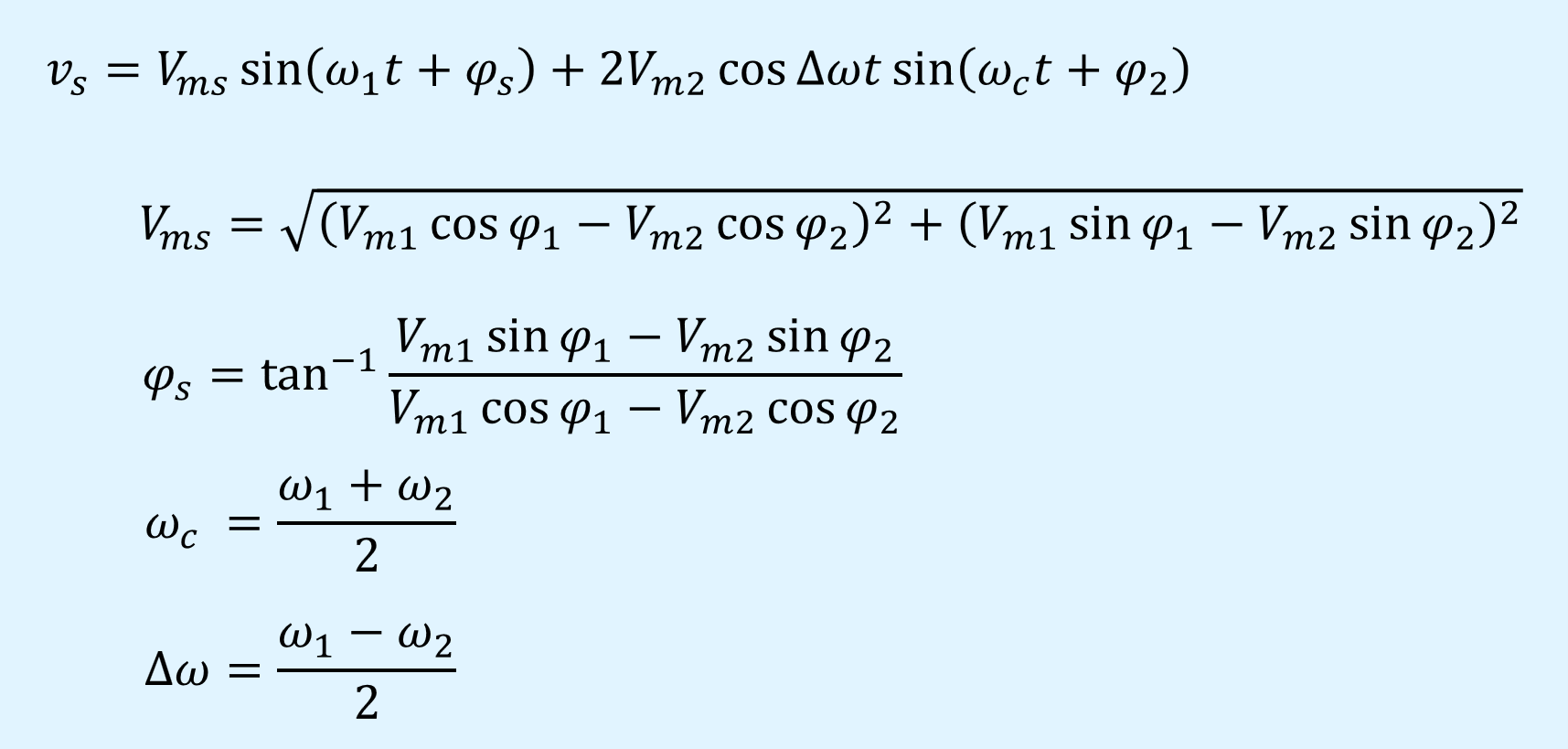
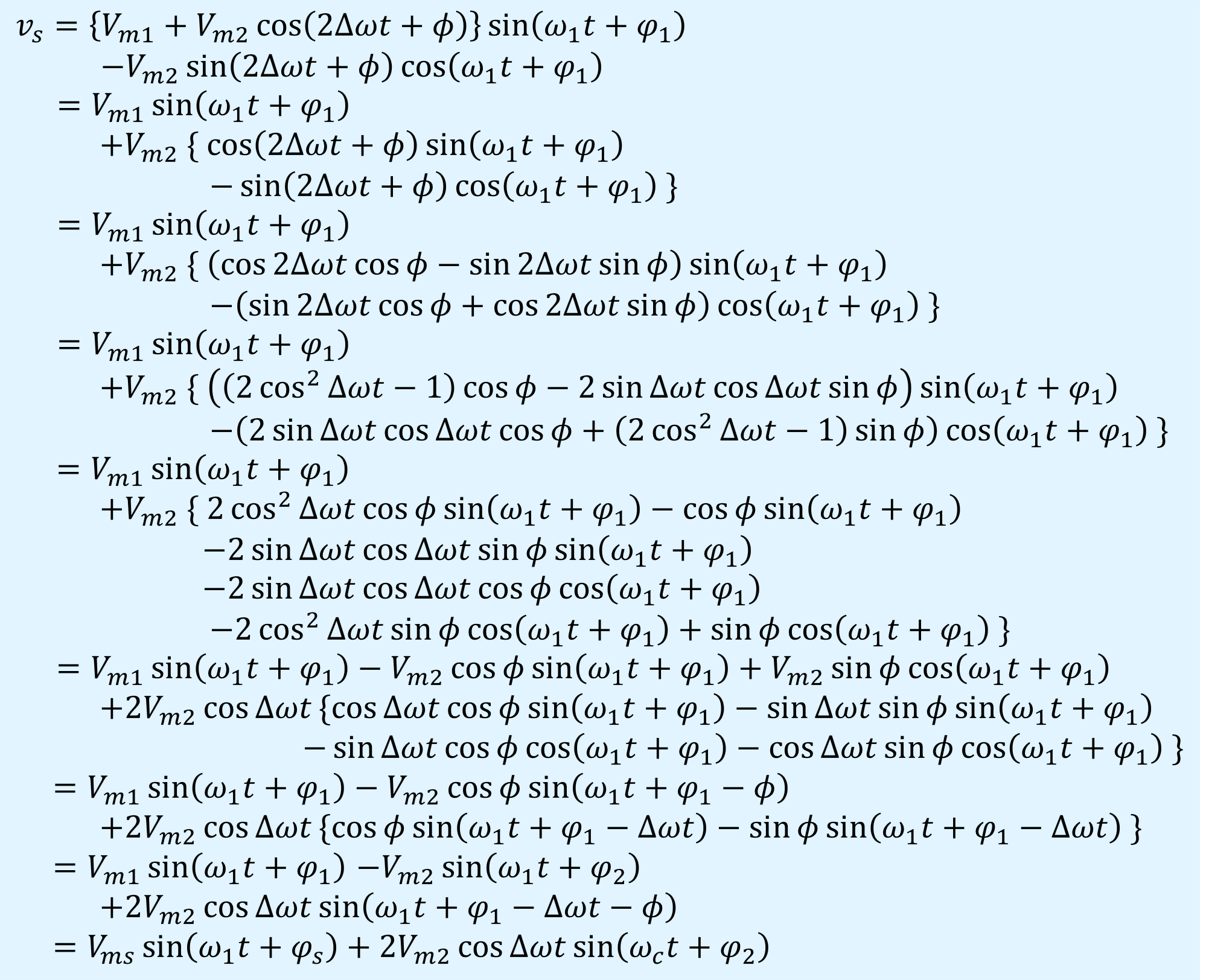
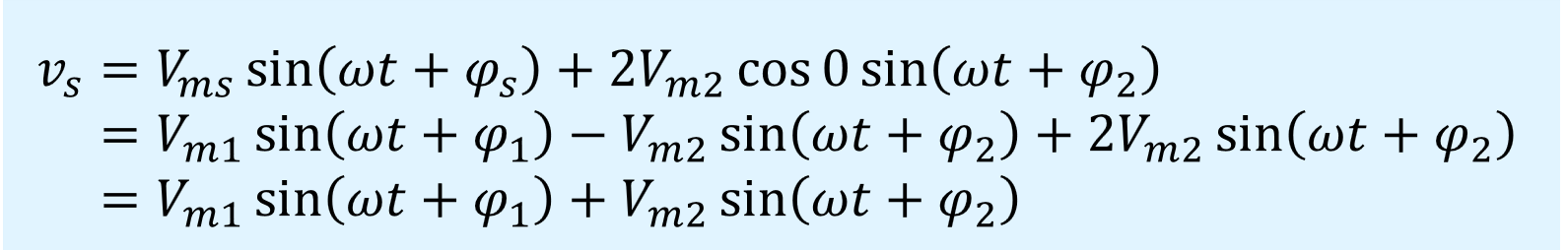
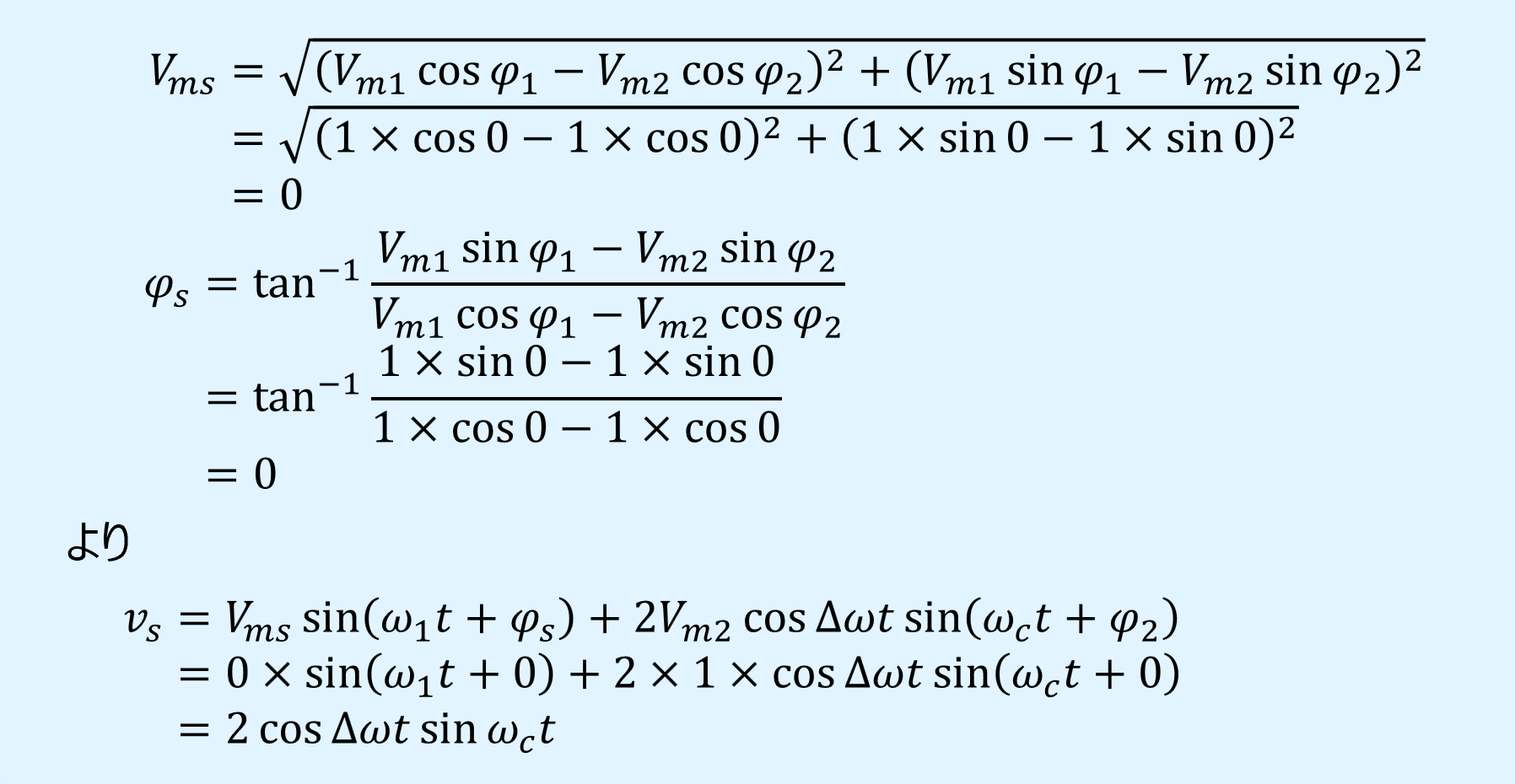


コメント