この記事では数学や情報処理で用いられる集合の性質について説明をします。
相等関係、部分集合の性質、空集合と任意の集合のとの関係を取り扱います。
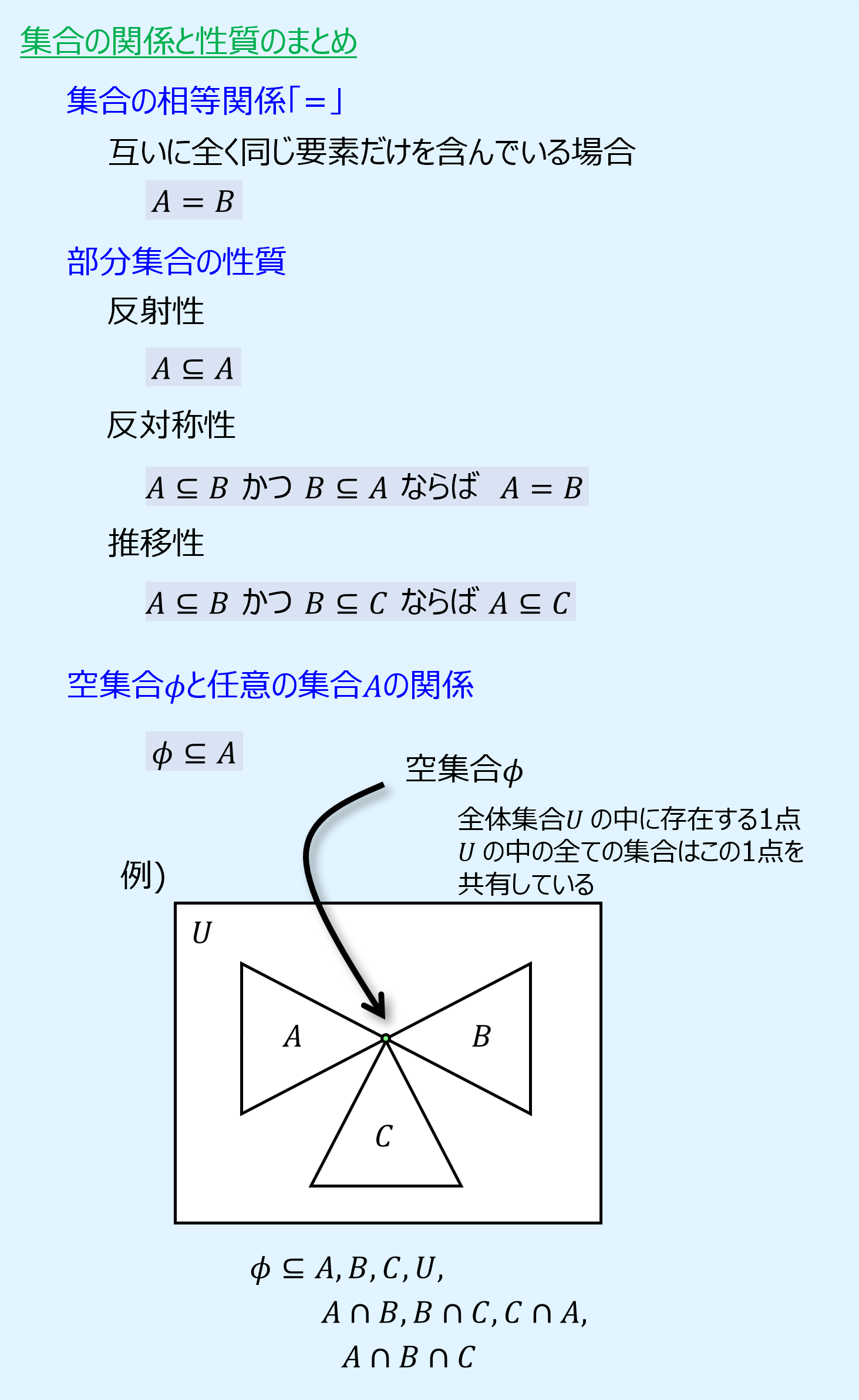
【まとめ】集合の関係と性質
最初にまとめです。
集合の相等関係「=」
集合\(A\) が、集合\(B\) に含まれている要素と全く同じ要素だけを含んでいるのならば、2つの集合\(A\) と \(B\)は等しいといい、
\(A=B\)
と書きます。
部分集合の性質
部分集合を表す包含関係「\(\subseteq\)」は、定義から次の3つの性質を持っています。
反対称性を利用すると、「2つの集合が等しいことの証明」を、「\(A{\subseteq}B\)かつ\(B{\subseteq}A\)であることの証明」に置き換えられることができます。
空集合と任意の集合との関係
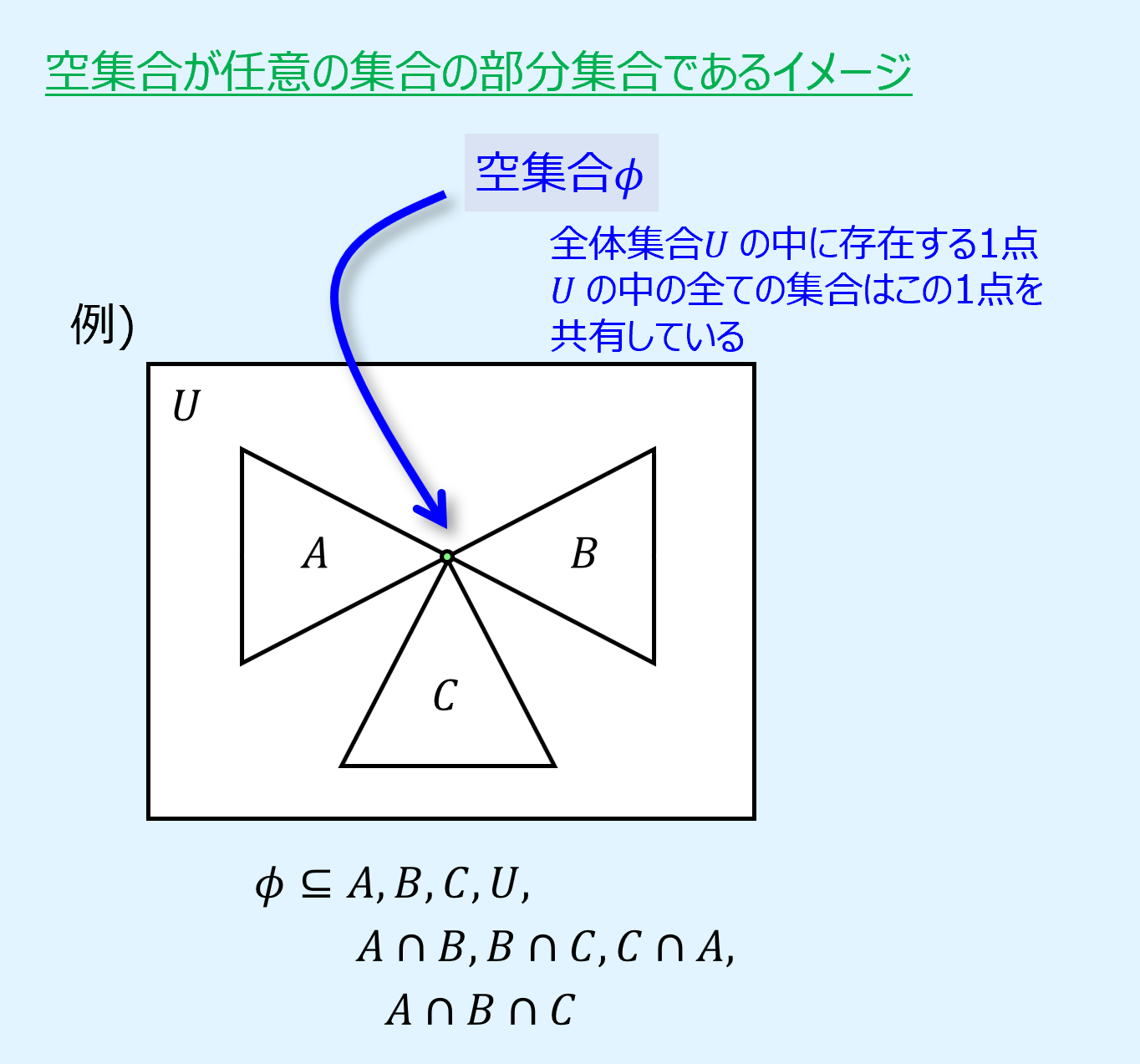
空集合\(\phi=\{ \}\)は任意の集合\(A\)の部分集合であり、以下のように表せます。
\(\phi{\subseteq}A\)
証明方法はいくつかありますが、ここでは説明として以下にイメージを示します。
その他
集合演算と論理演算全般については以下をご覧下さい。





コメント