この記事では数学や情報処理で用いられる集合の種類について説明をします。
情報処理で操作を行う際に対象がどのような集合であるのか等の、定義に用いられますのでしっかり覚えましょう。
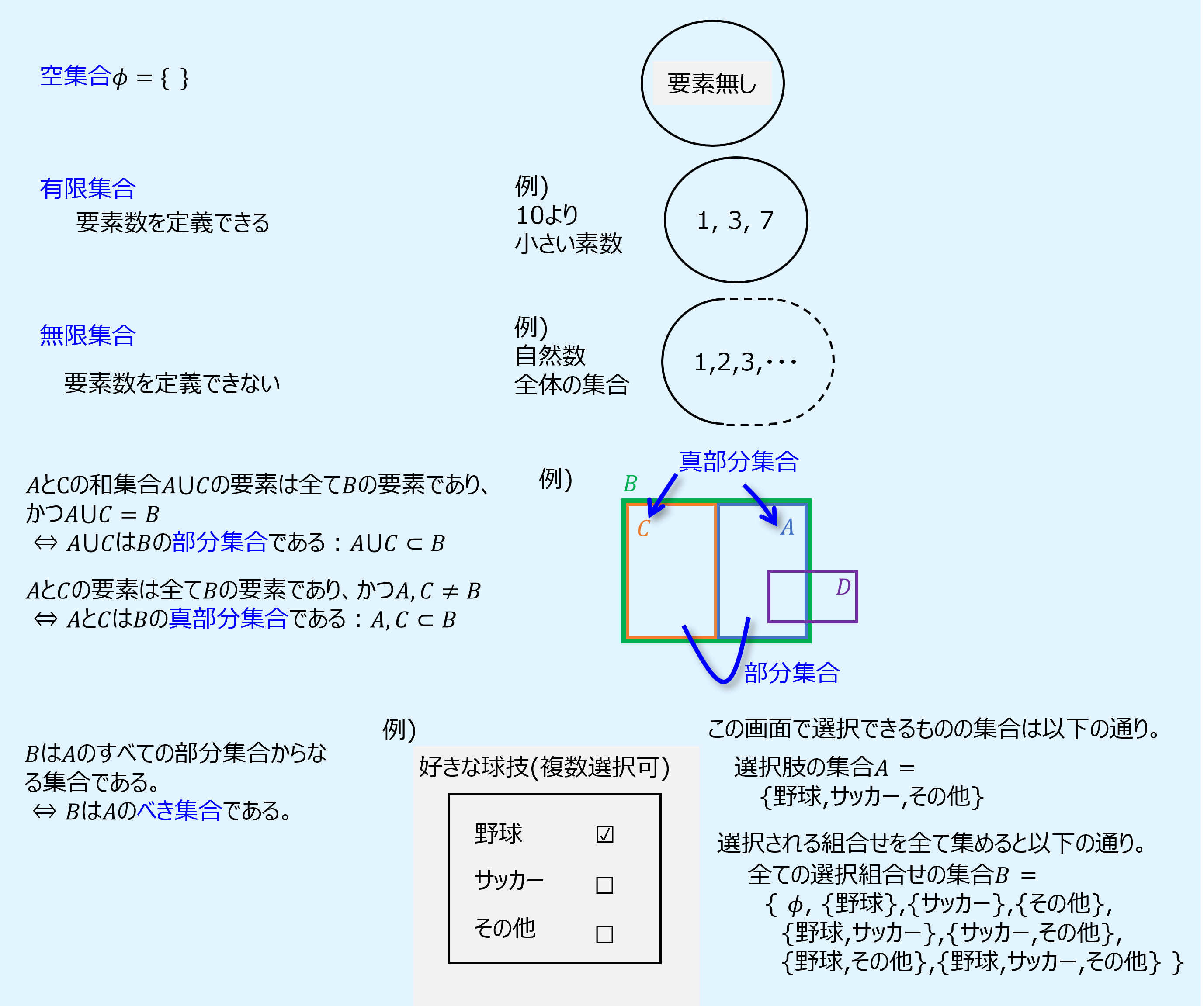
【まとめ】集合の種類
最初にまとめです。
空集合
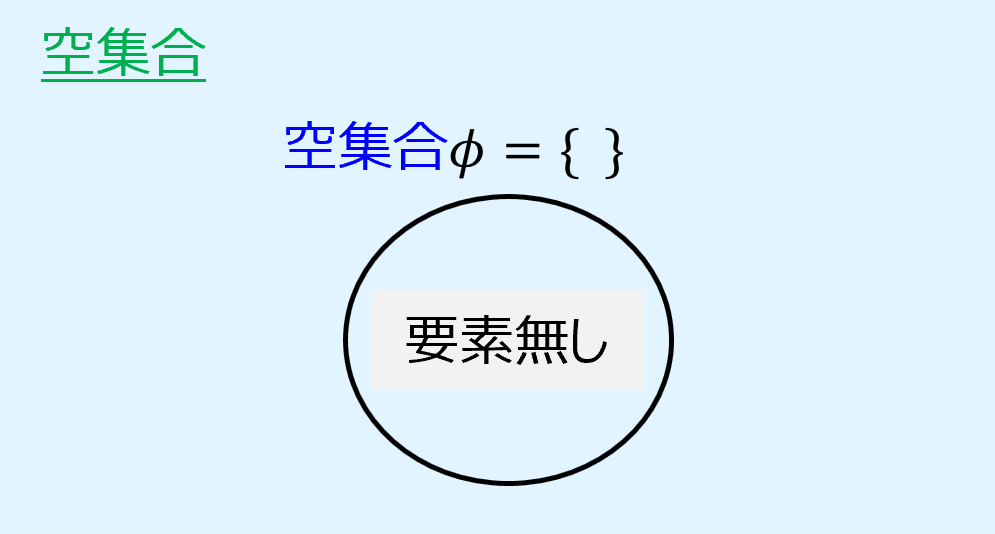
空集合(empty set)とは要素を全く含まない集合のことです。
記号では\(\phi\)で表します。
また、外延的記法では{ }と書くことができます。
空集合のイメージを以下に示します。
有限集合と無限集合
要素数が有限である集合のことを有限集合(finite set)といいます。
例えば10より小さい素数の集合だと{1,3,7}となります。
要素数が無限である集合のことは無限集合(infinite set)と言います。
例えば自然数全体の集合だと{1,2,3,…}となります。
有限集合と無限集合のイメージを以下に示します。
部分集合と真部分集合
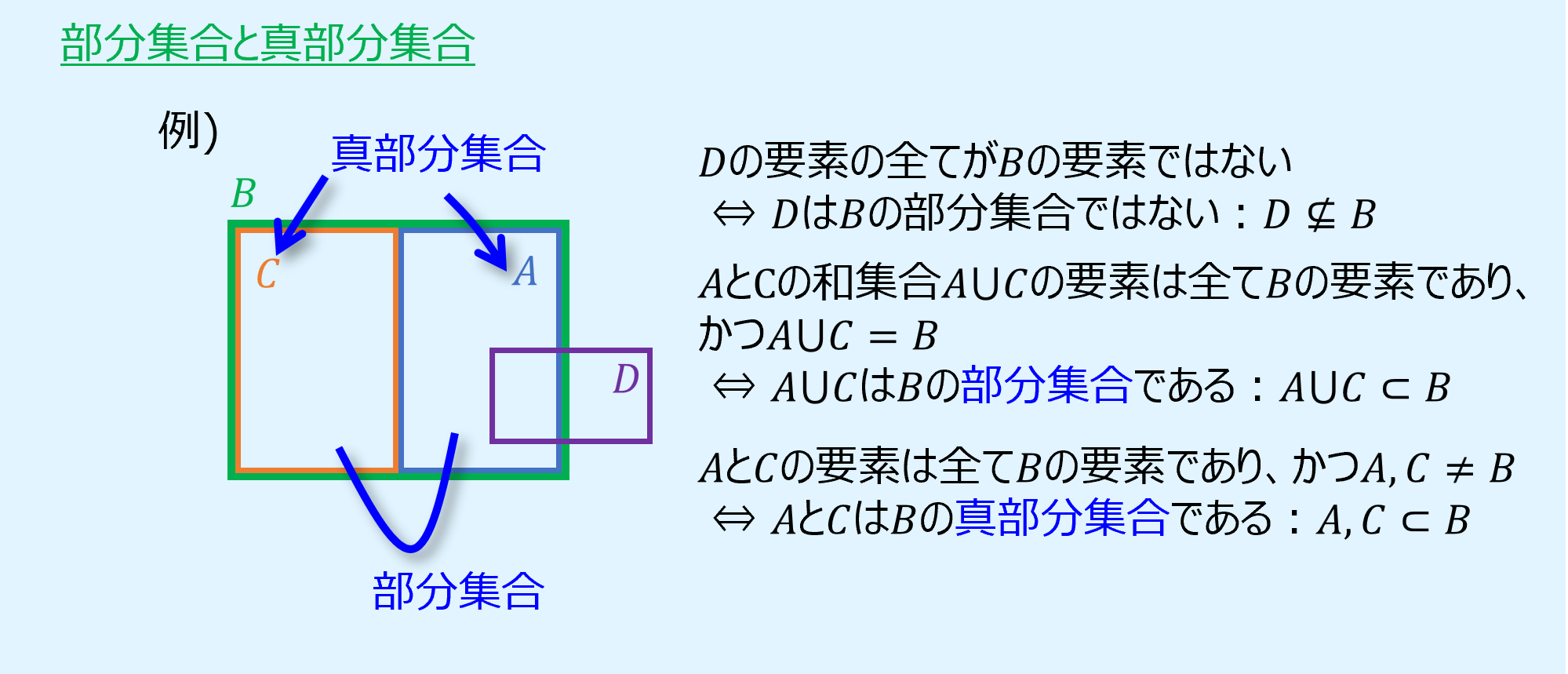
集合Aのすべての要素が集合Bの要素でもあるとき、AはBの部分集合(subset)であるといい、次のように表します。
逆に、AがBの部分集合では無い場合は次のように表します。
また、AとBが一致しないとき、すなわちA⊆BかつA≠Bであるとき、AはBの真部分集合(proper subset)といい、次のように表します。
部分集合と真部分集合のイメージを以下に示します。
べき集合
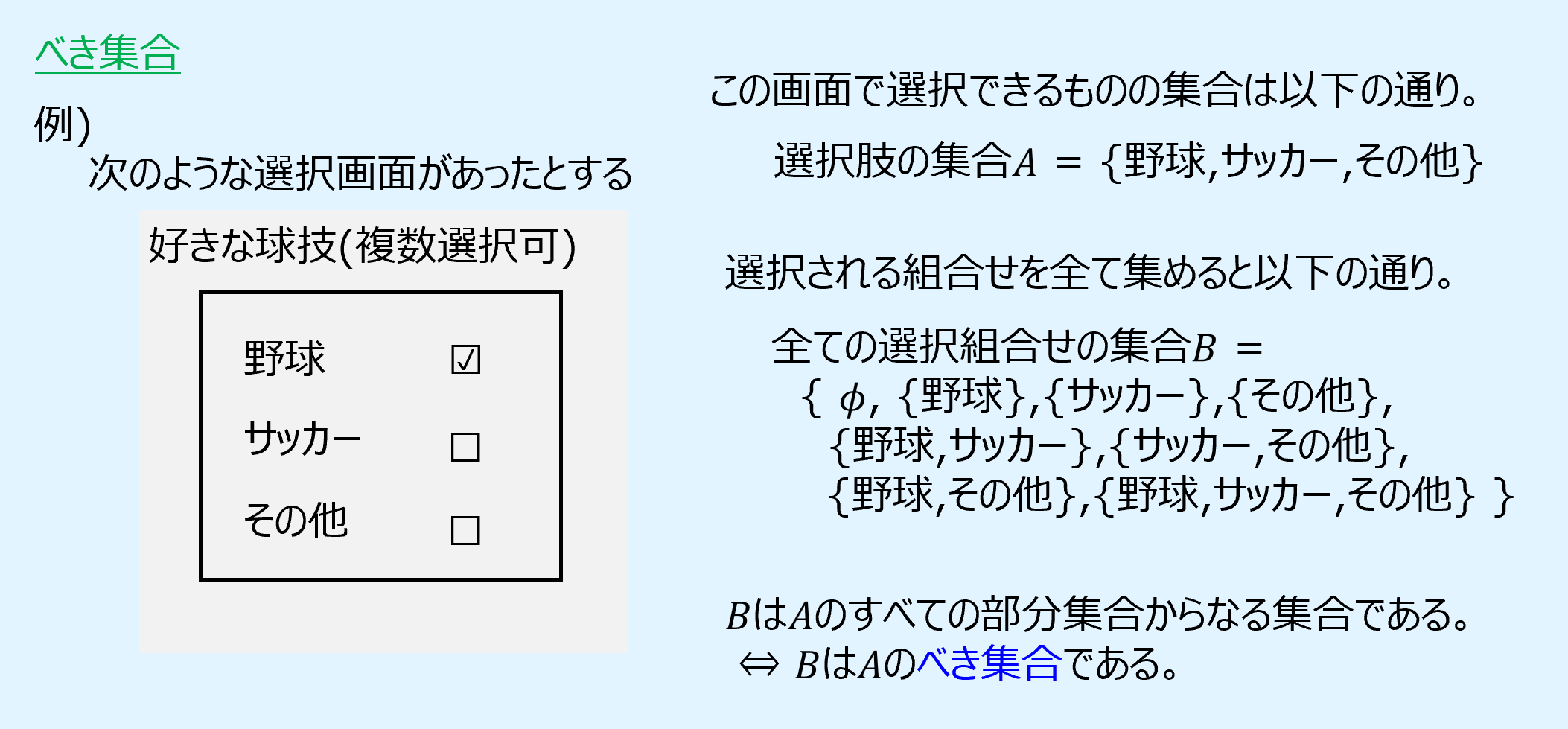
ある集合Aのすべての部分集合からなる集合のことをべき集合(power set)といいます。
べき集合をイメージを以下に示します。







コメント