交流電圧、電流

【まとめ】交流電圧、電流

交流電圧、電流とは

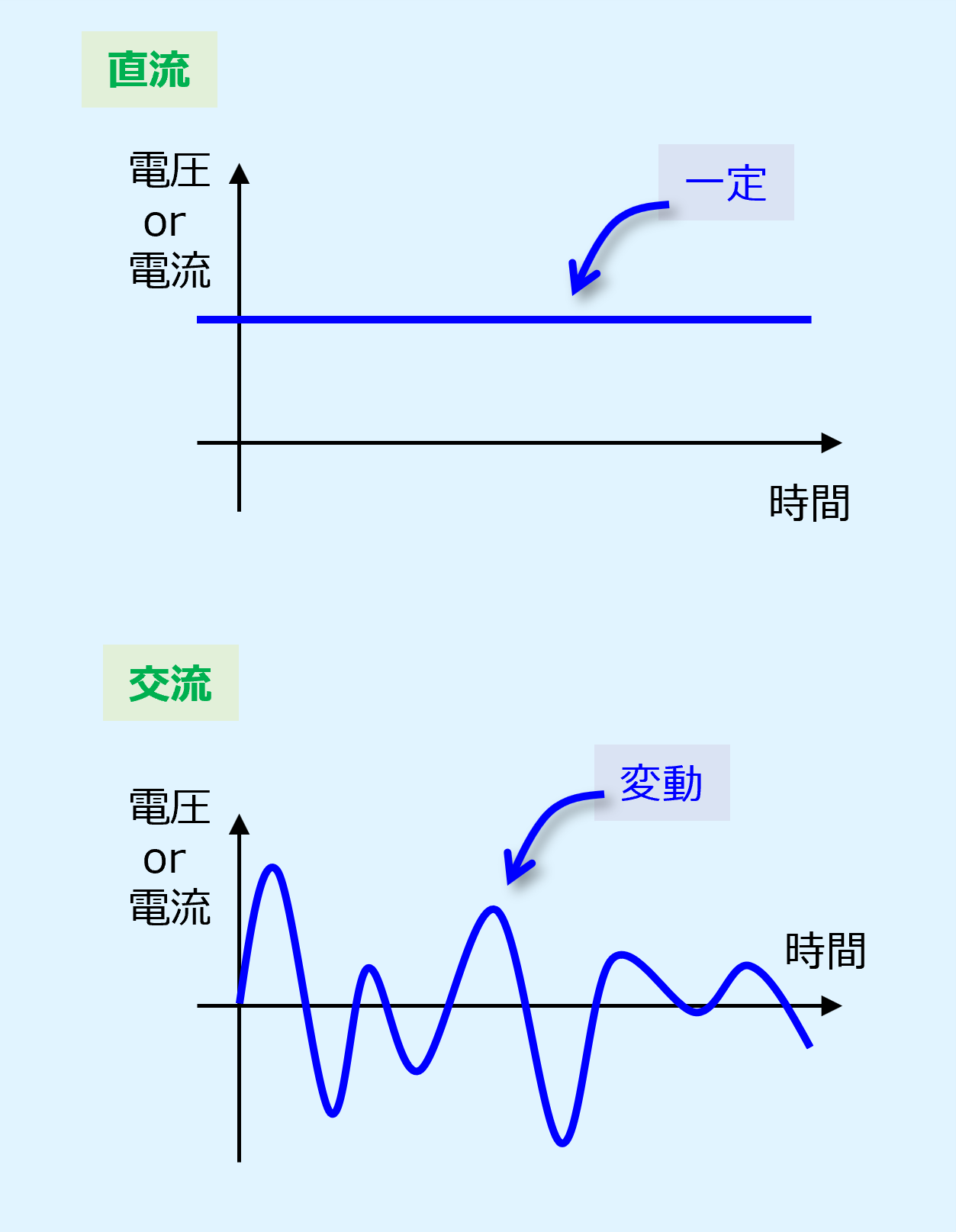
時間に対して大きさや向きが変化する電圧、電流を、交流電圧(alternating voltage)、交流電流(alternating current)といいます。

なお、実際には直流回路にも交流成分が入っていたり、交流回路にも直流成分が入っていたりするので注意しましょう。

交流波形

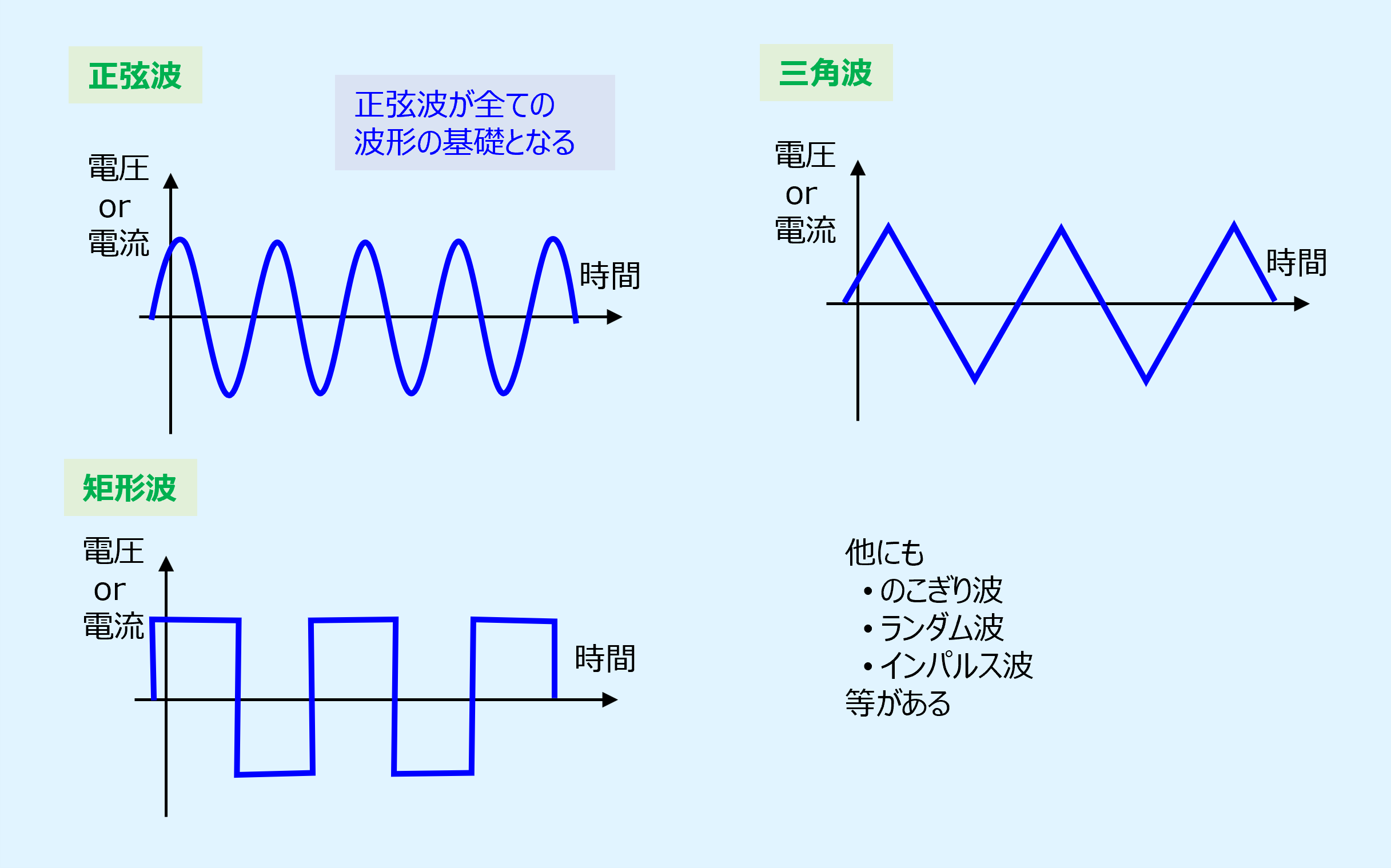
交流の波形は正弦波、矩形波、三角波等、複数あります。
以降では基本となる正弦波について説明します。

正弦波の式と波形

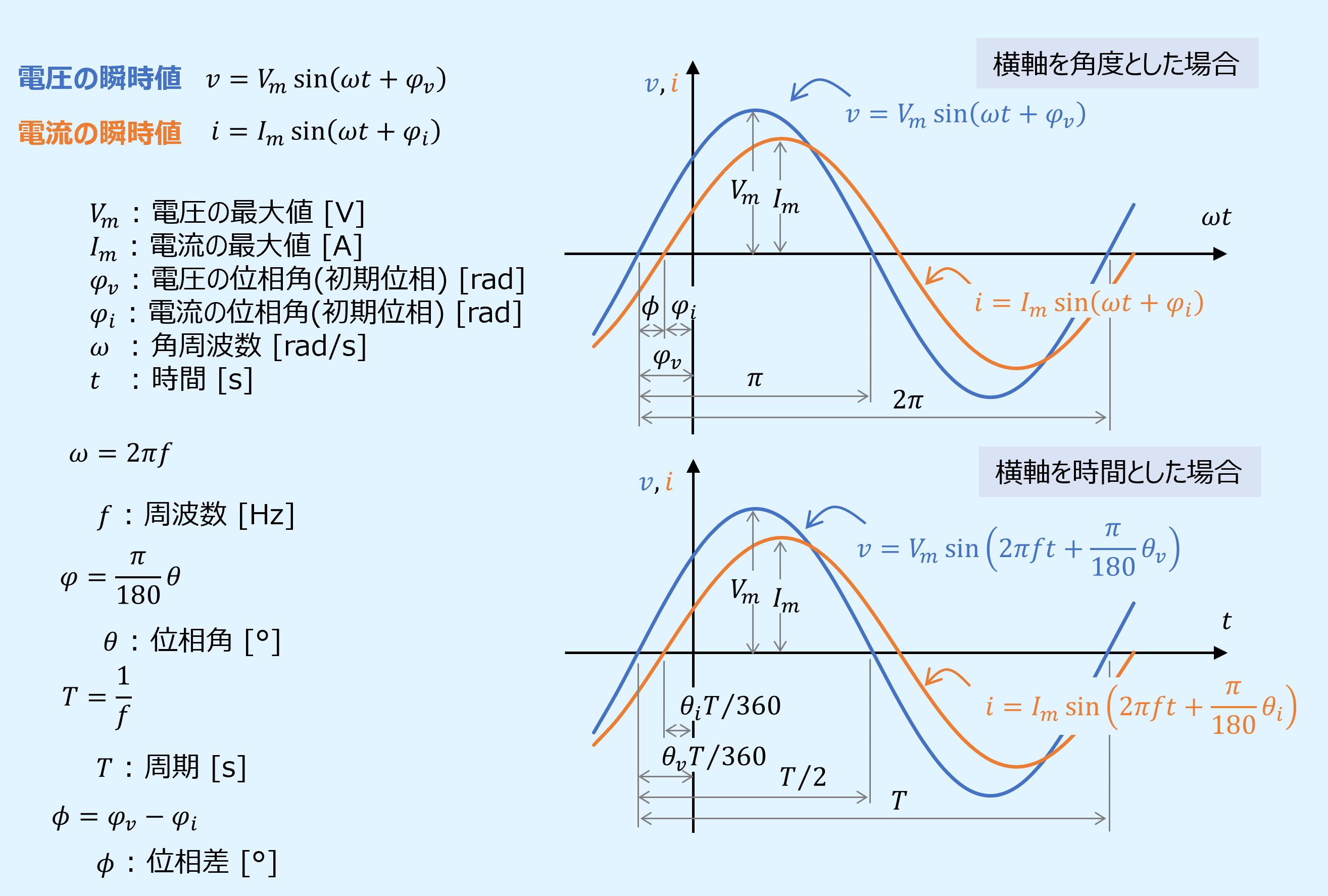
ある時間\(t\)における正弦波交流の電圧\(v\)、電流\(i\)の値を瞬時値(instantaneous value)と呼び、次式で表されます。

直流では電圧、電流の大きさだけでしたが、角周波数(angular velocity)と位相角(phase angle)という新しい要素が加わっています。

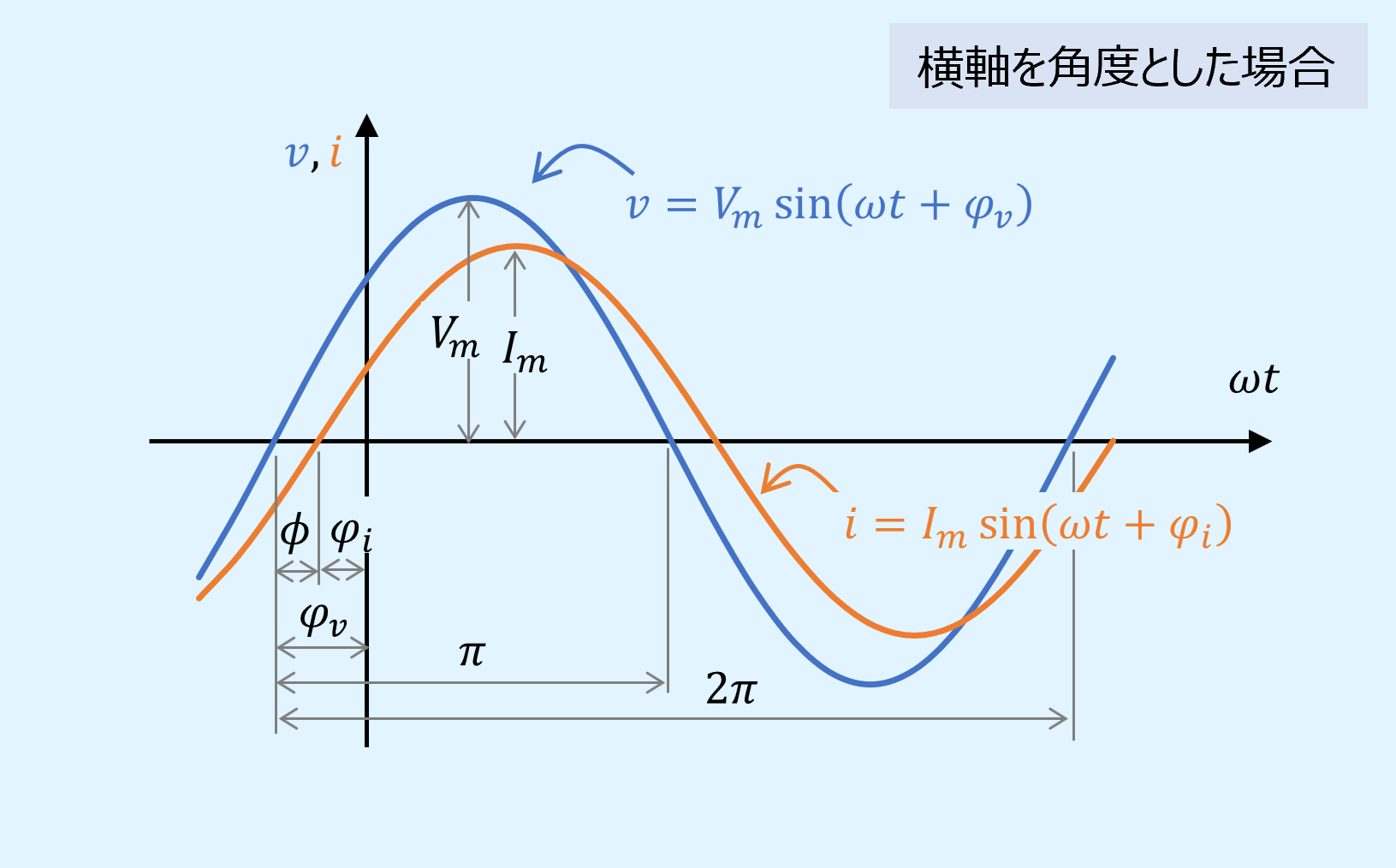
電圧と電流の瞬時値の波形をプロットすると下図のようになります。

ここで横軸は角度\({\omega}t\)としています。
こうすることで角速度\(\omega\)に依存しない表現としています。

また、交流では電圧と電流の位相が必ずしも一致しません。
これを位相差(phase difference)と呼び以下の式で表されます。

正弦波の実用的な形式

実用的には角周波数ではなく周波数(Frequency)[Hz]を用い、位相角の単位は[rad]ではなく[°]を用います。
その変換式は以下の通りです。

プログラミングで科学技術計算ライブラリを用いる場合は基本的に上式で変換して入力としますので覚えましょう。

また、周波数の逆数を周期(Period)と呼び、波形一つ分の時間長を表します。
単位は[s]です。

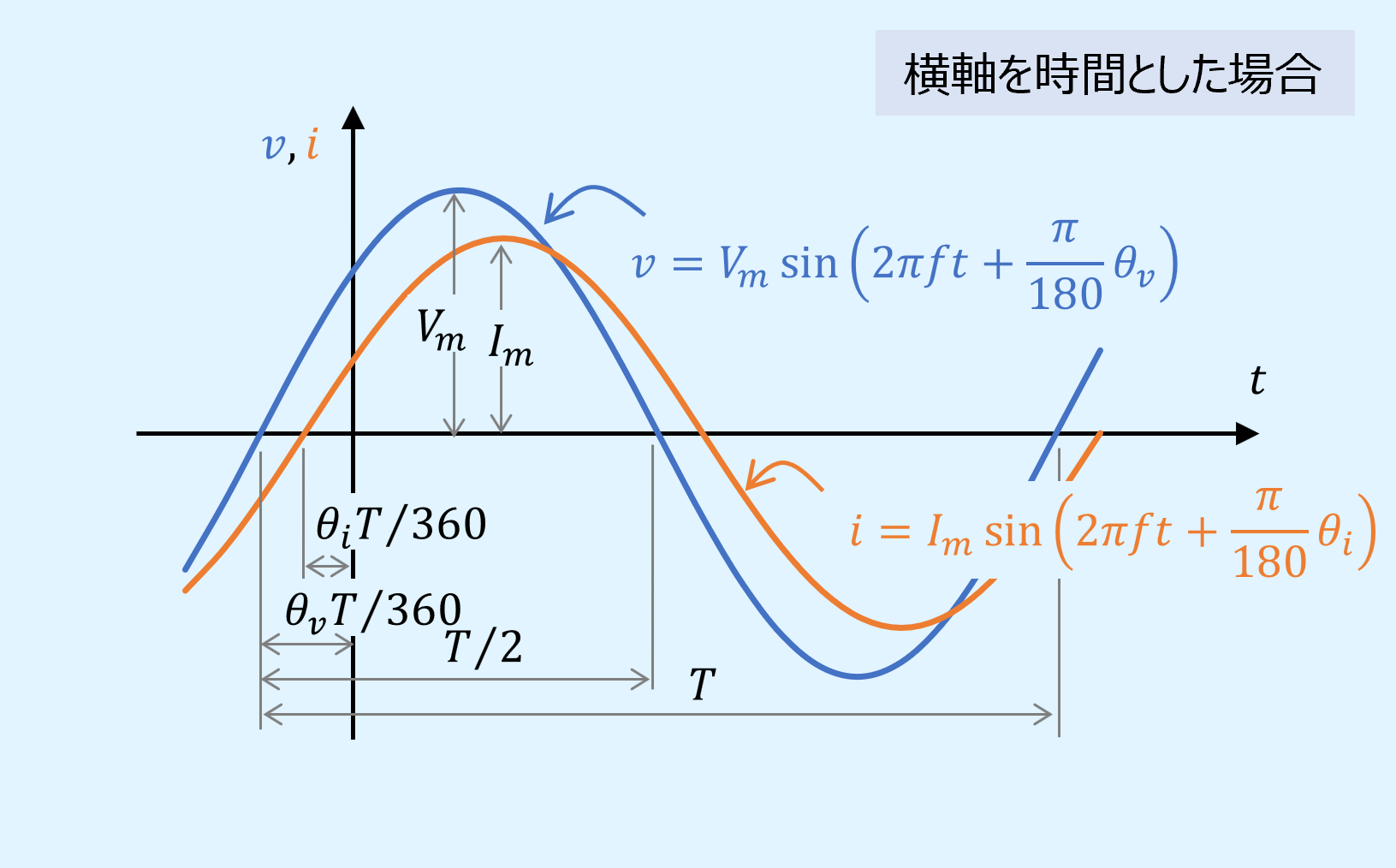
以上より、電圧と電流の瞬時値の式を角周波数から周波数に、位相角の単位を[°]とすると、以下となります。

また、波形のプロットも横軸を時間として実用的にすると以下の通りとなります。

正弦波をsin、cosどちらで表すか

正弦波を表す式として、sinの他にcosを用いることもできます。
厳密には余弦波と呼ぶべきですが、

\(\cos(x)=\sin(x+\pi/2)\)

の関係にありsinをシフトしただけであるため正弦波と呼ばれます。

cosでの表記は信号処理の分野で見られます。
周波数分析手法であるフーリエ変換では位相遅れ無しの基準成分をcosで表し、90°遅れている成分をsinで表すためです。