この記事では電気回路や信号処理で生じる波形の合成について説明をします。
最初になぜ波形の合成を考えるのかについて説明し、その後、周波数が同じ2つの正弦波を合成するとどうなるのかについて説明します。
【まとめ】波形の合成
最初にまとめです。
なぜ波形の合成について考えるのか
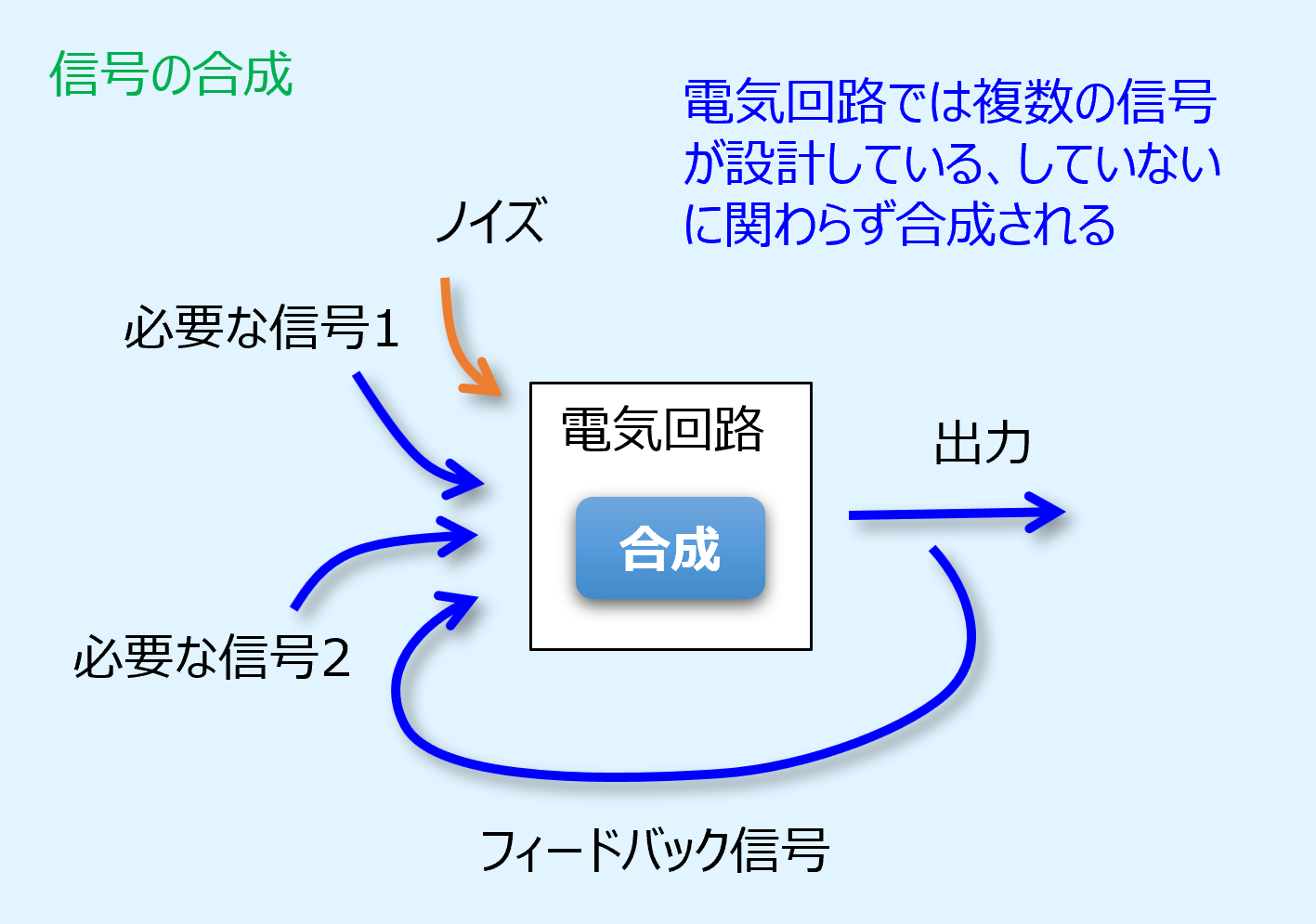
電気回路では、必要な複数の信号が合成され、所望の変形が行われて出力されます。
必要な信号には出力の一部を入力側に戻すフィードバック信号も含まれます。
また、所望外のノイズも加わります。
このように、波形の合成を行うことは電気回路の重要な役割の一つであるため、合成の結果として波形がどのような形になるのかを理解する必要があります。
本記事では正弦波で、かつ周波数は同じ2つの波形を合成するとどうなるのか、数式と図で説明を行います。
周波数が同じ2つの正弦波を合成した波形の式
最初に周波数が同じ2つの正弦波を合成した波形がどのような式になるのかを説明します。
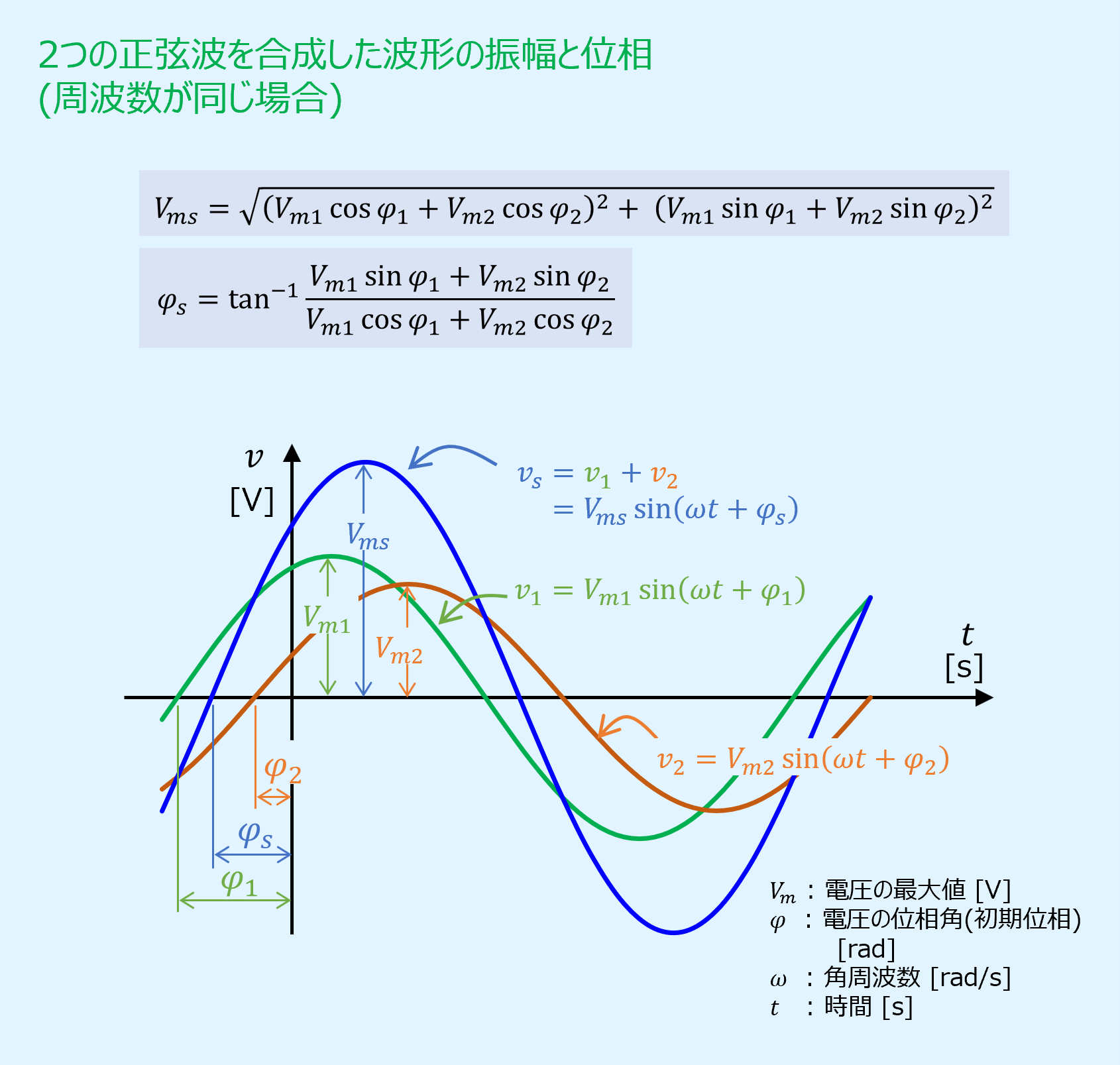
2つの正弦波を\(v_1\),\(v_2\)とし、それぞれの位相を\(\varphi_1\),\(\varphi_2\)、最大振幅を\(V_{m1}\),\(V_{m2}\)、角周波数を\(\omega\)、時間を\(t\)とすると、それらを合成した波形\(v_s\)は次のように求まります。
一方、合成波形\(v_s\)の位相を\(\varphi_s\)、最大振幅を\(V_{ms}\)とすると、次のように展開することができます。
ここで、上式(1),(2)が等しくなる条件はsin\({\omega}t\)とcos\({\omega}t\)の振幅が等しくなることなので、次の式が得られます。
最大振幅\(V_{ms}\)は、上式(3),(4)の2乗和をとると求めることができます。
また、位相\(\varphi_s\)は、上式(3),(4)の左右辺でそれぞれ割るとtan\(\varphi_s\)が得られるので、その逆正接を取ると求めることができます。
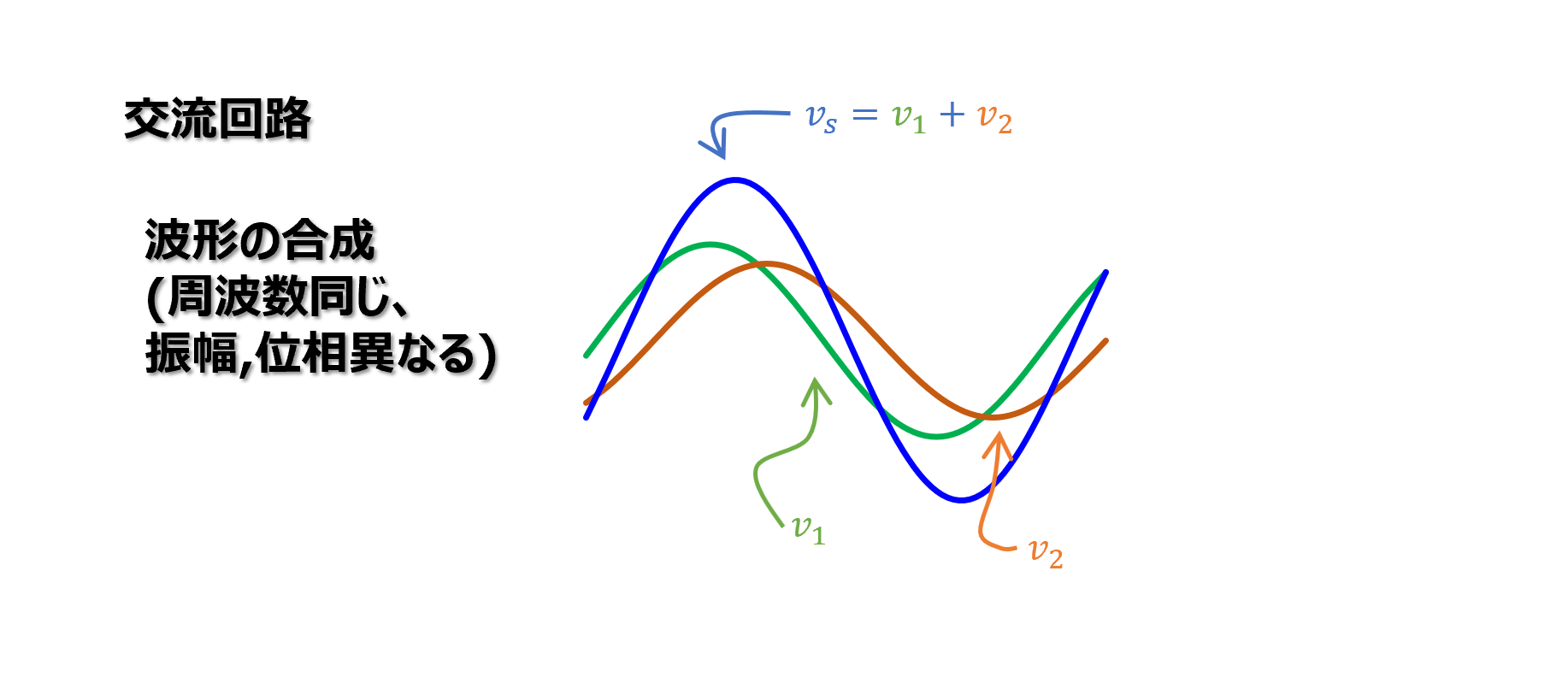
合成波形
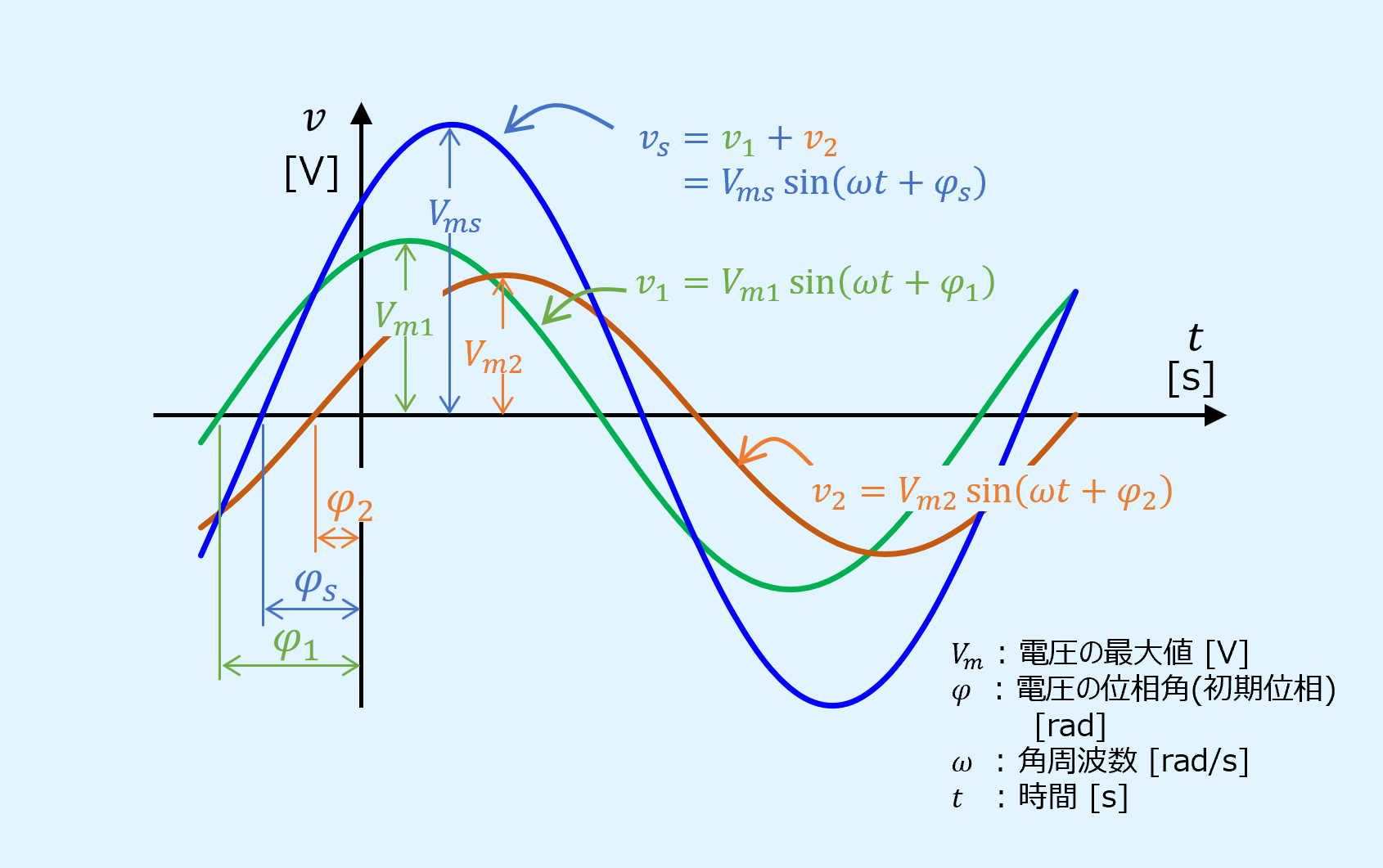
以上より、合成前の2つの正弦波\(v_1\),\(v_2\)と、合成後の波形\(v_s\)を図示すると以下となります。
周波数が同じであれば、振幅と位相が異なる同じ周波数の正弦波になります。
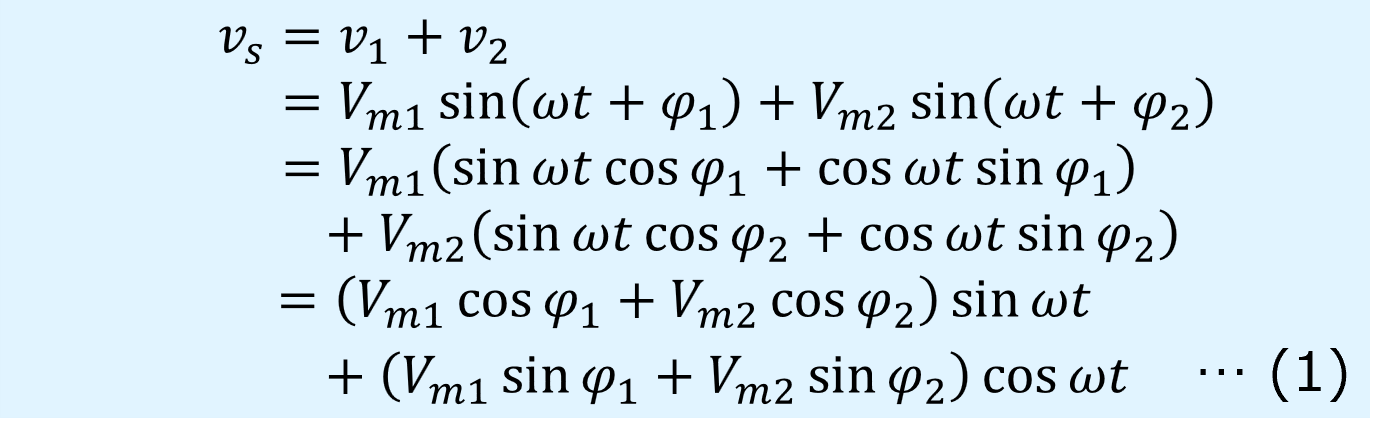
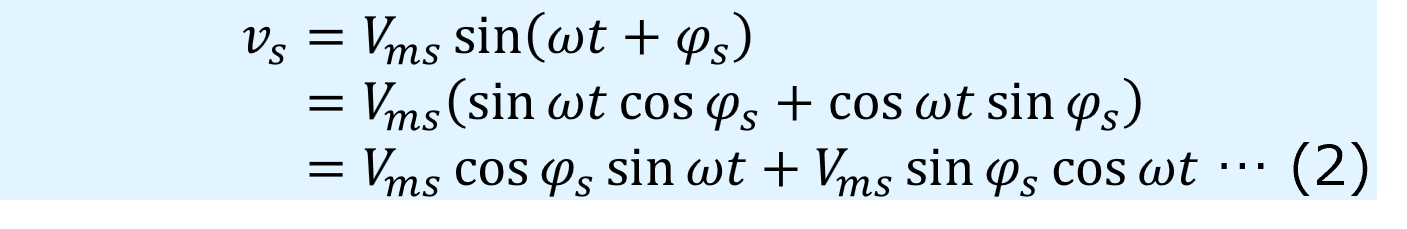
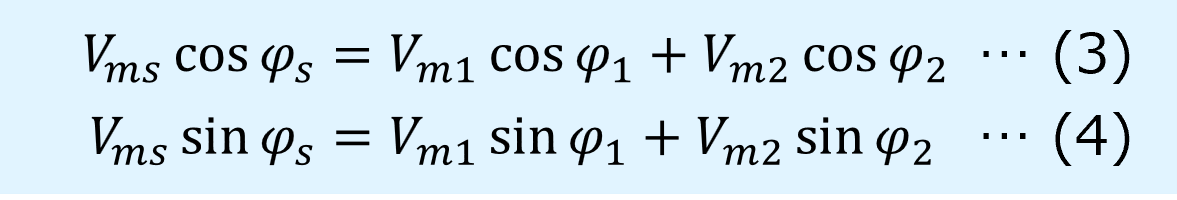
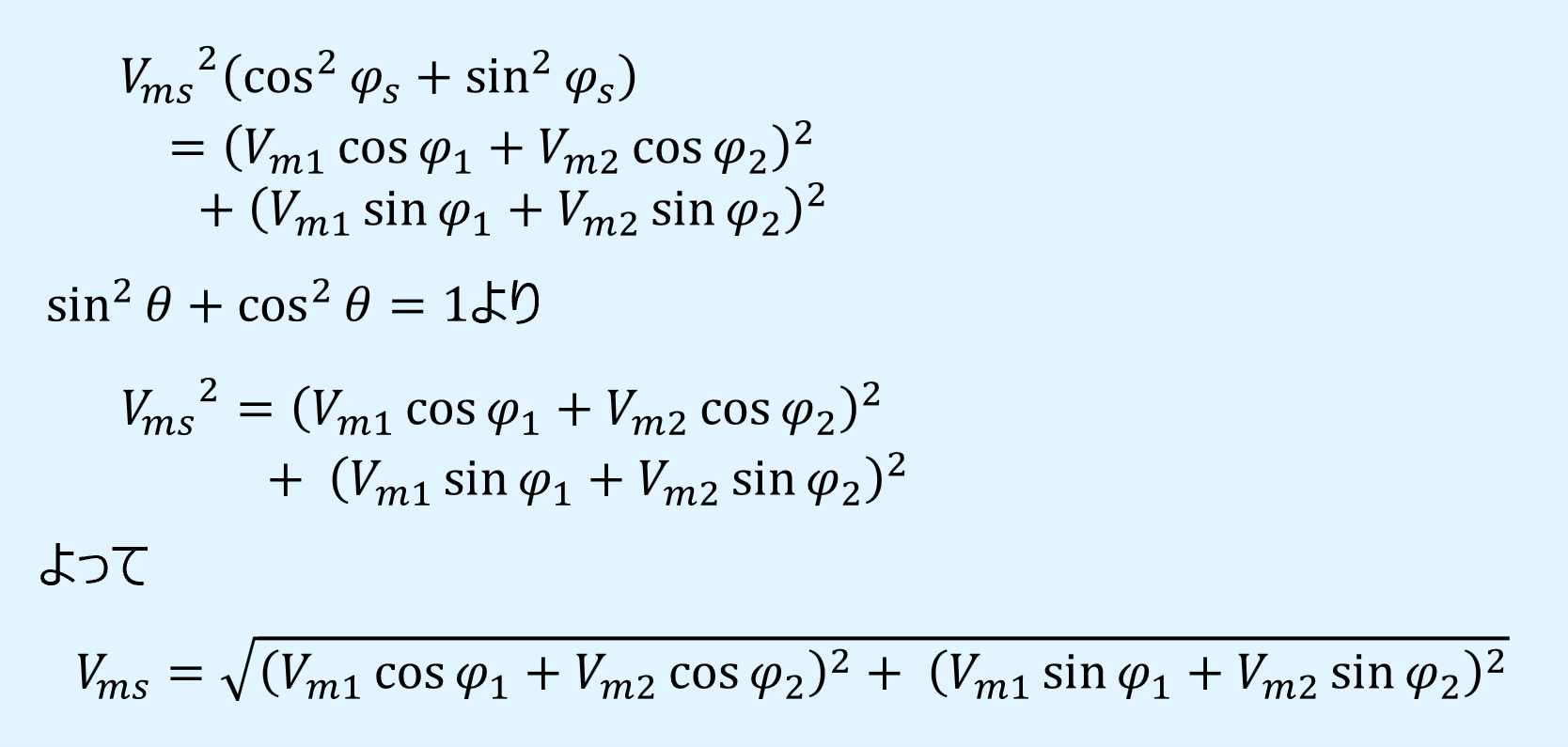
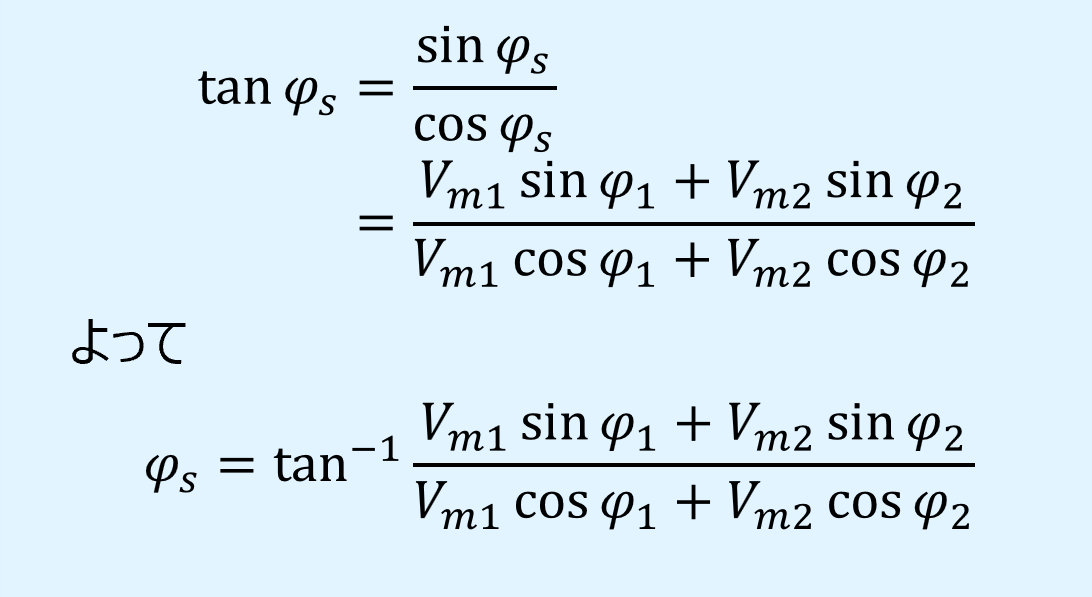

コメント