この記事では電気回路で用いられるフェーザ表示について説明をします。
フェーザ表示の必要性から、フェーザ表示とは何のか、ベクトルとしての表現方法の種類までを扱っています。
【まとめ】フェーザ表示
最初にまとめです。
フェーザ表示の必要性
電圧と電流の正弦波を以下に示します。
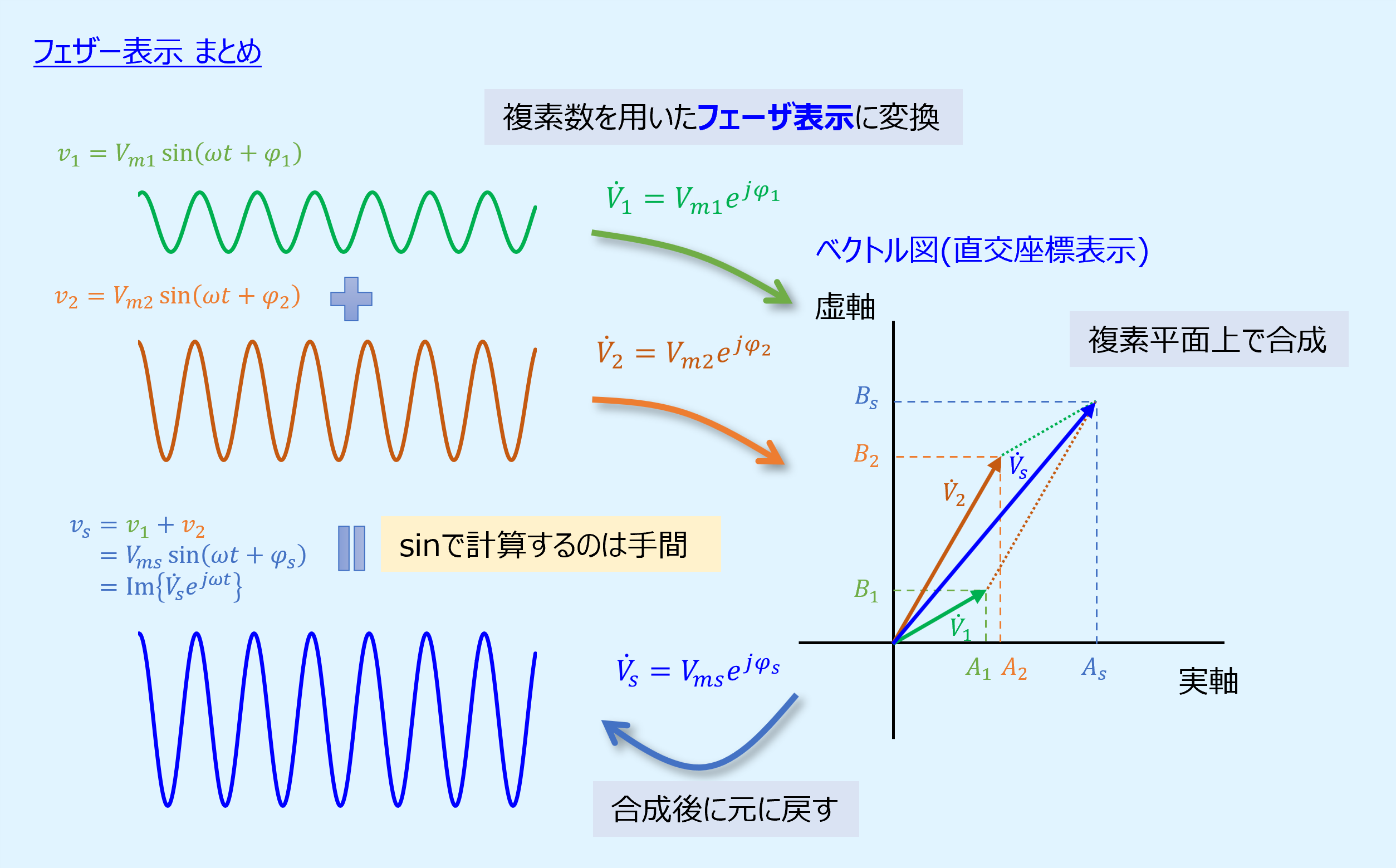
この正弦波の波形を複数合成しようとすると、2つくらいなら何とかなりますが、3つ、4つと増えると手間がかかり大変です。
そこで、計算を簡単にするためフェーザ表示を用います。
複素数を利用する
基本的に、電気回路では入力信号の周波数と同じ周波数が回路内部で処理され、出力されます。
また、電圧と電流が異なる周波数となることもあり得ません。
このことから、周波数は前提条件として扱われるものといえます。
また常識的なことですが、時間\(t\)についても、電圧、電流を違う時間で比較したり、回路の入力、内部、出力を違う時間で比較したりはしないので、前提条件とするものです。
以上から、前提条件とならず、回路で変化するものは振幅と位相のみであり、これらがどのような値になっているのかさえ分かれば実用的には数式でsinを用いなくてもよいことになります。
ではsinを用いずにどうするのかというと、複素指数関数\(e^z\)に変換して計算を行います。
ここで、\(z\)は複素変数であり実部を\(x\)、虚部を\(y\)とすると\(z=x+jy\)となります。\(j\)は複素数を表しています。
具体的には、以下の式のように、振幅と位相を複素指数関数に当てはめます。
複素数から正弦波に戻す方法
複素数に変換して、計算した後は、元の正弦波に戻せないと意味がありません。
戻す方法を次に説明します。
式(3)は以下のように変形ができます。
ここで、上式の変形は以下のオイラーの公式を利用しています。
式(4)の右辺第2項の虚数部を見ると、正弦波となっていることが分かります。
このことを利用し、式(4)を用いて式(1)を以下のように書くことができます。
ここで、Im(\(z\))は複素変数\(z=x+jy\)の虚部\(y\)を表す記号です。
式(5)から、波形を複素数に変換しても、虚数部を取れば元の正弦波に戻すことができます。
フェーザ表示
式(3)は次のように変形することができます。
\(\dot{V}\)をフェーザ表示またはフェーザ(phasor)と呼びます。
このフェーザの部分のみで計算を行います。
ベクトルの直角座標表示と極座標表示
フェーザは大きさと正負の方向を持つベクトルです。
ベクトルには実数部と虚数部で表す直交座標表示と、振幅と位相で表す極座標表示があります。
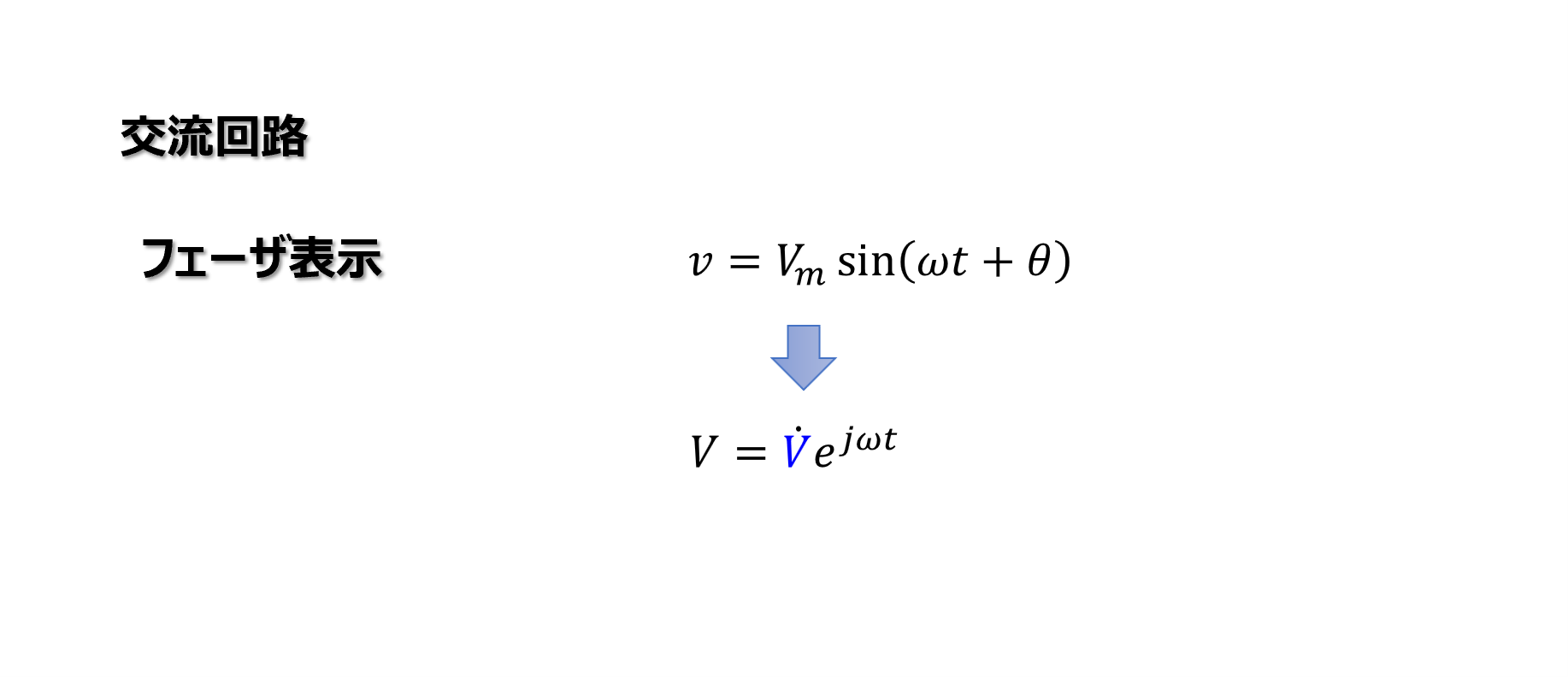
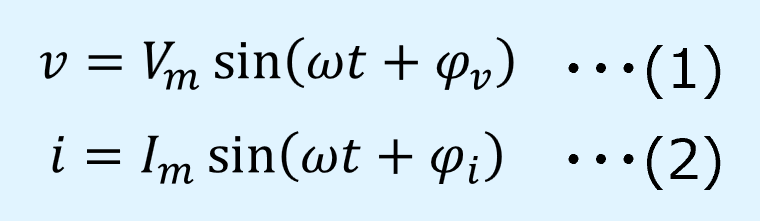

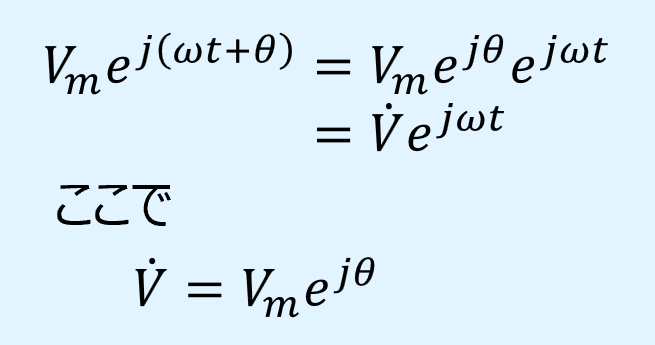
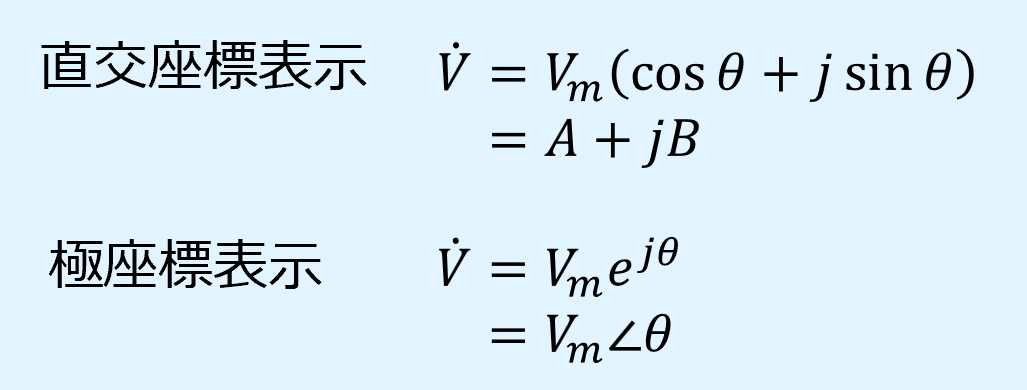

コメント