この記事では電気回路の一つである直流回路について、演習問題の解説をします。
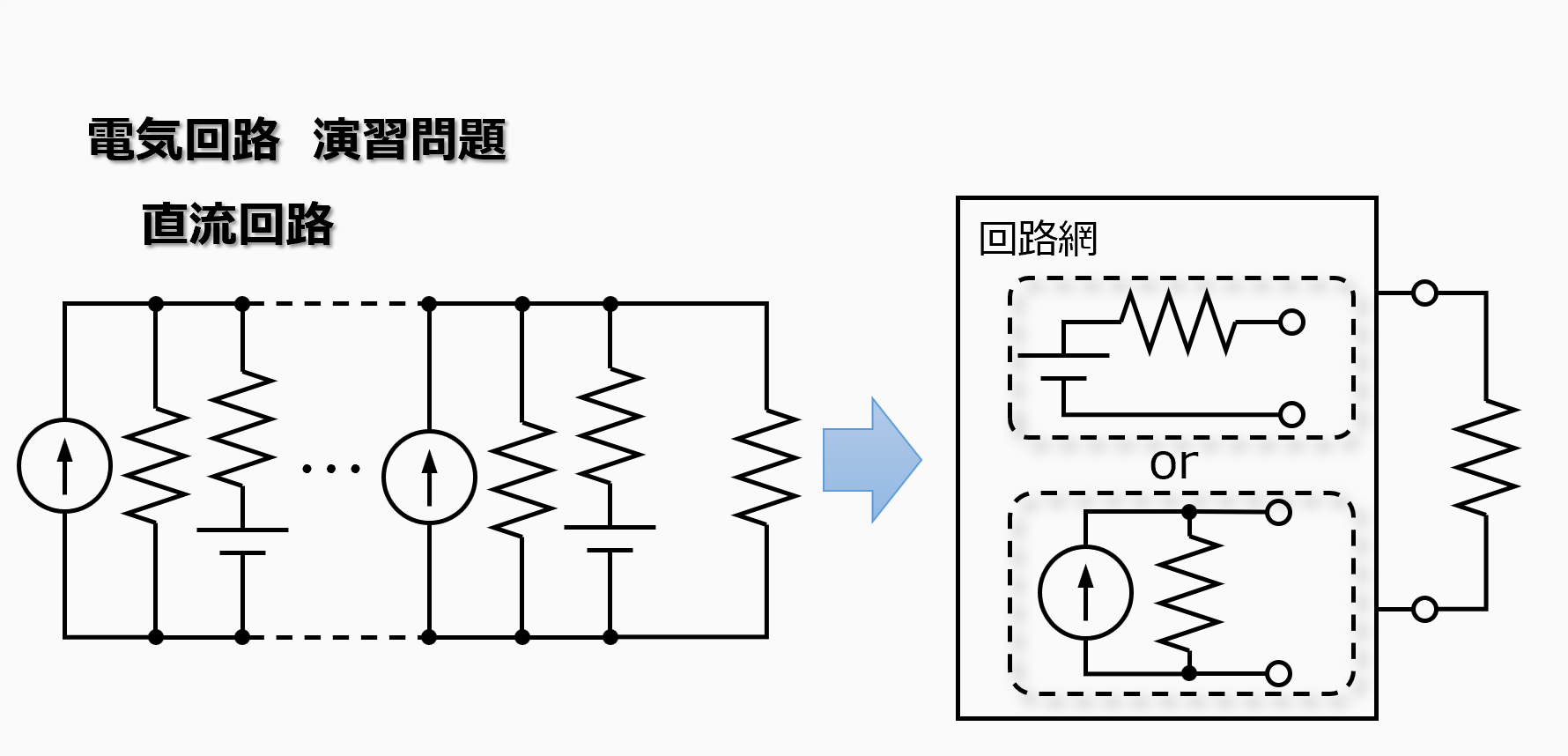
電源が3つ以上、抵抗4つ以上から成る回路を等価電源回路に置換します。
等価電源回路への変換
複雑な電源回路網も電圧源と電流源の相互変換を繰り返すと、電圧源と抵抗の直列接続か電流源とコンダクタンスの並列接続の等価回路に変換ができます。
その手順は以下の通りとなります。
- 直列している電圧源と抵抗を合成する。
- 電圧源をノートンの法則に従って電流源に変換する。
- 並列している電流源とコンダクタンスを合成する。
- 電流源をテブナンの定理に従って電圧源に変換する。
- 1~4を繰り返す
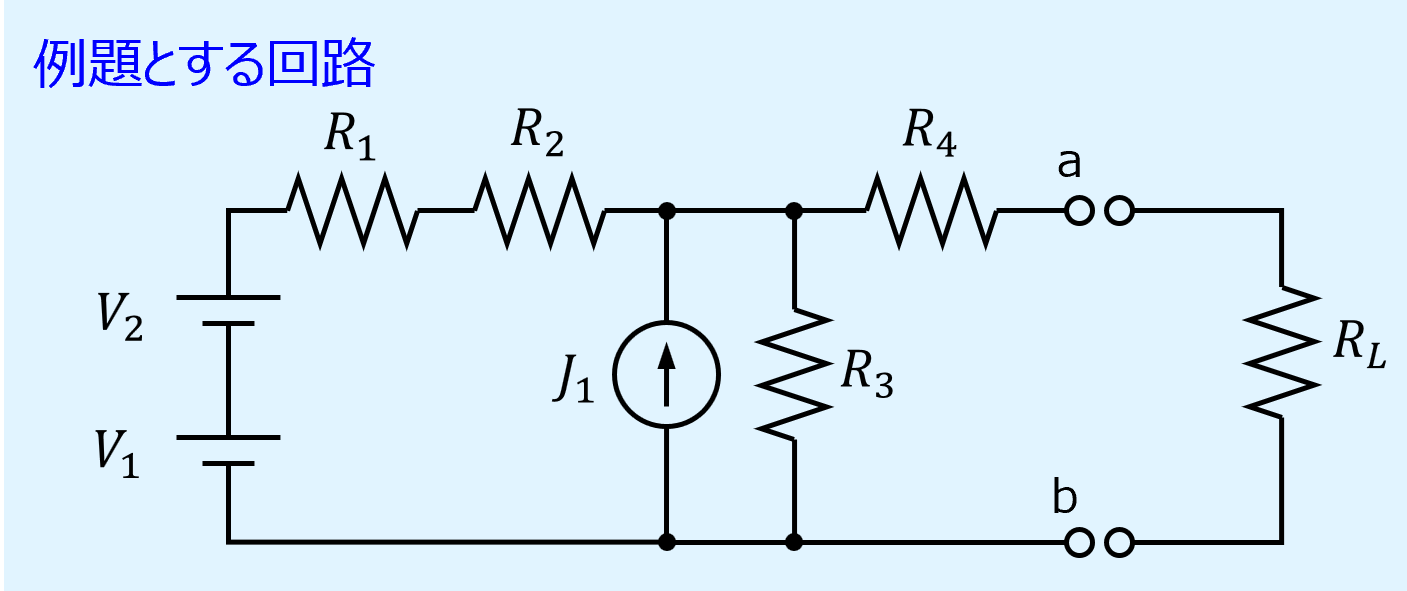
等価電源回路の例題
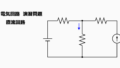
先述の等価電源回路の求め方の例題として、以下の回路のa,b間について等価回路に変換してみます。
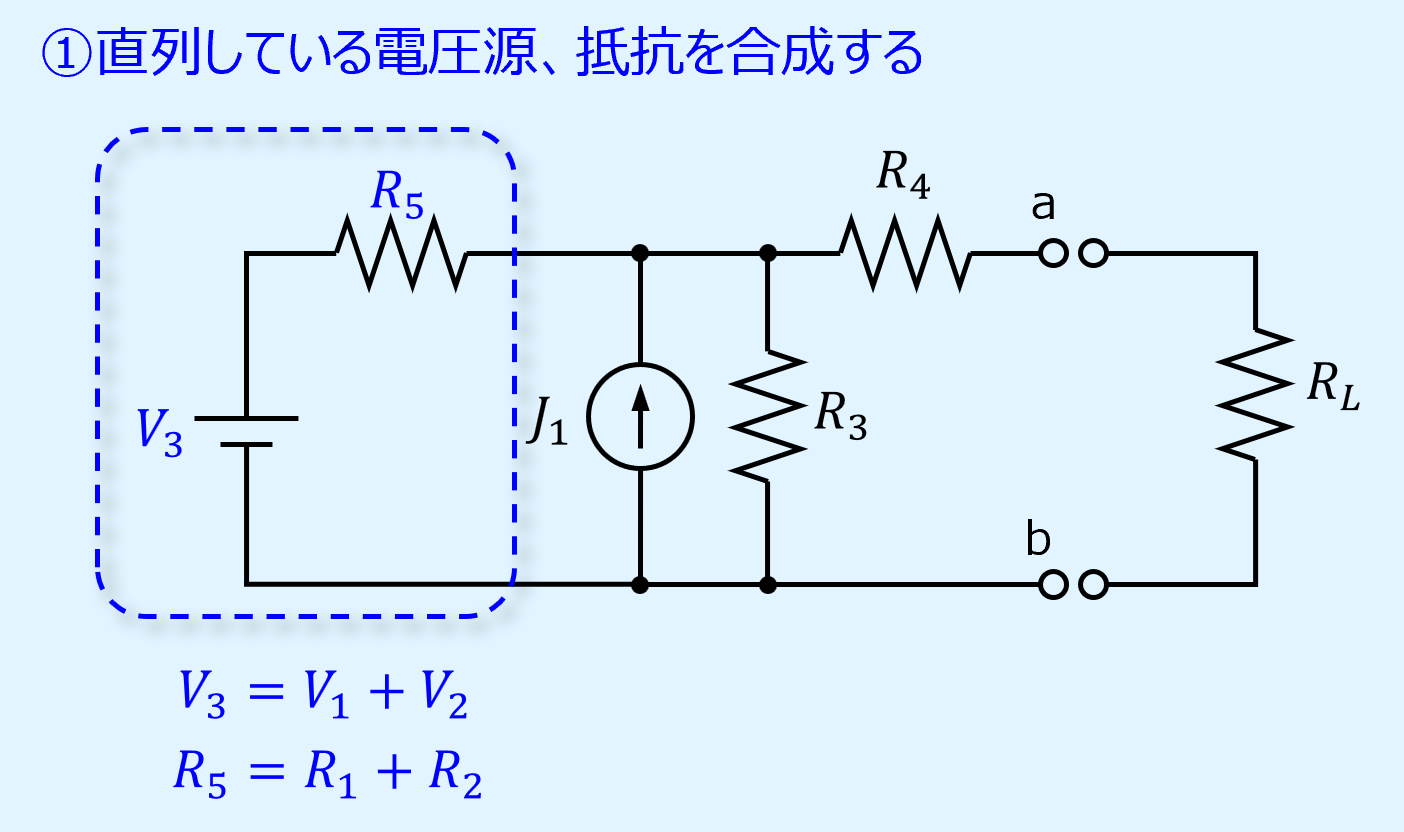
まず直列している電圧源と抵抗を合成します。
ここでは\(V_1\)と\(V_2\)を合わせて\(V_3\)に、\(R_1\)と\(R_2\)を合わせて\(R_5\)にしています。
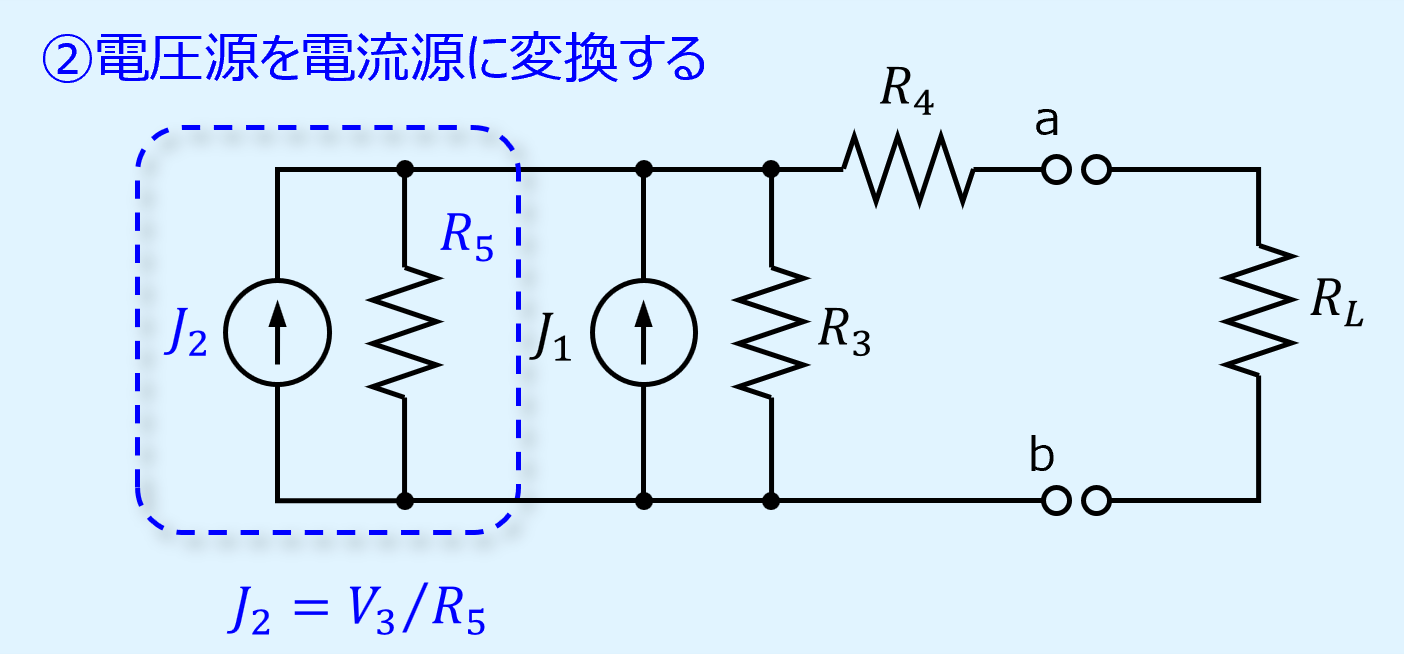
次にノートンの定理により、電圧源を電流源に変換します。
\(R_5\)はそのまま並列抵抗となり、\(V_3\)を\(R_5\)で割ると\(J_2\)が電流源となります。
これにより抵抗と電流源が並列に並びますので、合成が可能となります。
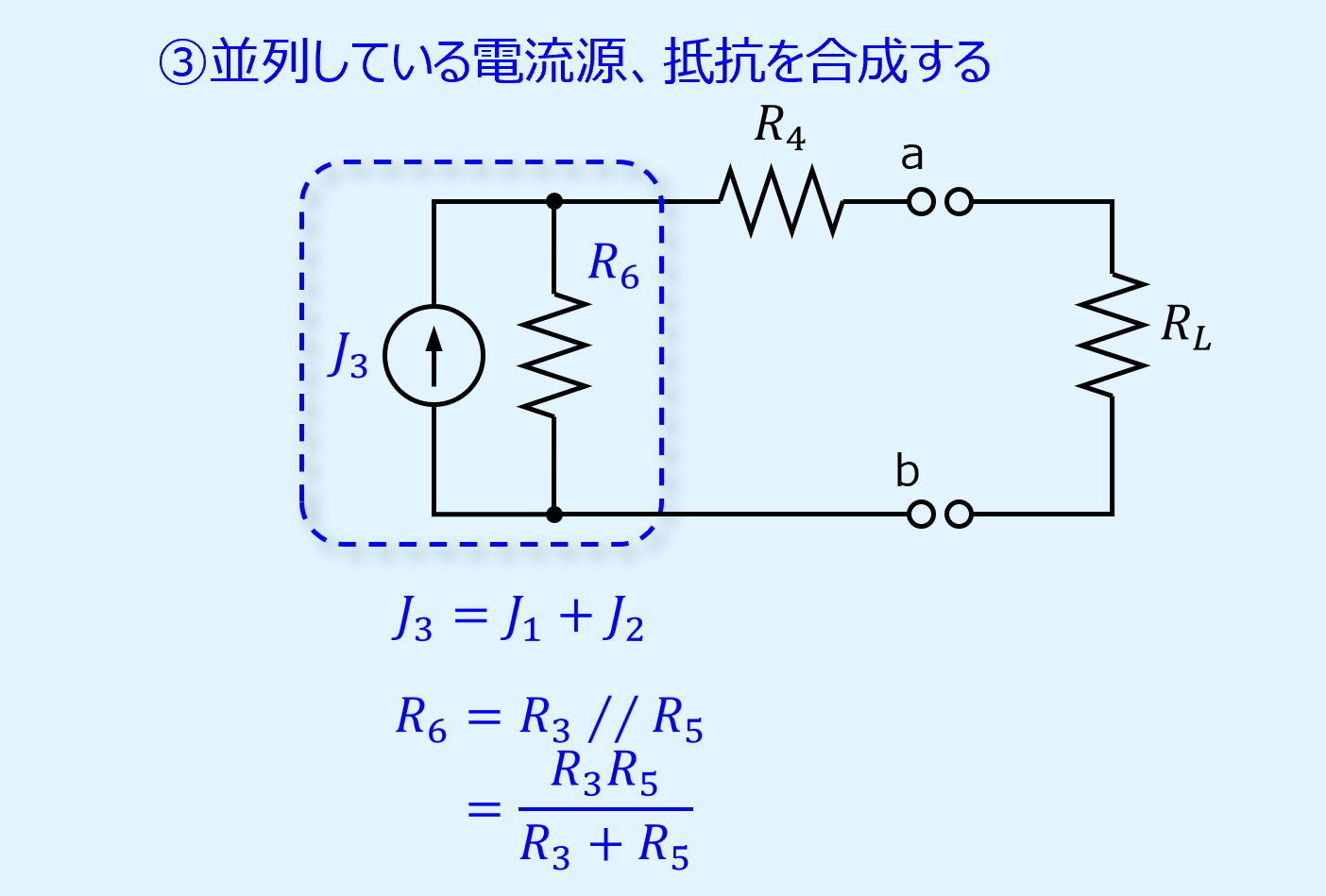
次に並列接続となっている電流源と抵抗を合成します。
ここでは\(J_1\)と\(J_2\)を合わせて\(J_3\)に、\(R_3\)と\(R_5\)を合わせて\(R_6\)となります。
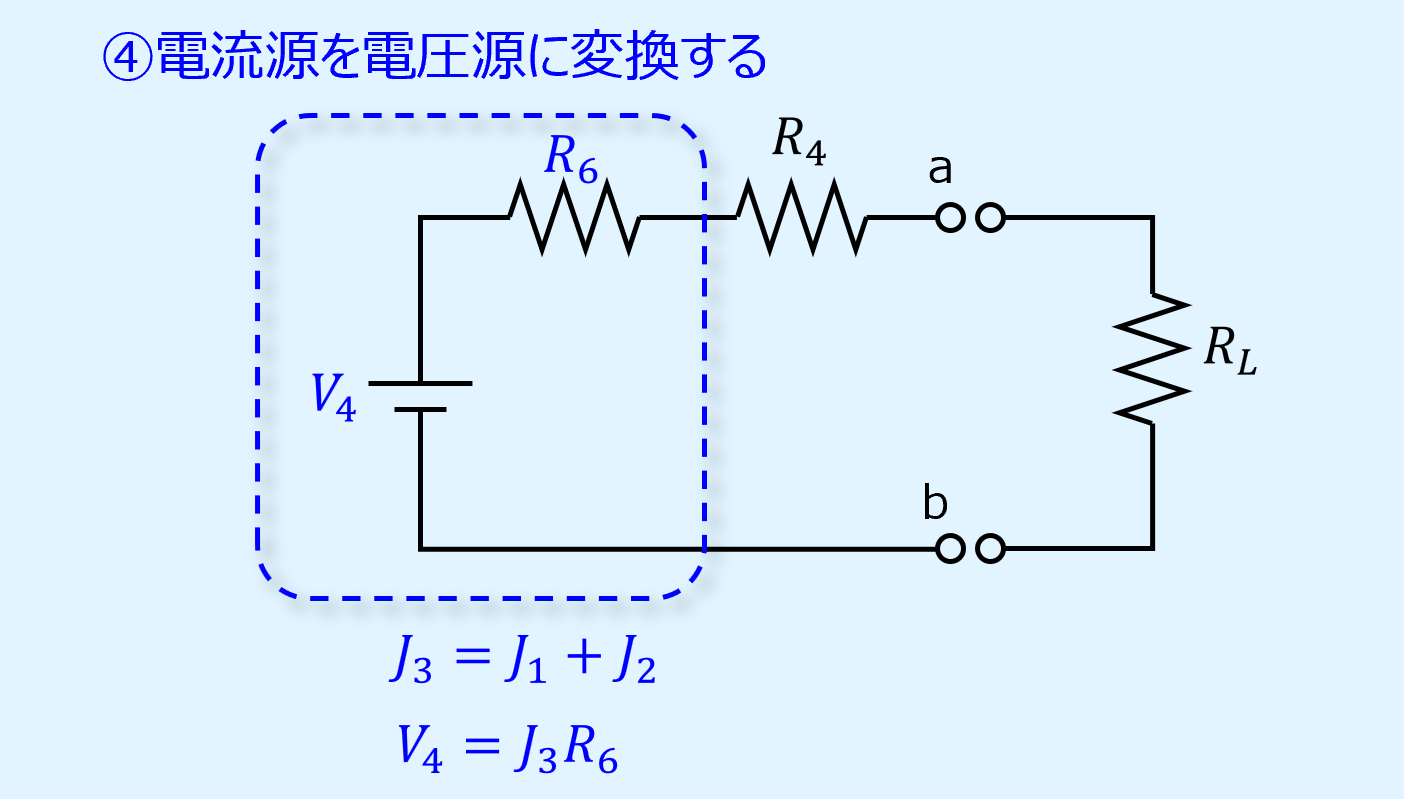
次にテブナンの定理により、電流源を電圧源に変換します。
\(R_6\)はそのまま直列抵抗となり、\(J_3\)に\(R_6\)をかけると電圧源\(V_4\)となります。
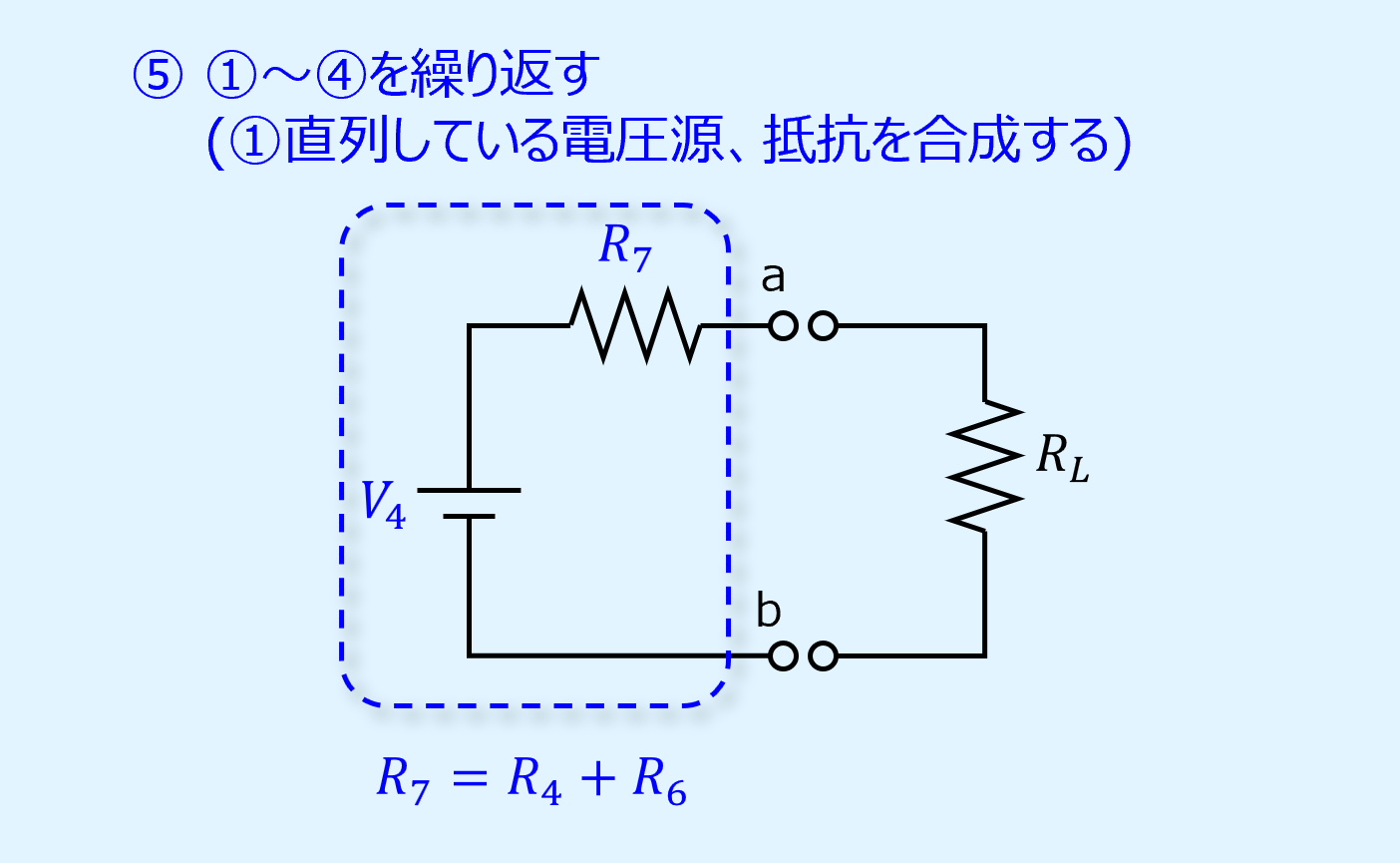
以降、同じ手順を繰り返すことになります。
ここではもう一回直列抵抗を合成して終わりとなります。
\(R_4\)と\(R_6\)を合わせて\(R_7\)が得られます。
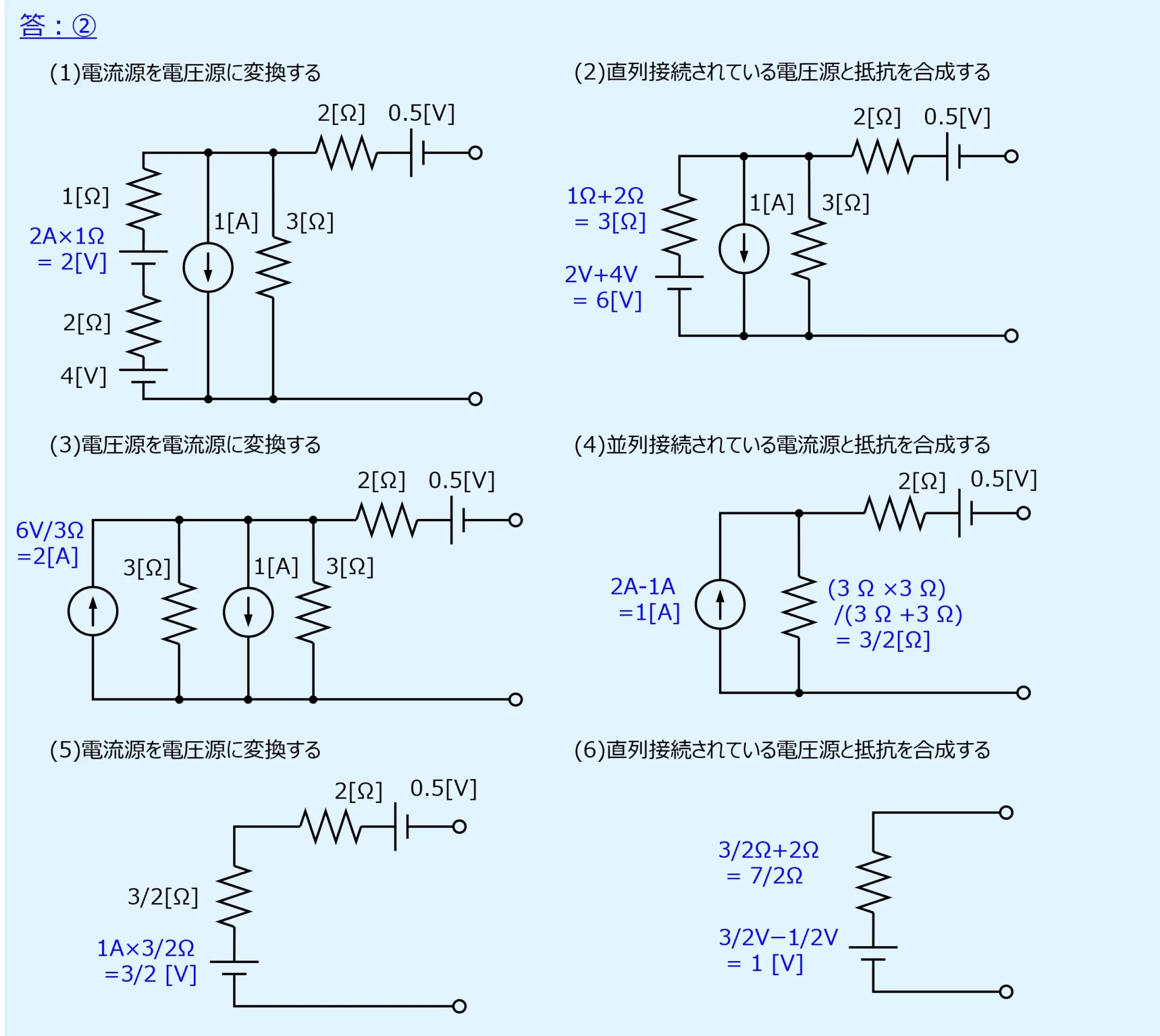
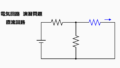
演習問題1
電圧源2つ、電流源2つ、抵抗4つから成る直流回路の問題を以下に示します。
下図のように、電流源を電圧源に変換、合成、電圧源を電流源に変換、合成、を繰り返して等価回路に置換します。
その他
電気回路全般については以下をご覧下さい。

コメント