この記事では数学や情報処理で用いられる集合の演算ついて説明をします。
数式に加えて、関係を図示する方法まで取り扱います。
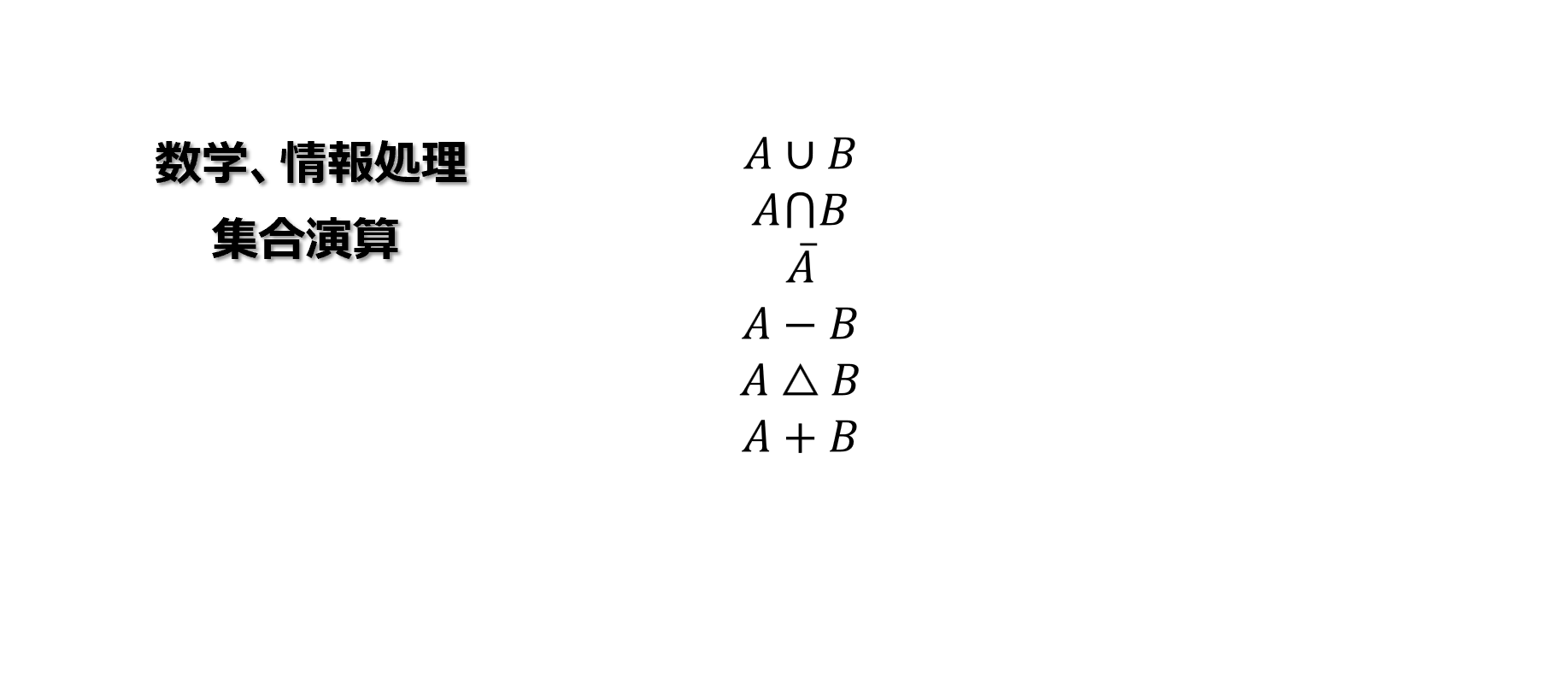
【まとめ】集合演算
和集合
集合\(A\),\(B\)の要素を全部よせ集めて得られる集合を和集合(union)といい、次のように表します。
記号「\(\cup\)」は結び(joinまたはcup)と読みます。
和集合に内包的記法を用いると以下のように書けます。
和集合の例を以下に示します。
共通集合
集合\(A\),\(B\)の両方に共通な要素の集合を共通集合(intersection)といい、次のように表します。
記号「\(\cap\)」は交わり(meetまたはcap)と読みます。
共通集合を内包的記法を用いると以下のように書けます。
和集合の例を以下に示します。
補集合
全体集合\(U\)に属するが、集合\(A\)には属さない要素の集合を補集合(complementary set)といい、次のように表します。
補集合を内包的記法を用いると以下のように書けます。
また、上式のように全体集合Uが推測できる場合にはUを明示しないことがあります。
補集合の例を以下に示します。
差集合
集合\(A\)の要素のうち、集合\(B\)の要素で無いものの集合を差集合(set difference)といい、次のように表します。
差集合を内包的記法を用いると以下のように書けます。
また、差集合\(A-B\)は\(A\cap\bar{B}\)とも表現することができます。
差集合の例を以下に示します。
対称差
集合\(A\)の要素であって集合\(B\)の要素でない、または、集合\(B\)の要素であって集合\(A\)の要素でない、ものの集合を対称差(symmetric difference)といい、次のように表します。
対称差は差集合\(A-B\)と\(B-A\)の和集合なので次のように表現することができます。
対称差の例を以下に示します。
直和
集合\(A\)と\(B\)が共通の要素をもたないとき、\(A\)と\(B\)は互いに素であるといいます。
互いに素な集合の和を直和(direct sum)といい、次のように表します。
直和の例を以下に示します。
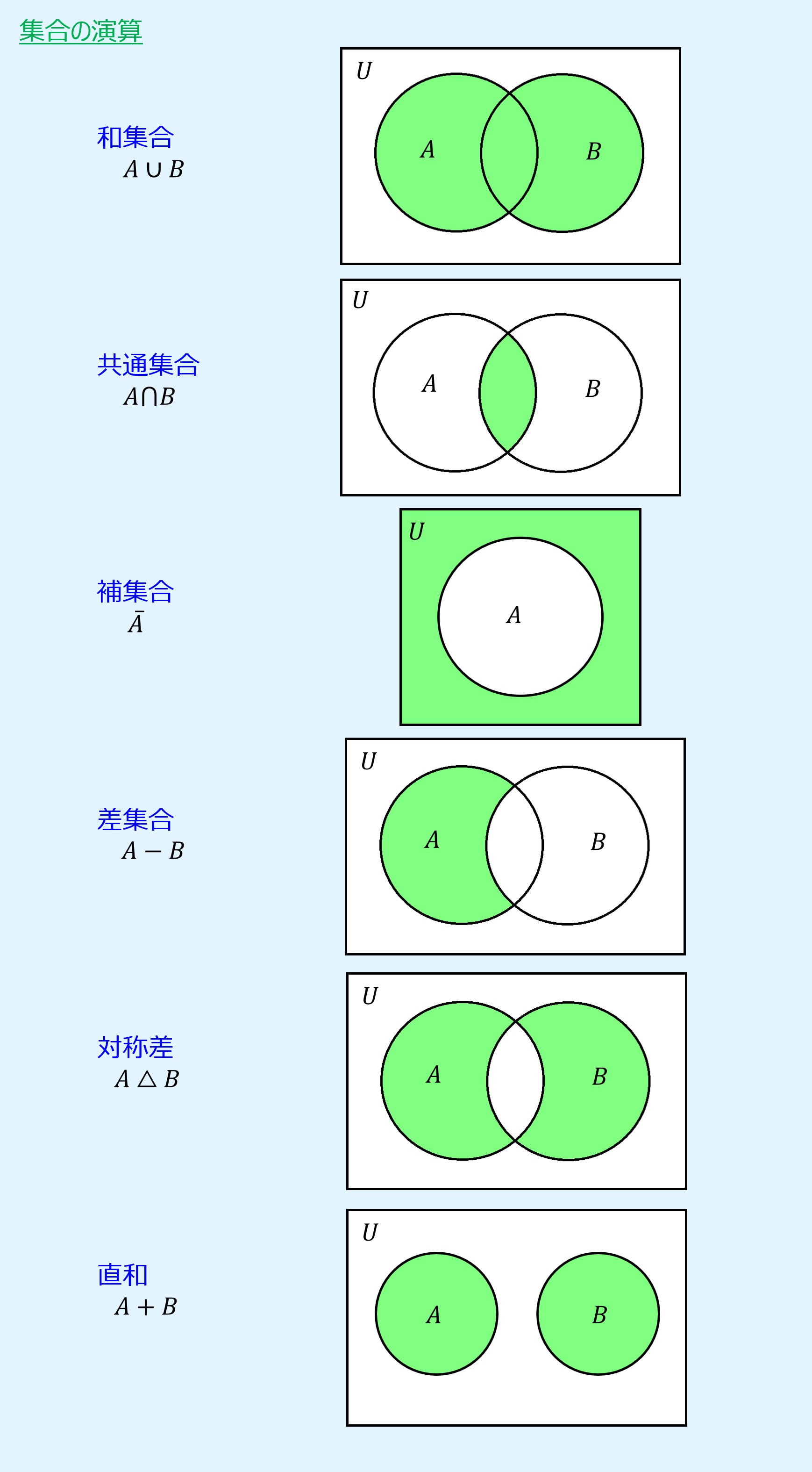
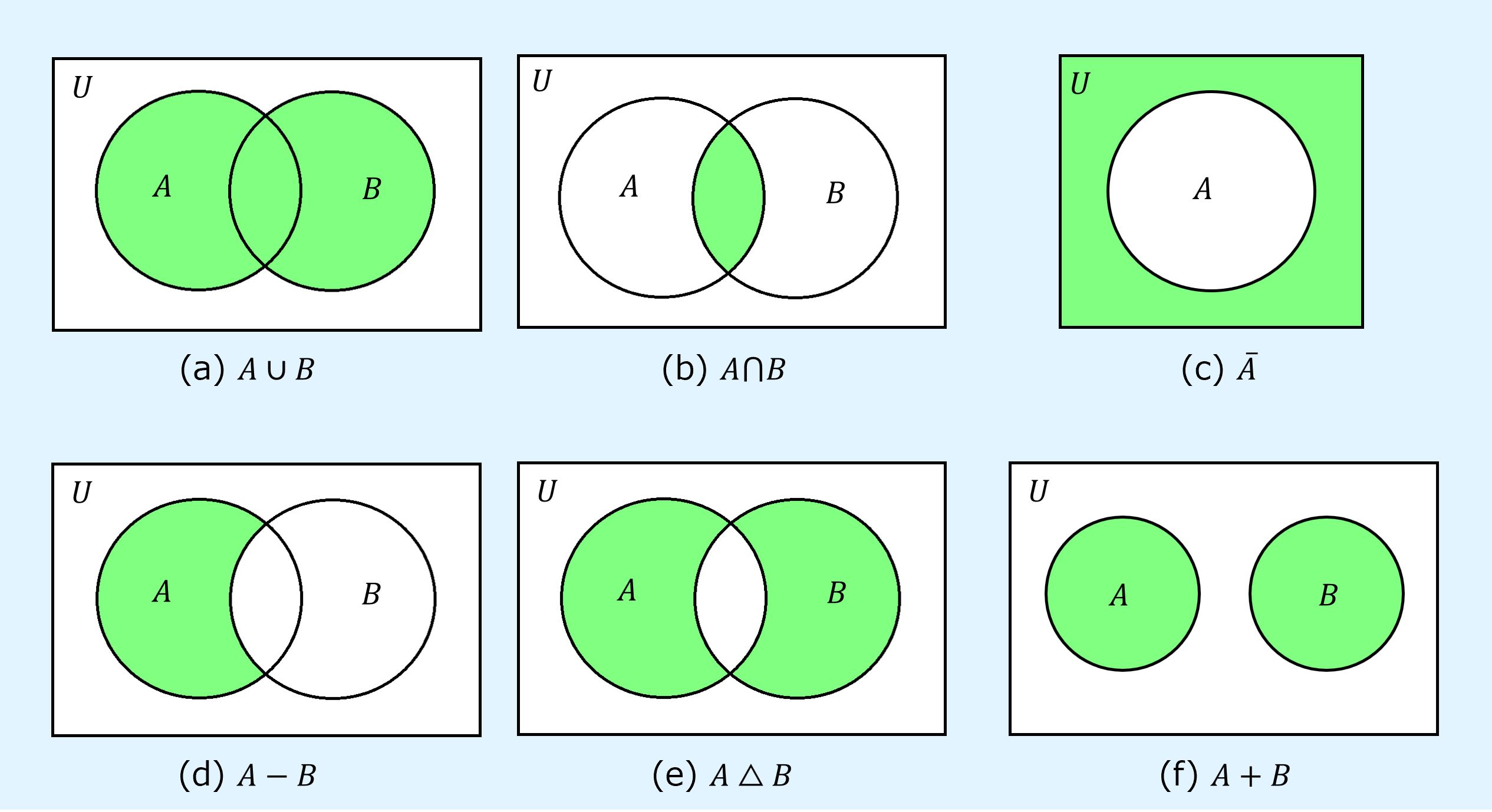
ベン図
集合の演算はベン図(Venn diagram)を用いて図示すると分かりやすい場合があります。
ベン図を用いて和集合、共通集合、補集合、差集合、対称差、直和を表すと以下のようになります。
演算の順番
和集合、共通集合、差集合、対称差、直和は2項演算、補集合は1項演算となっています。
そのため、式計算においては1項演算である補集合から優先して計算されます。
その他
集合演算と論理演算全般については以下をご覧下さい。

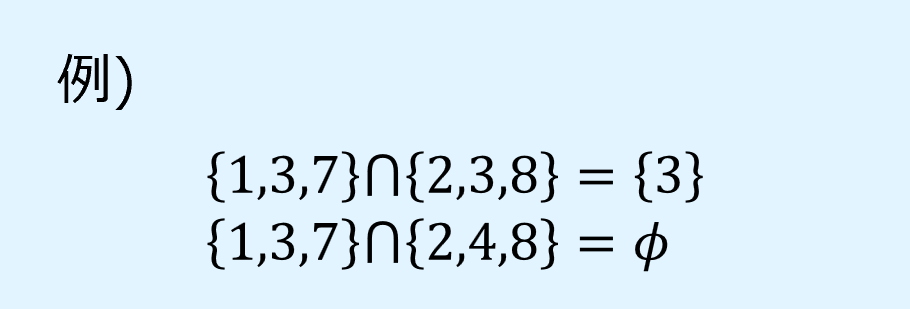


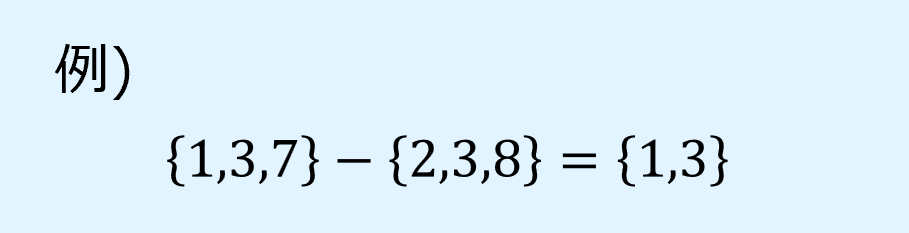
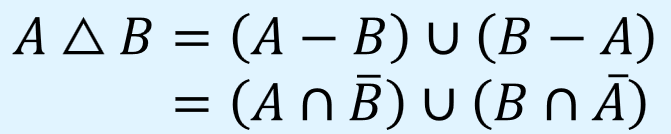

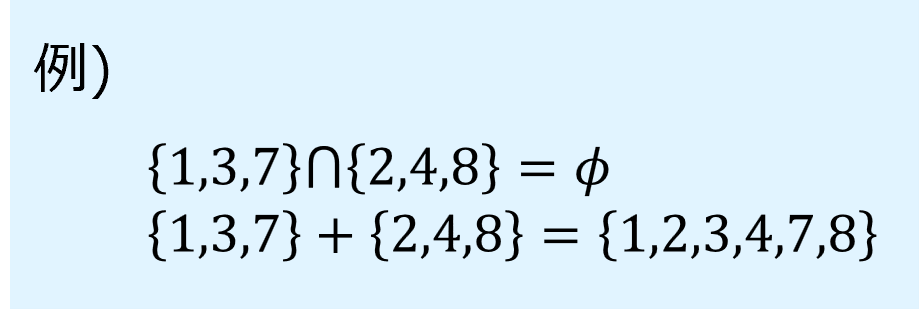


コメント