この記事では電気回路の一つである直流回路について、演習問題の解説をします。
電圧源2つと抵抗2つを並列接続した回路を取り扱います。
並列接続端の開放電圧と短絡電流を求めます。
解説用の回路
演習問題の前に、対象となる回路の解説を行います。
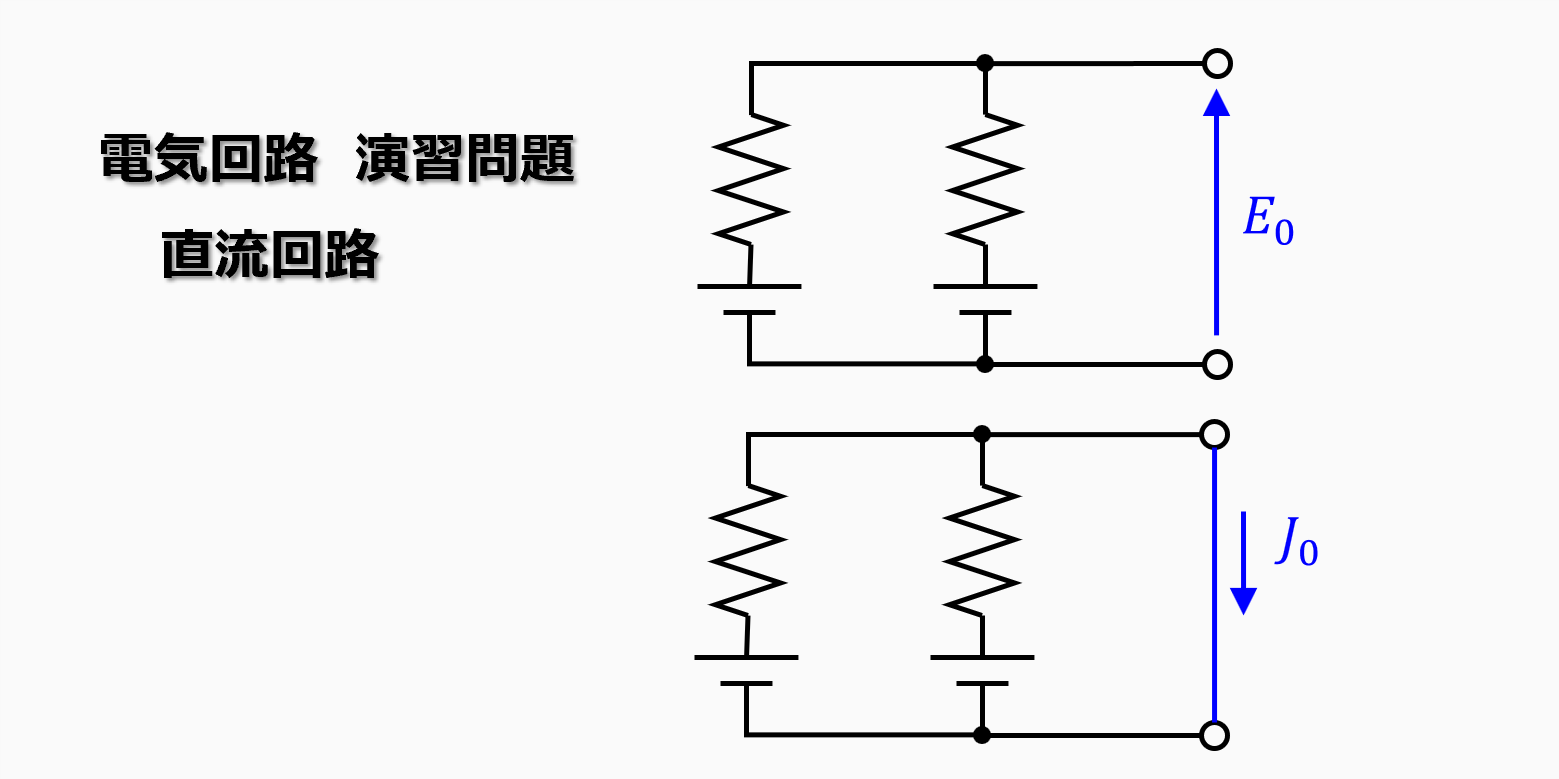
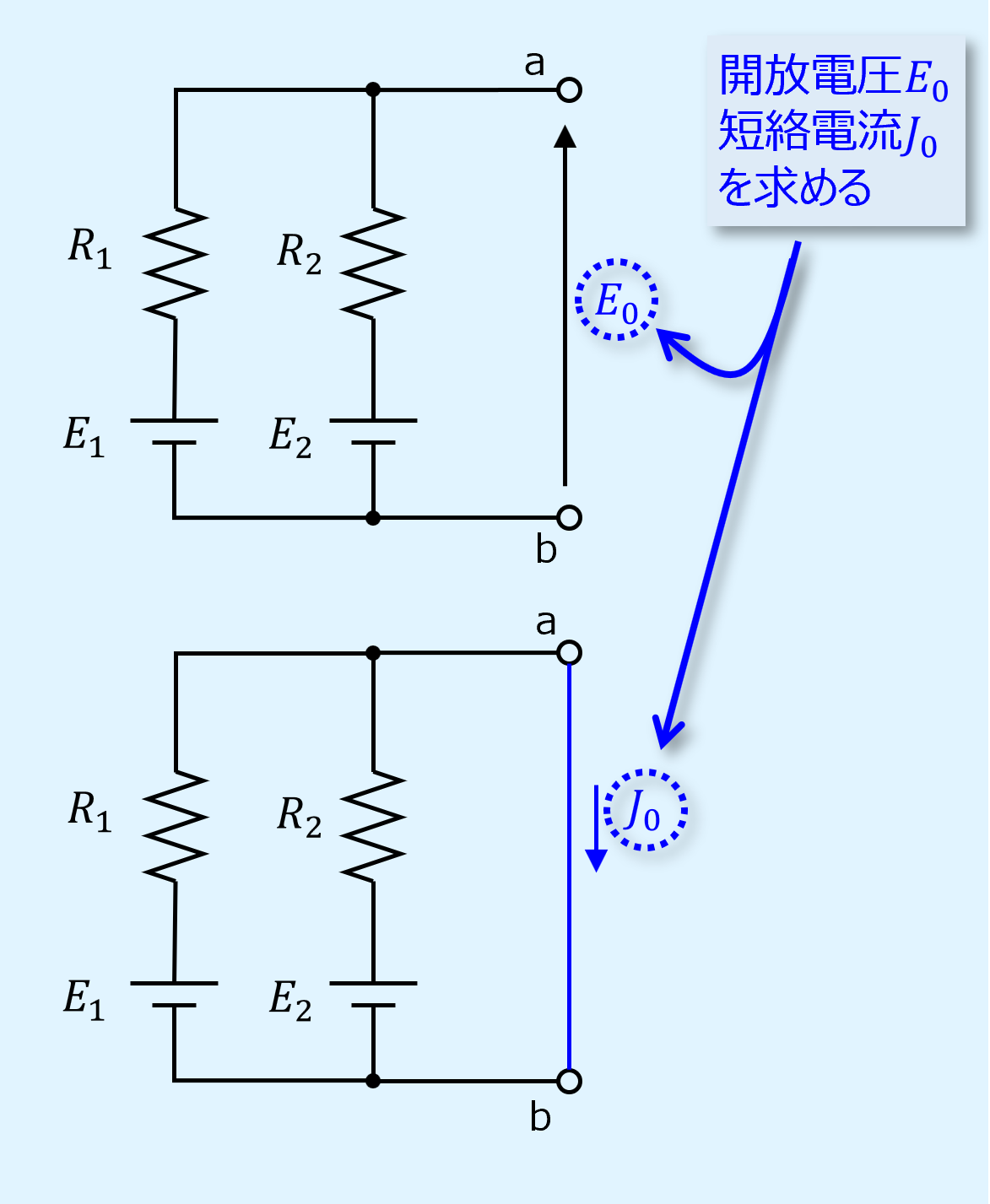
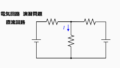
解説用の回路は以下となります。
電圧源2つ、抵抗2つから成る回路です。
ここで求めるのはa,b端の開放電圧\(E_0\)と短絡電流\(J_0\)です。
開放電圧\(E_0\)と短絡電流\(J_0\)を求める解法は2つあり、キルヒホッフの法則と電圧源と電流源の相互変換を用いる方法となります。
解法1:キルヒホッフの法則
キルヒホッフの第2法則(電圧則)より開放電圧を求め、キルヒホッフの第1法則(電流則)より短絡電流を求める方法です。
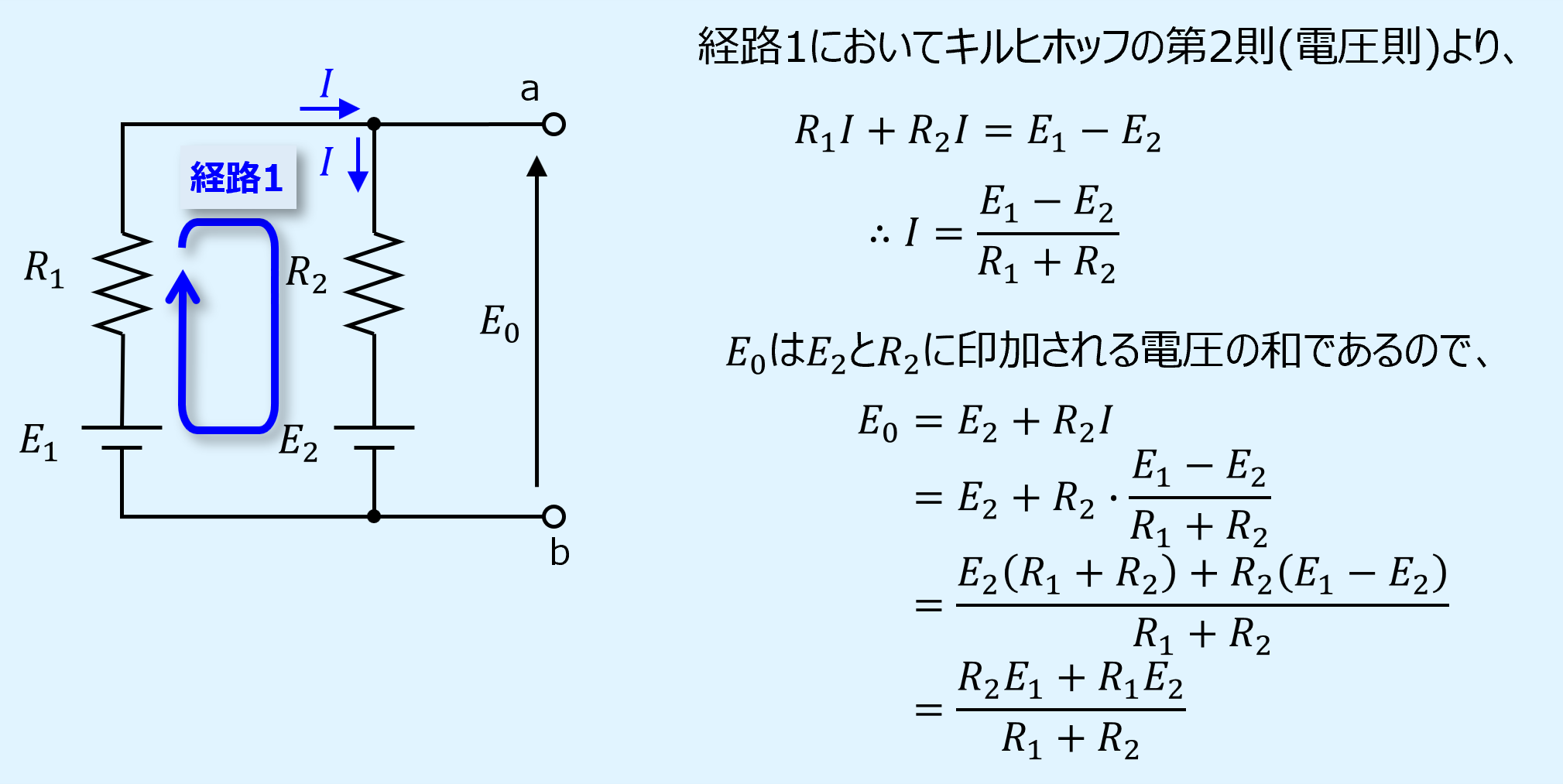
まず、キルヒホッフの法則を用いて開放電圧\(E_0\)を求めます。
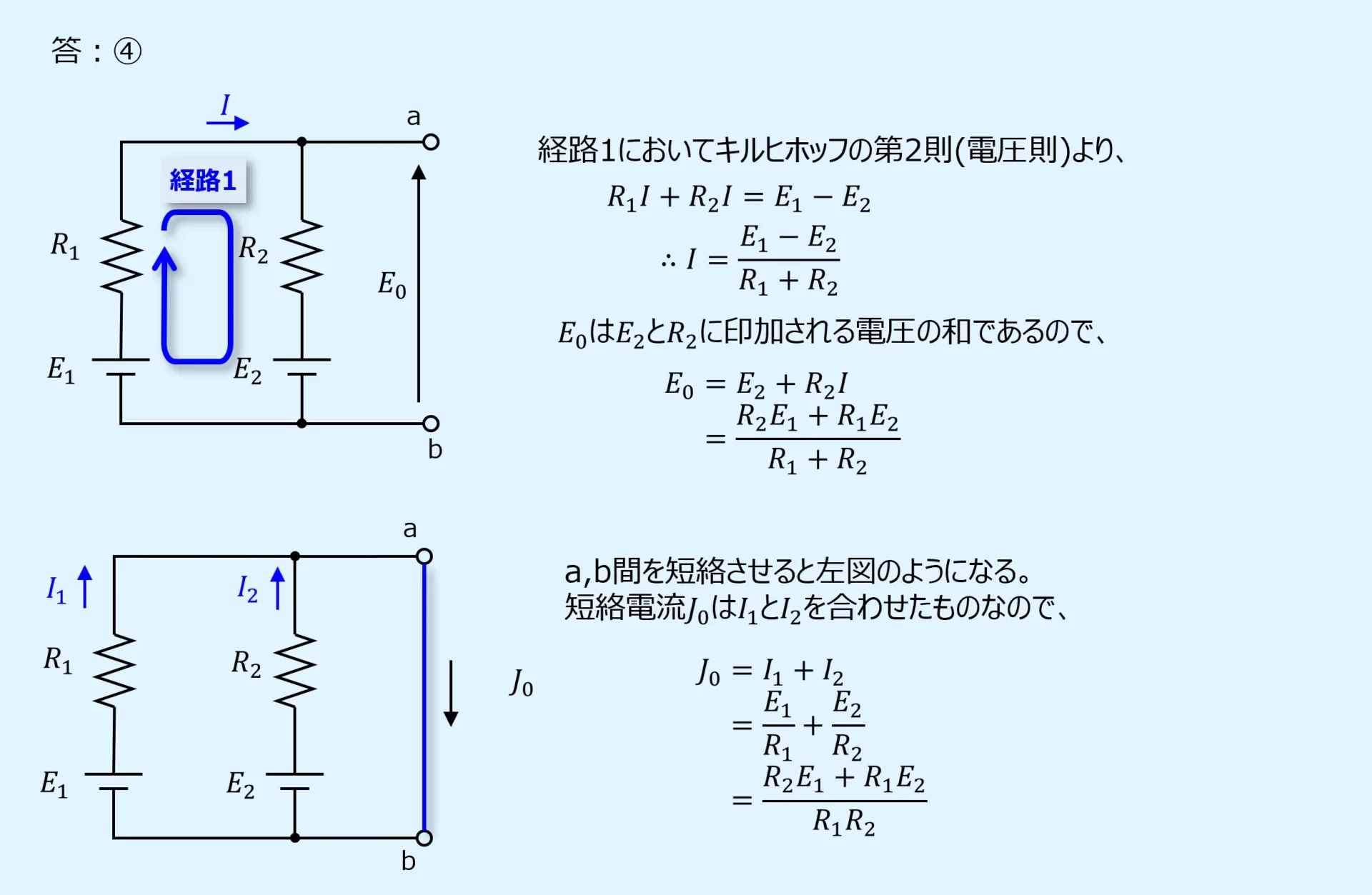
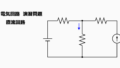
下図のように、経路1に関してキルヒホッフの第2法則を適用します。
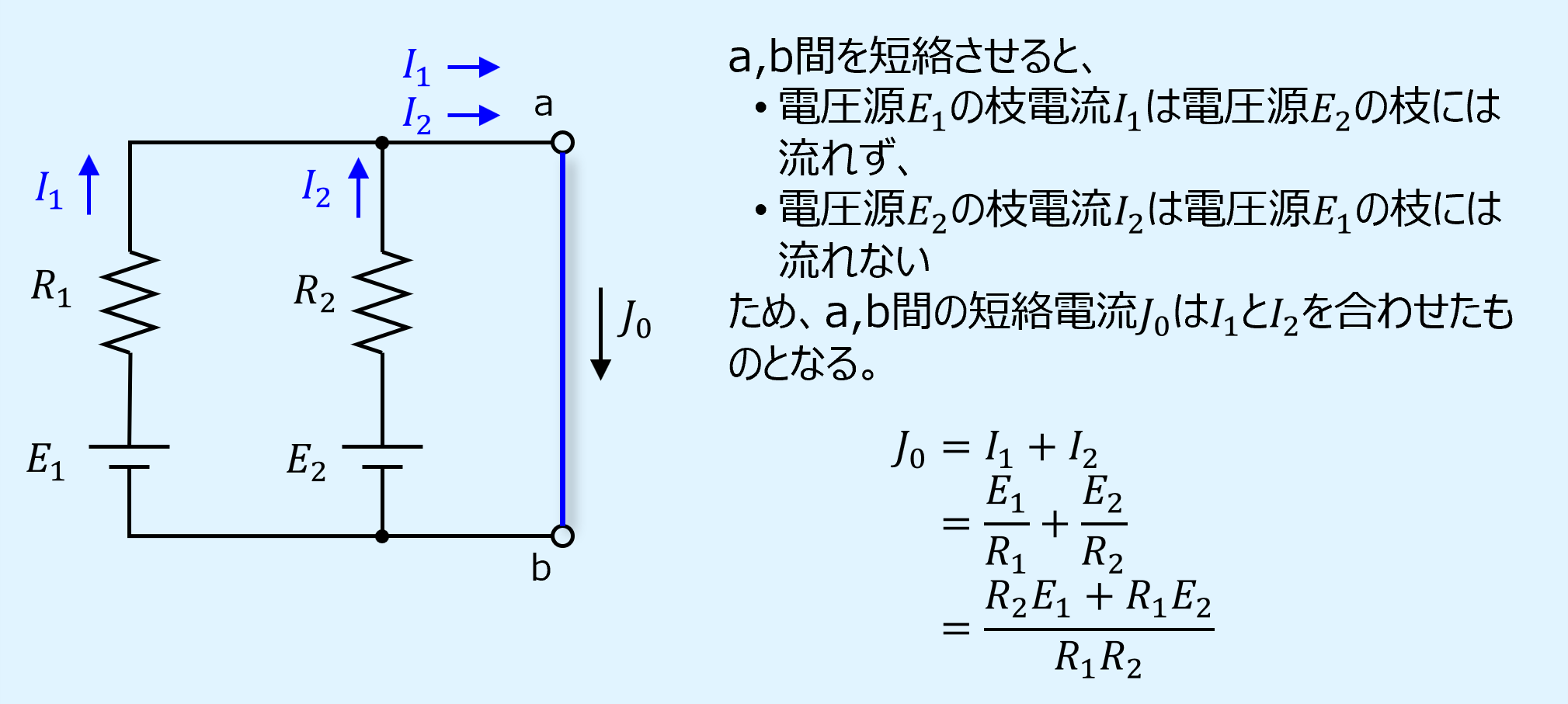
次に短絡電流\(I_0\)に関しては、電圧源\(E_1\)がある枝の枝電流\(I_1\)と電圧源\(E_2\)がある枝の枝電流\(I_2\)の和となります。
解法2:電圧源と電流源の相互変換
電圧源を電流源に変換、合成して開放端電圧を求め、その後、電流源を電圧源に変換して短絡電流を求める方法です。
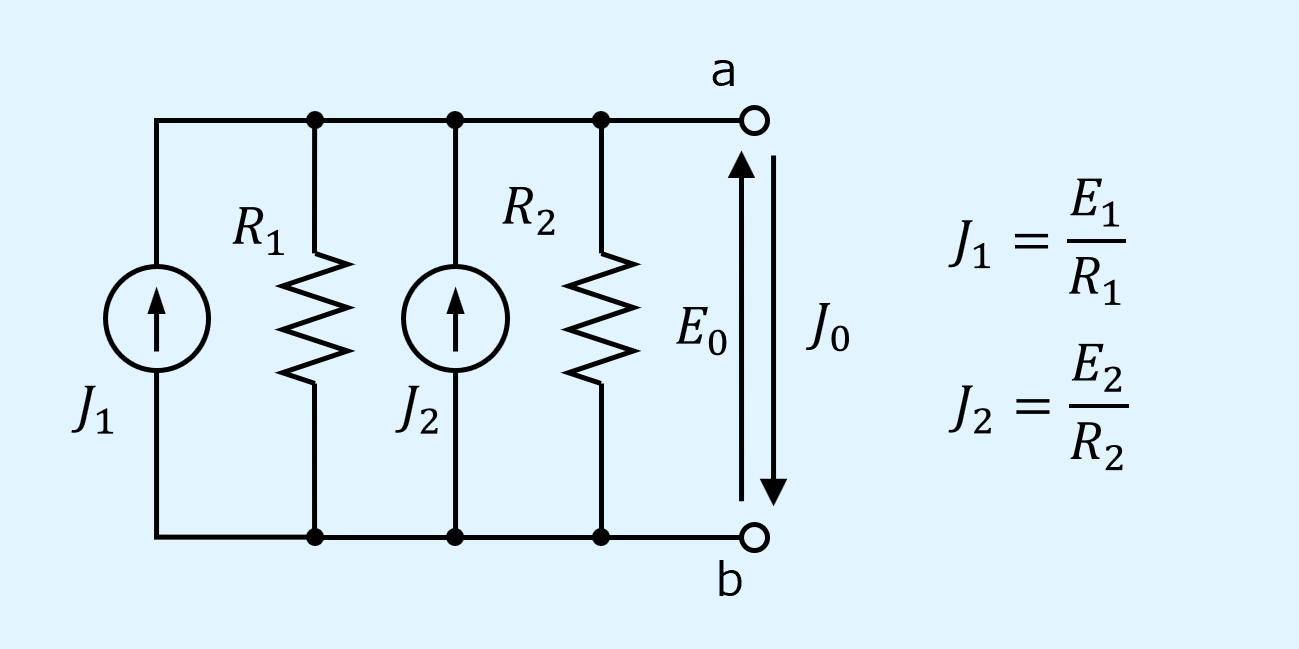
まず電圧源と抵抗の直列接続を電流源と抵抗の並列接続に変換します。
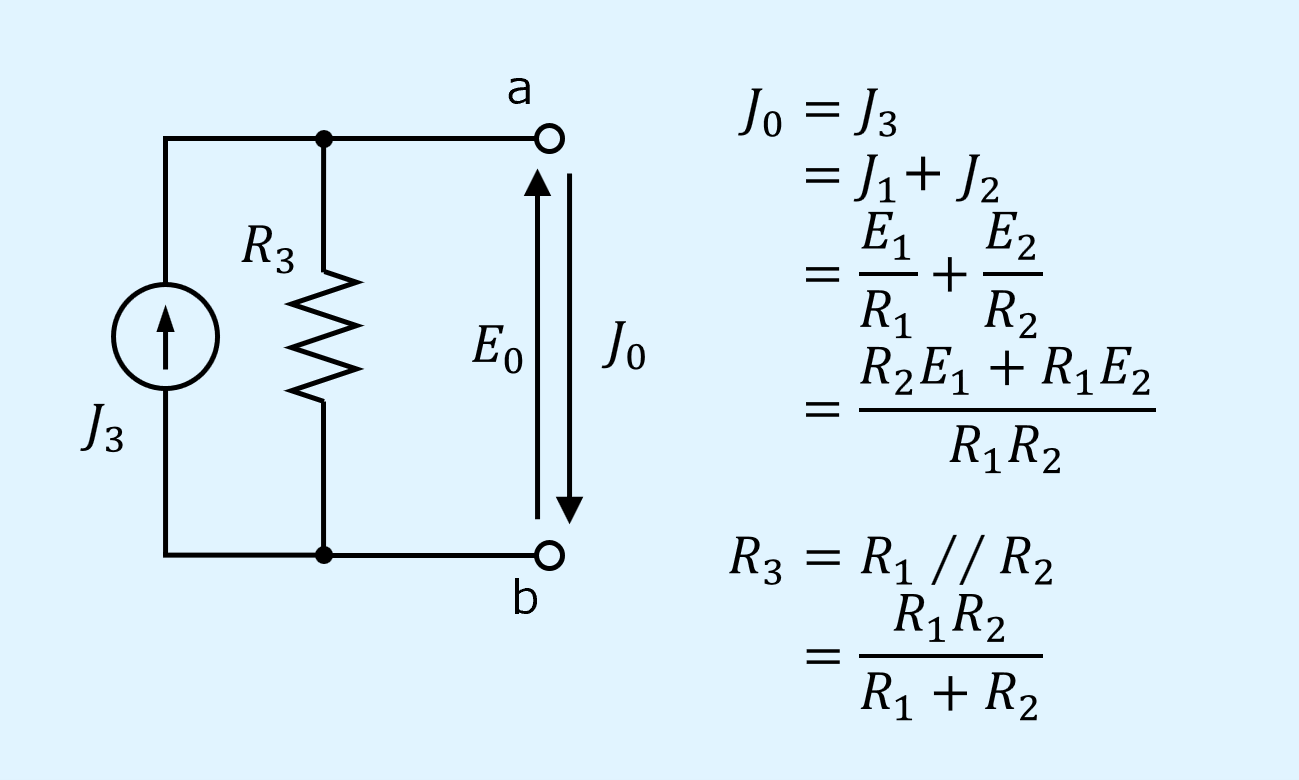
次に並列接続されている電流源と抵抗をそれぞれ合成します。
合成された\(J_3\)が短絡電流\(J_0\)です。
最後に電流源と抵抗の並列接続を電圧源と抵抗の直列接続に変換します。
この電圧源\(E_3\)が開放電圧\(E_0\)です。
演習問題1
電圧源2つと抵抗2つからなる直流回路で電圧と電流を求める問題を以下に示します。
ここでは先ほど説明したキルヒホッフの法則で解いた場合を掲載します。
その他
電気回路全般については以下をご覧下さい。
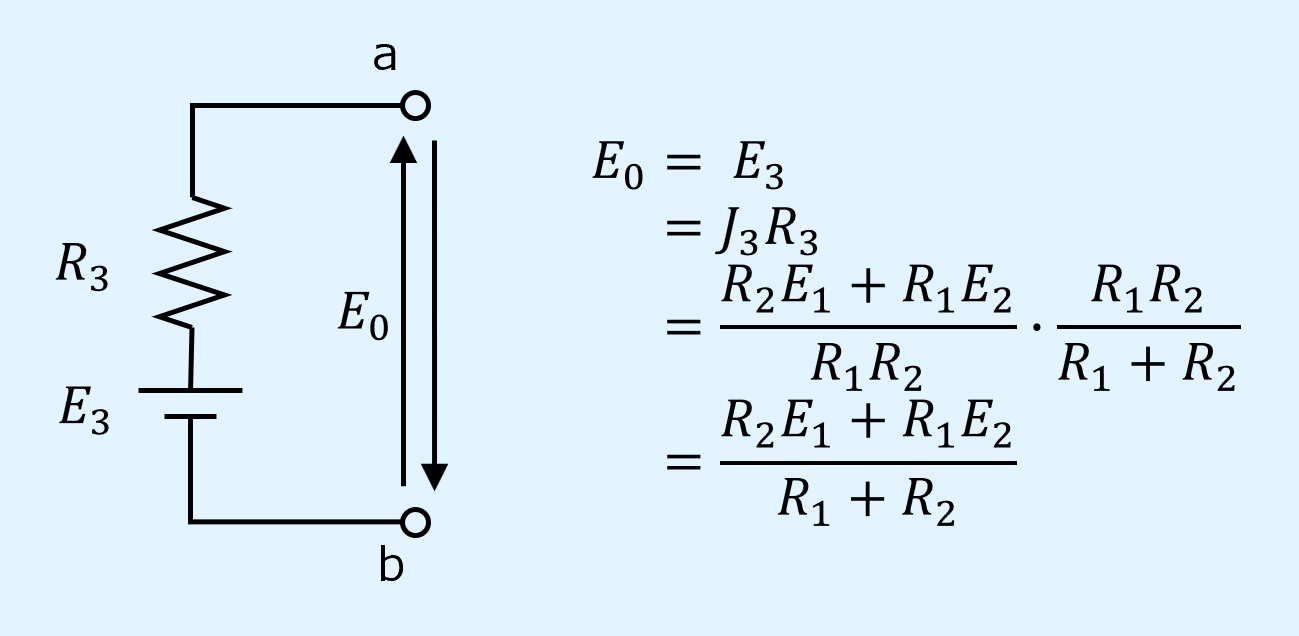

コメント