この記事では電気回路の一つである直流回路について、演習問題の解説をします。
電圧源2つと抵抗3つから成る単純な回路を取り扱います。
「演習問題 直流回路1」とは求める電流の位置が少し変わっており、電圧源の無い枝の電流を求めます。
解説用の回路
演習問題の前に、対象となる回路の解説を行います。
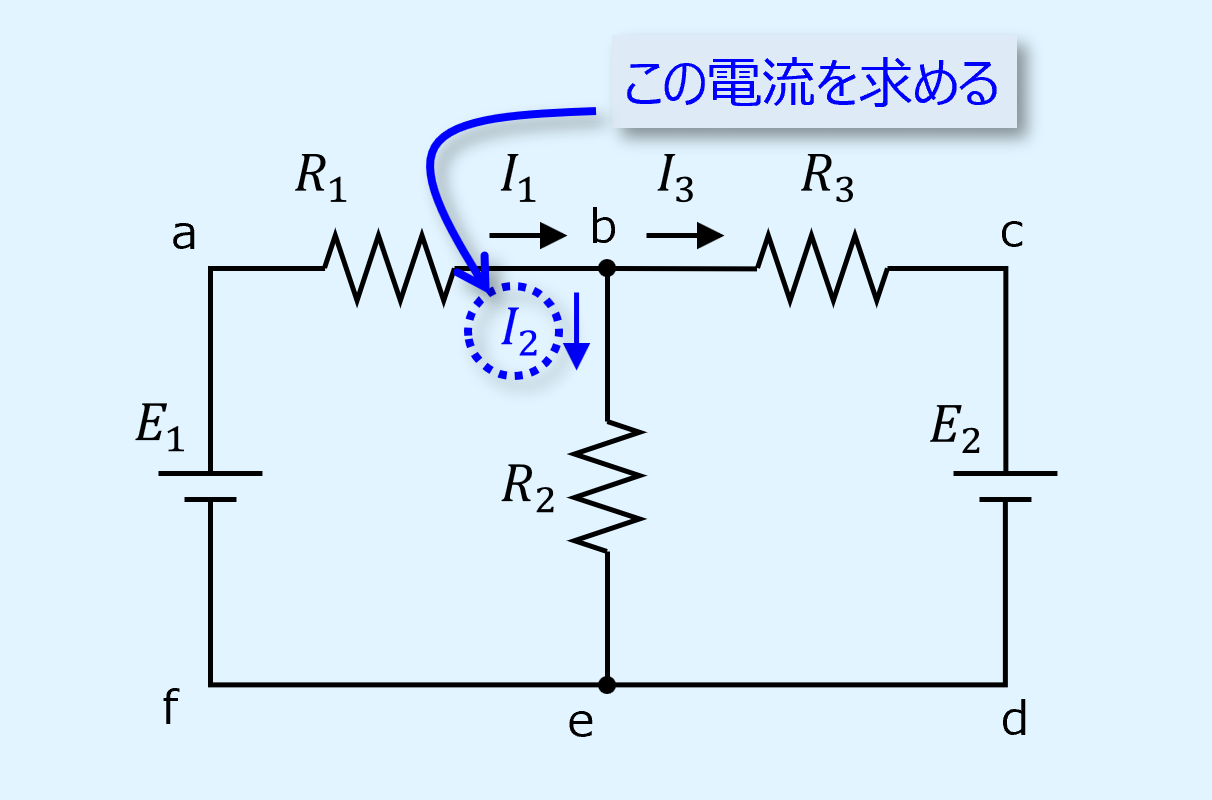
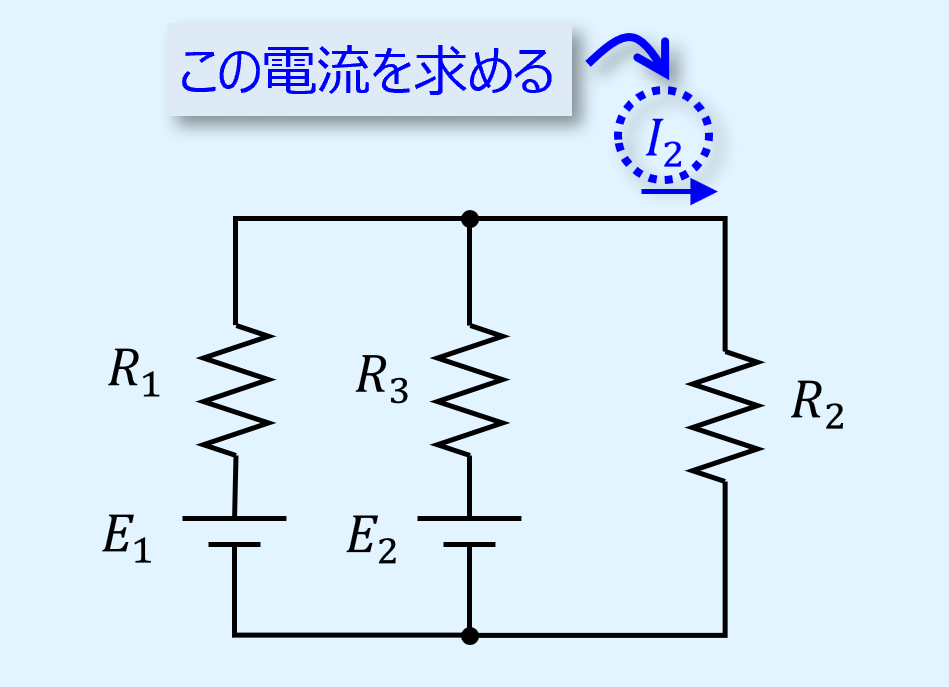
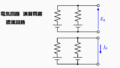
解説用の回路は以下となります。
電圧源2つ、抵抗3つから成る回路です。
ここで求めるのは\(R_2\)を含む枝に流れる電流\(I_2\)です。
\(I_3\)を求める場合は以下を参照してください。
電流\(I_2\)を求める解法は3つあり、枝電流法、重ね合せの理、電圧源と電流源の相互変換を用いる方法となります。
解法1:枝電流法
枝電流法はキルヒホッフの第1、2側を用いる方法です。
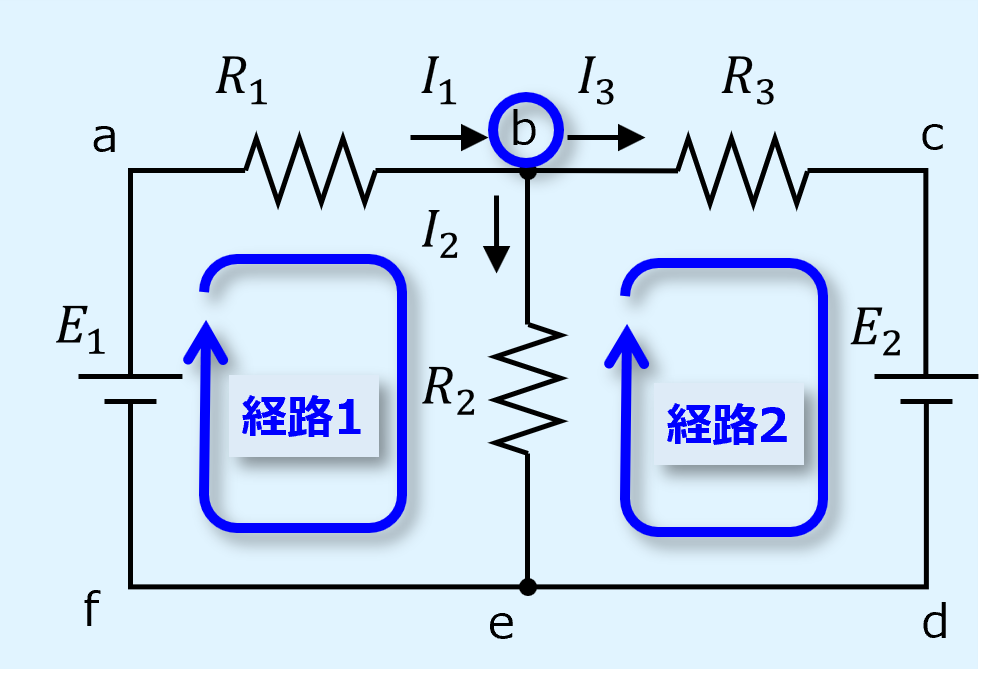
下図のように、独立した閉回路と独立した節点を選択し、式を立てます。
経路1、2と接点bに関して立てた式は以下の①~③となります。
ここから式変形を行い、\(I_2\)と\(I_3\)の連立方程式を導出します。
連立方程式の解法としては代入を行う方法と、クラメルの公式を用いる方法があります。
ここでは代入を行う方法で解を求めることにします。
解法2:重ね合せの理
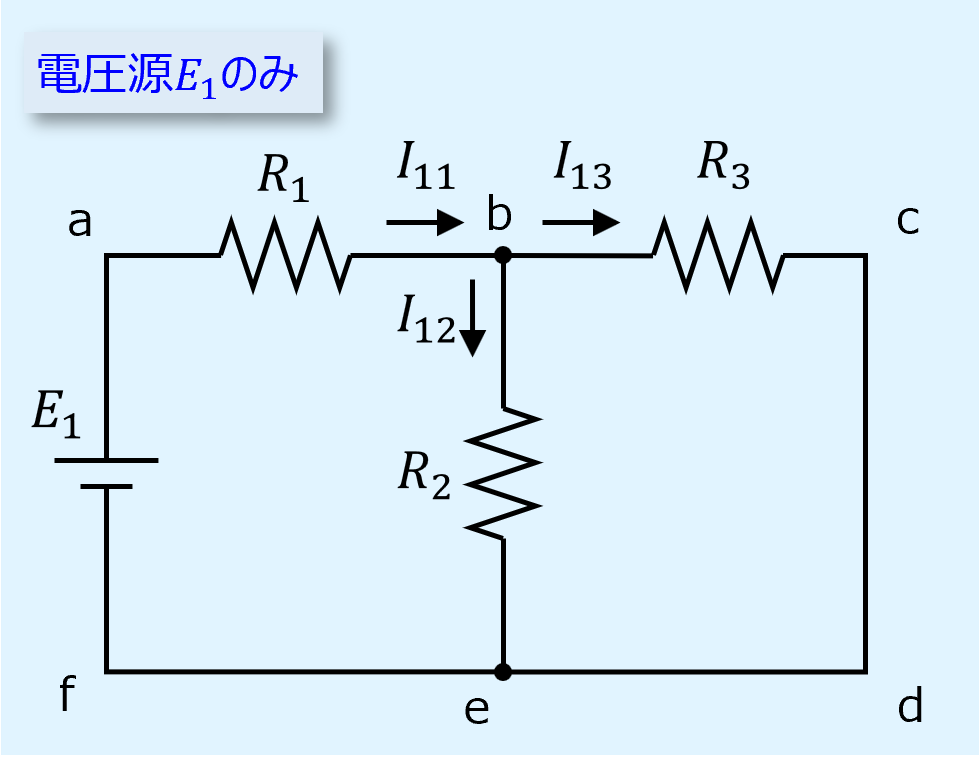
重ね合せの理を用いて、下図のように電圧源\(E_1\)のみの回路と電圧源\(E_2\)のみの回路に分けて解きます。
最初に電圧源\(E_1\)のみの回路について、\(I_{12}\)を求めます。
\(I_{12}\)はb,e間の電圧を抵抗比から求め、\(R_2\)で割ることで求められます。
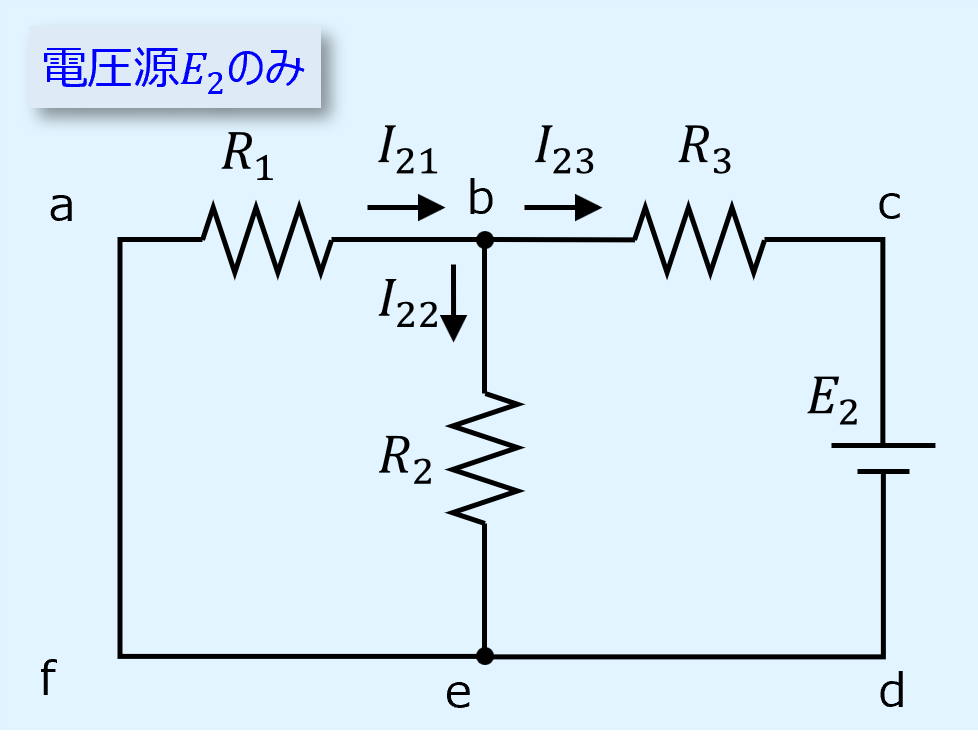
次に電圧源\(E_2\)のみの回路について、\(I_{22}\)を求めます。
電圧源\(E_1\)の場合と構成を比べると、抵抗と電圧源を入れ替えただけであるため、電流\(I_{22}\)は式①の抵抗と電圧源を入れ替えたものとなります。
電圧源\(E_1\)のみの場合の電流\(I_{12}\)と電圧源\(E_2\)のみの場合の電流\(I_{22}\)を合わせると、元の回路の電流\(I_2\)となります。
結果は枝電流法と同じになります。
解法3:電圧源と電流源の相互変換
このケースでは求めたい電流が流れている枝に電源が無いため、電圧源と電流源の相互変換で解くことができます。
電圧源と電流源の相互変換を行って解くに当たり、分かりやすくするために下図のように回路要素の配置を整理します。
右端に求めたい電流が流れる枝をもってきています。
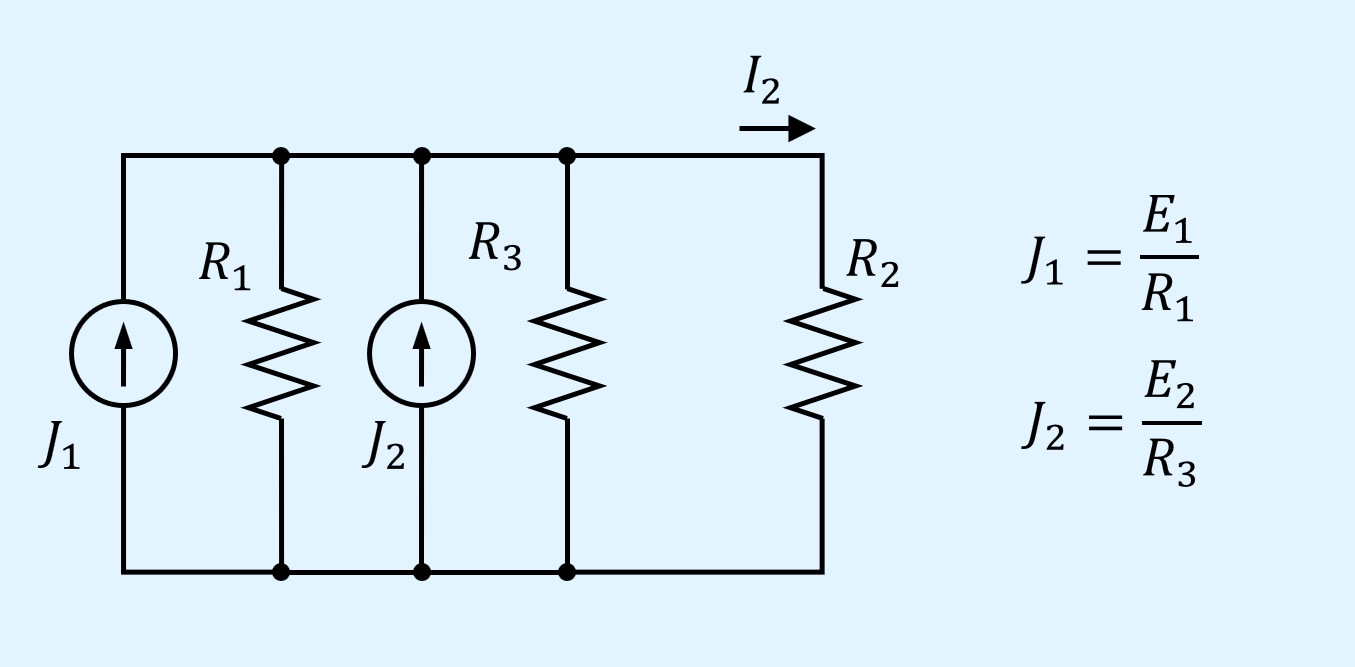
最初に電圧源と抵抗が直列接続している個所を、電流源と抵抗の並列接続に変換します。
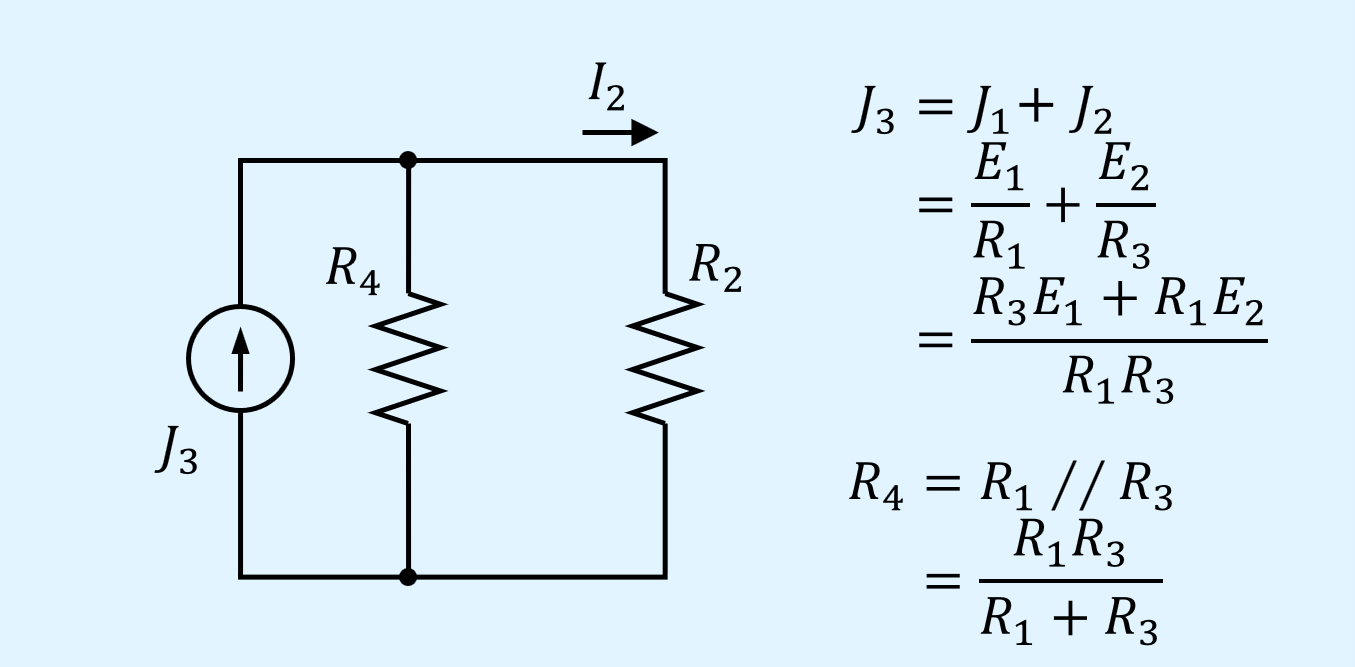
次に並列接続している電流源と抵抗をそれぞれ合成します。
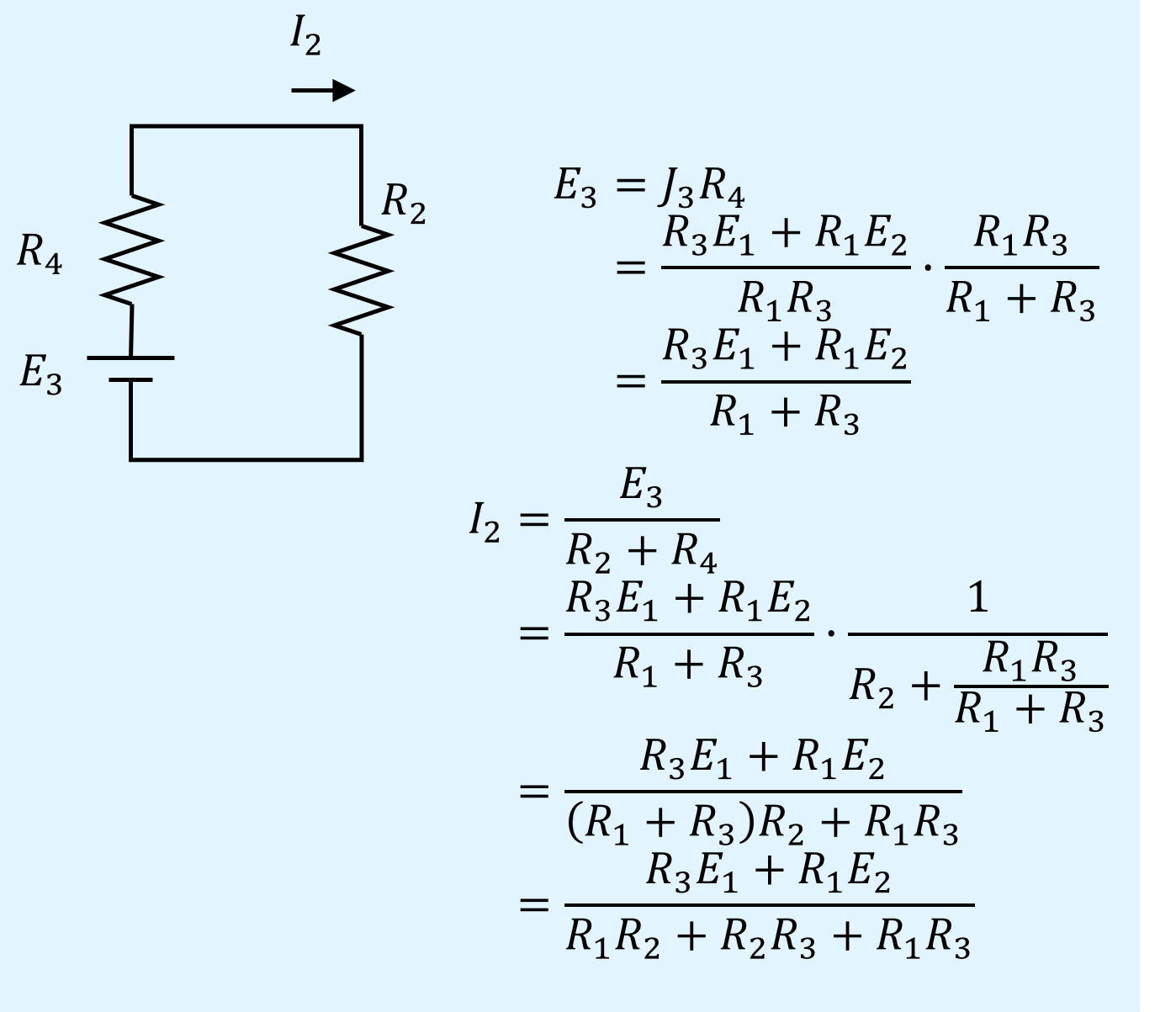
最後に電流源と抵抗の並列接続を電圧源と抵抗の直列接続に変換し、\(R_2\)も含めて電流\(I_2\)を求めます。
結果は枝電流法と同じになります。
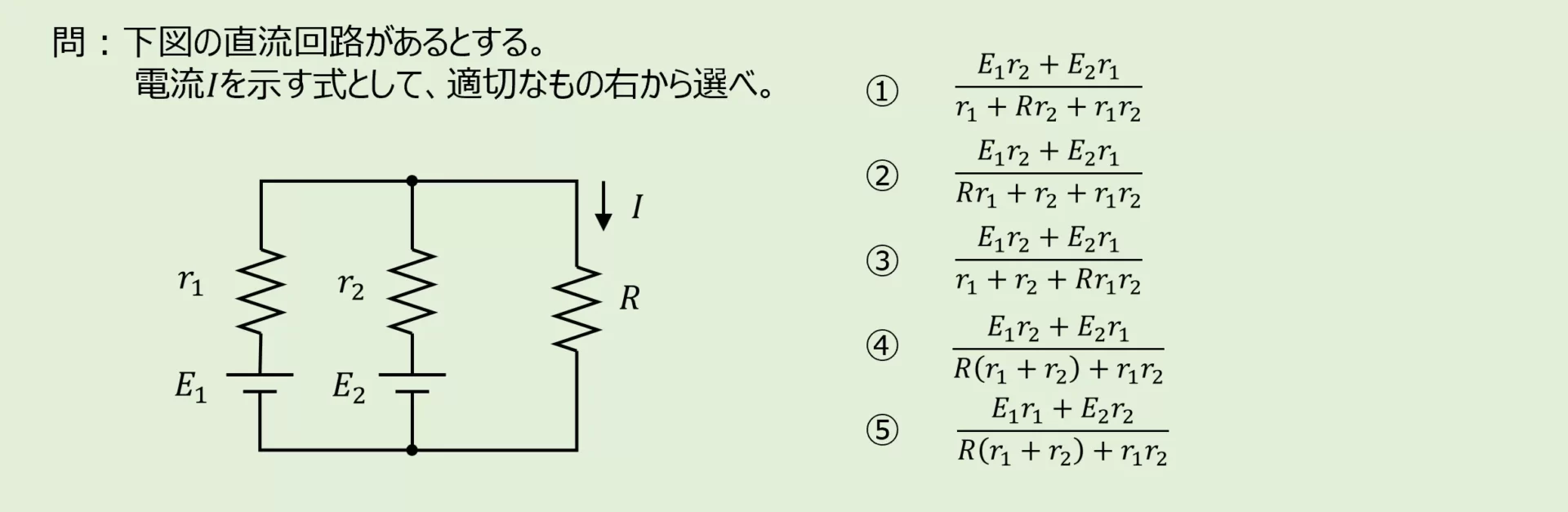
演習問題1
電圧源2つ,抵抗3つから成る直流回路のおいて、電圧源の無い枝の電流を求める例題を以下に示します。
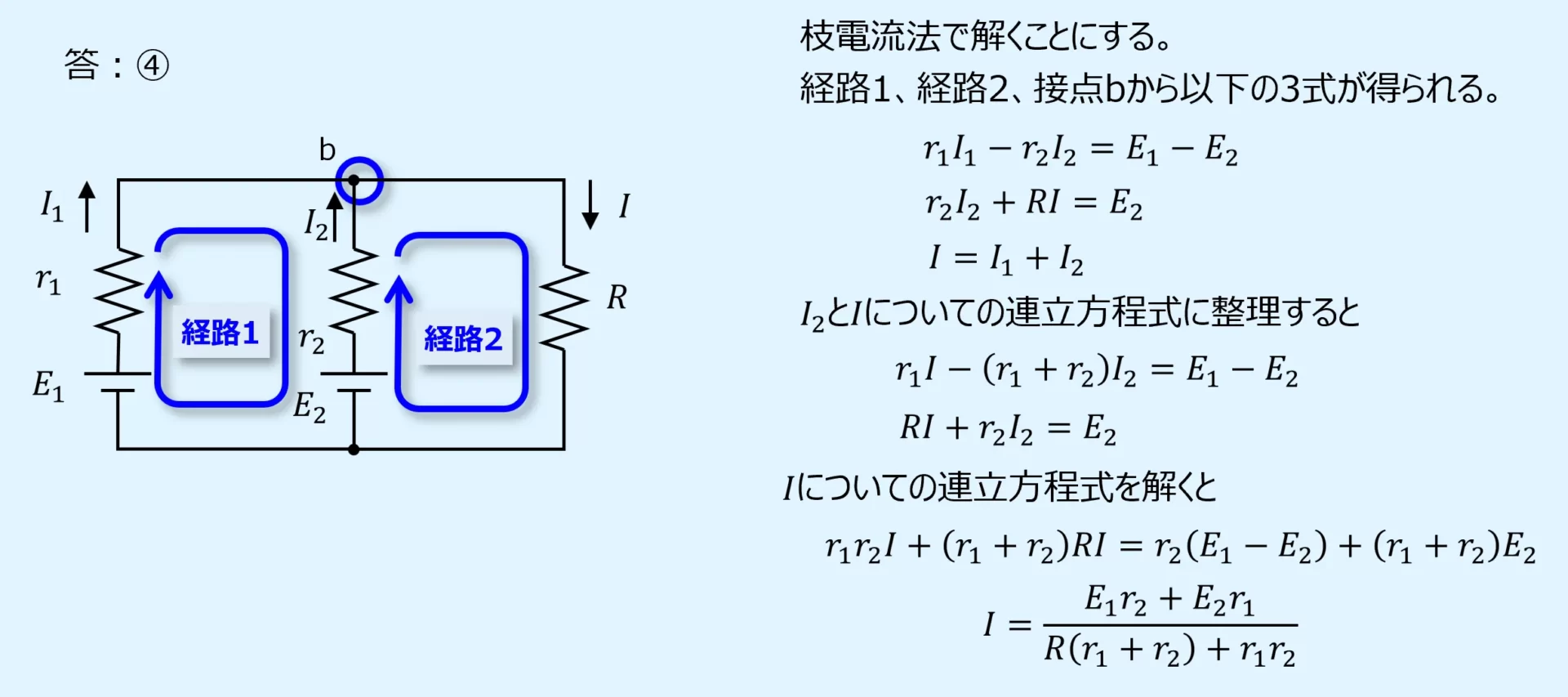
ここでは先ほど説明した枝電流法で解いた場合を掲載します。
その他
電気回路全般については以下をご覧下さい。
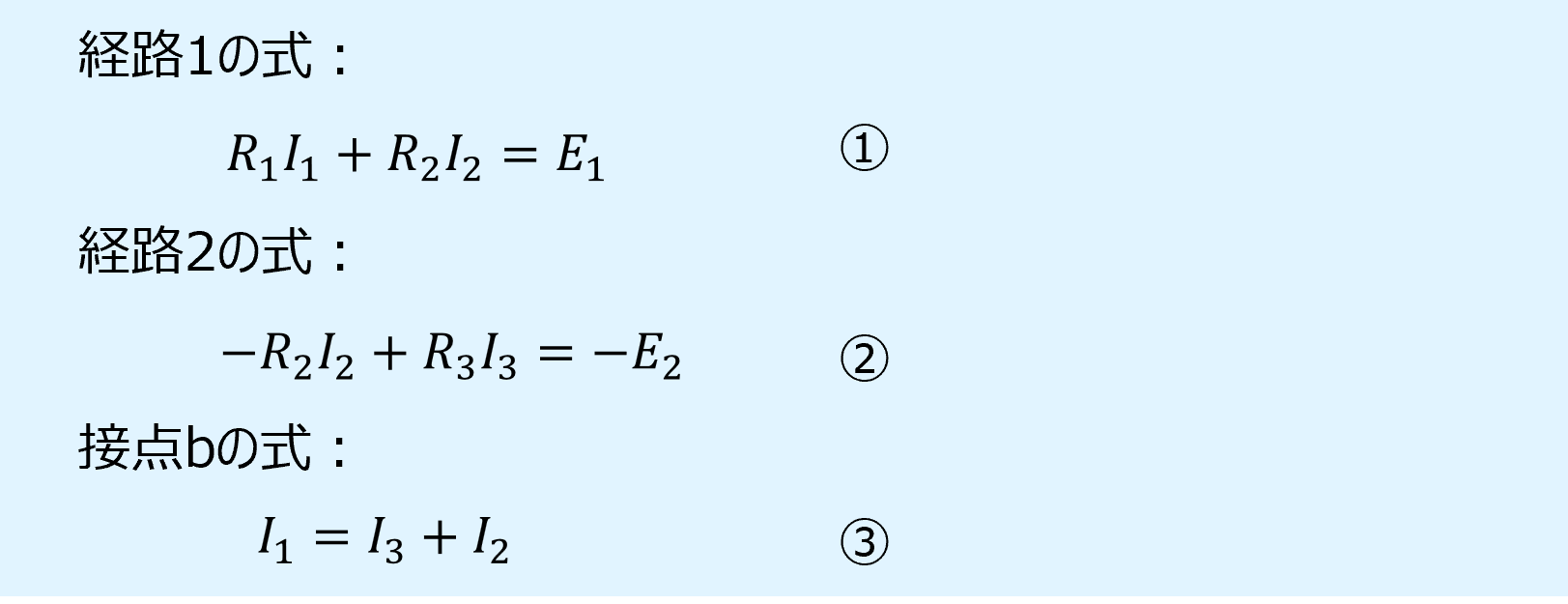




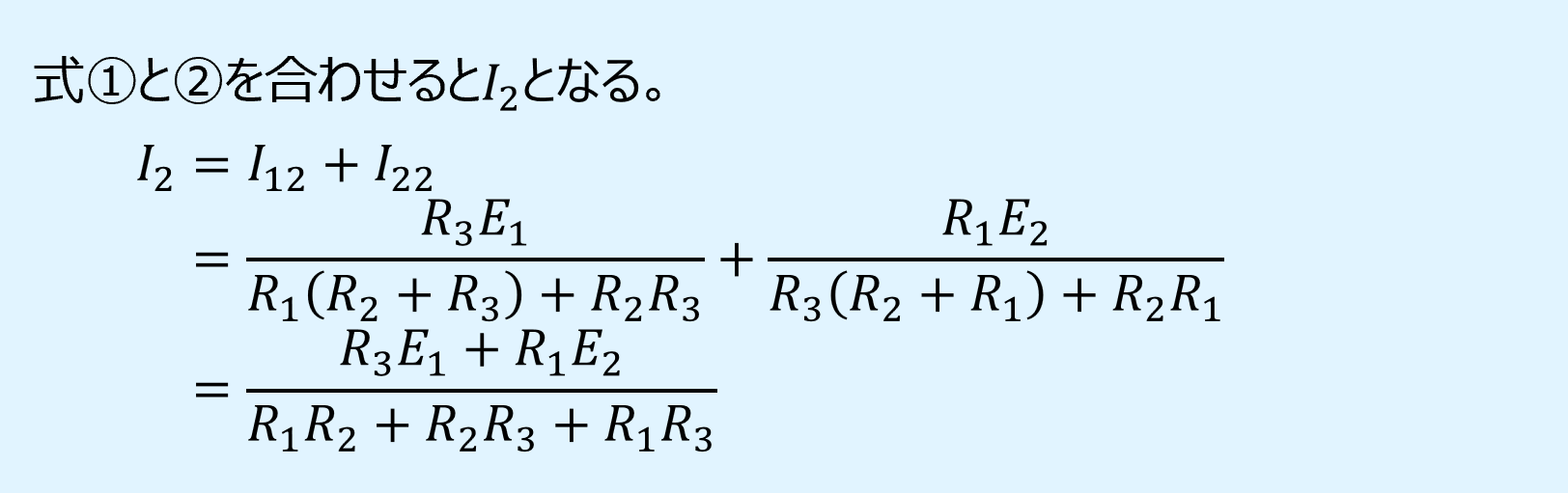
コメント