重ね合せの理

【まとめ】重ね合せの理

重ね合せの理の概要

重ね合せの理(Low of Superposition)は電流に関する定理です。
重ねの定理、重ねの理とも呼びます。
電気回路中に複数の電源がある場合の計算を容易にします。

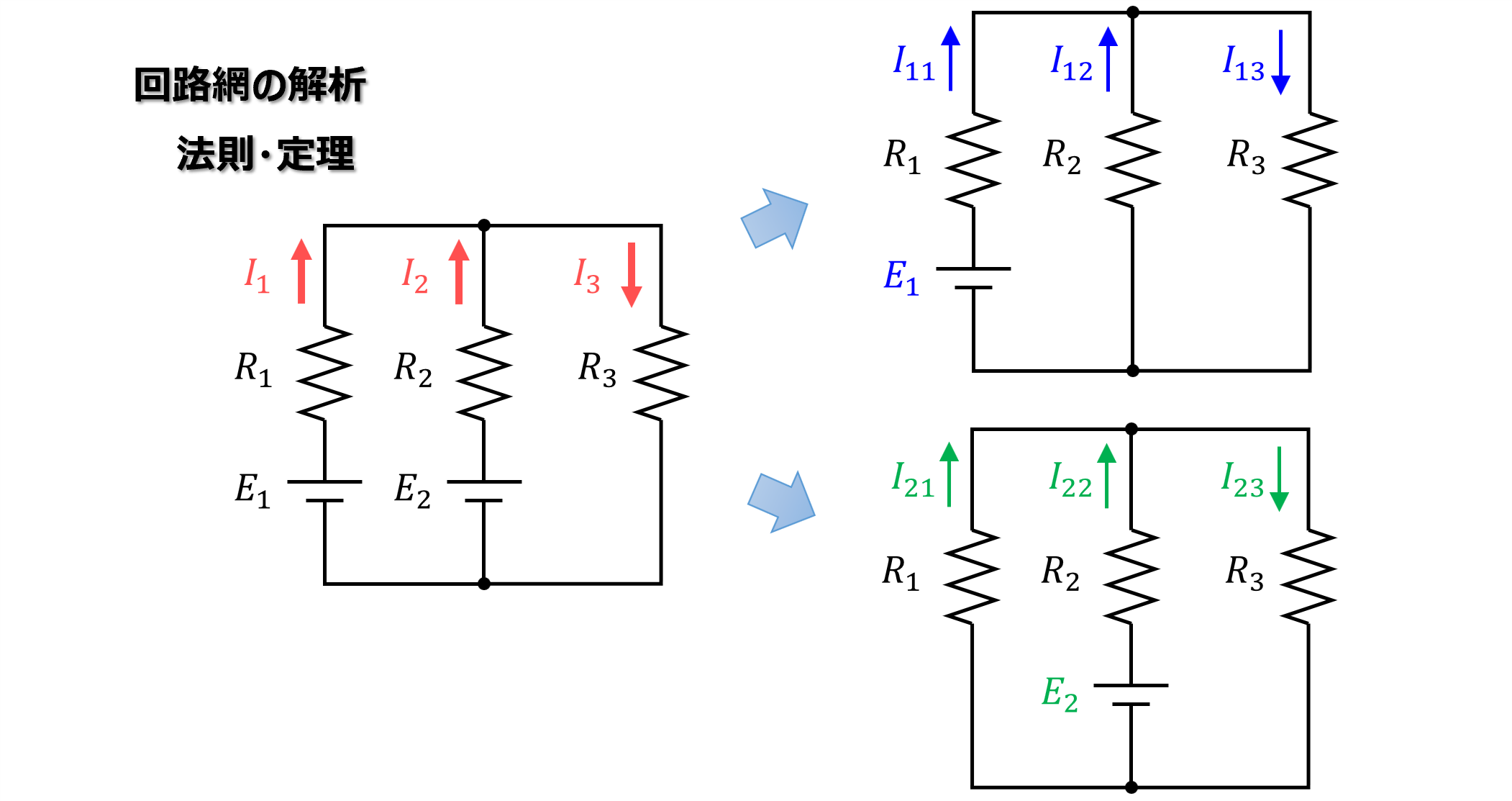
複数ある電源のうちの一つを選択し、それ以外の電源は無視をして回路内の電流を計算します。
次に別の電源を選択し、同様にそれ以外は無視をして回路内の電流を計算します。
これを電源の数だけ繰返します。
最後に各電流について、各計算結果を合算する、すなわち重ね合せると元の回路の電流値が求められます。
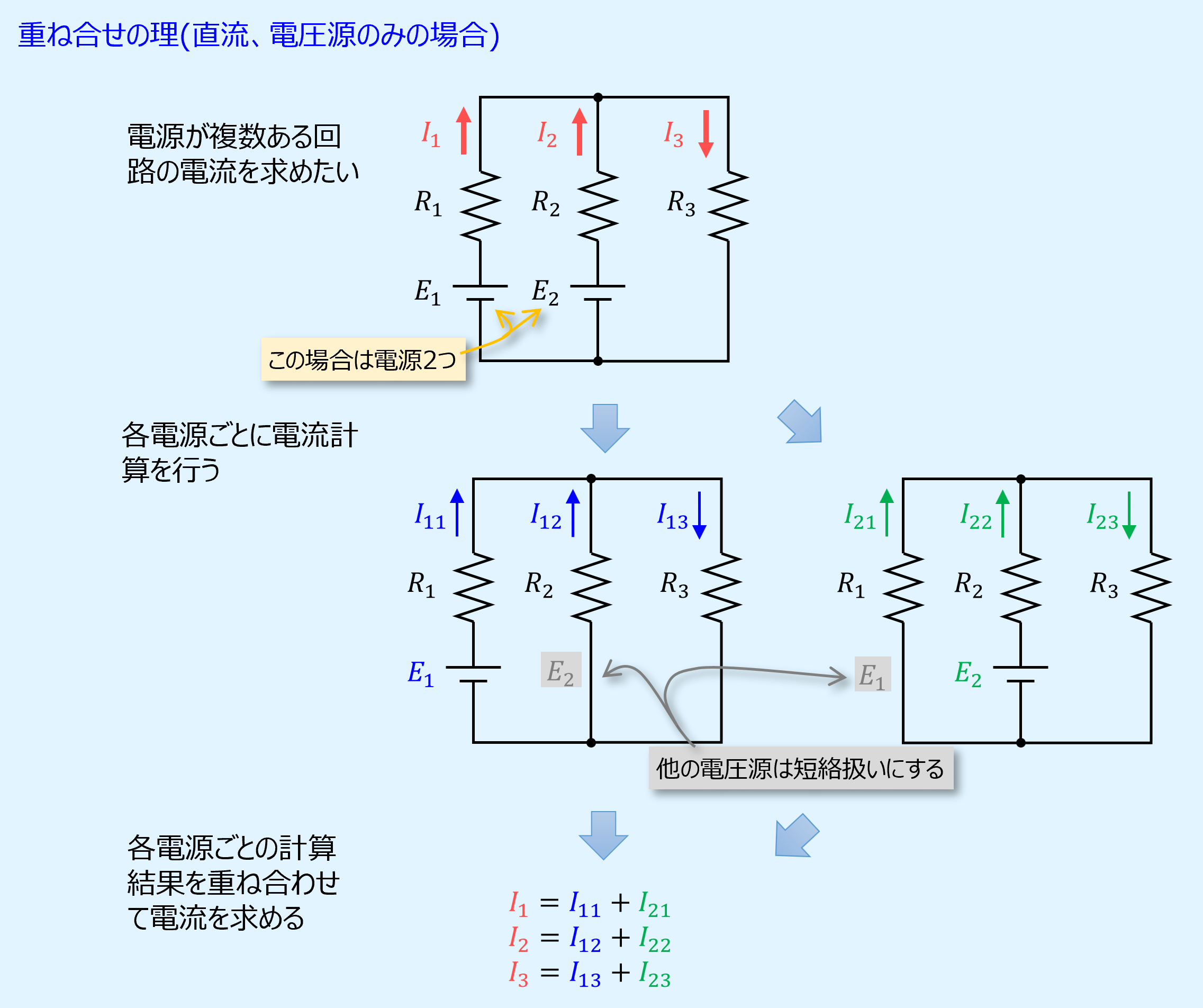
また、「電源を無視して」と述べましたが、正確には電圧源は短絡しているものとして扱います。

複数の電源を有する回路は、キルヒホッフの法則を用いて計算式を立てることで解くことが可能ですが、閉回路の選択によっては上手く解けない場合もあります。
これに対し重ね合せの理では、分離させた各回路の電源が1つであるため、合成抵抗計算とオームの法則のみで楽に求められます。

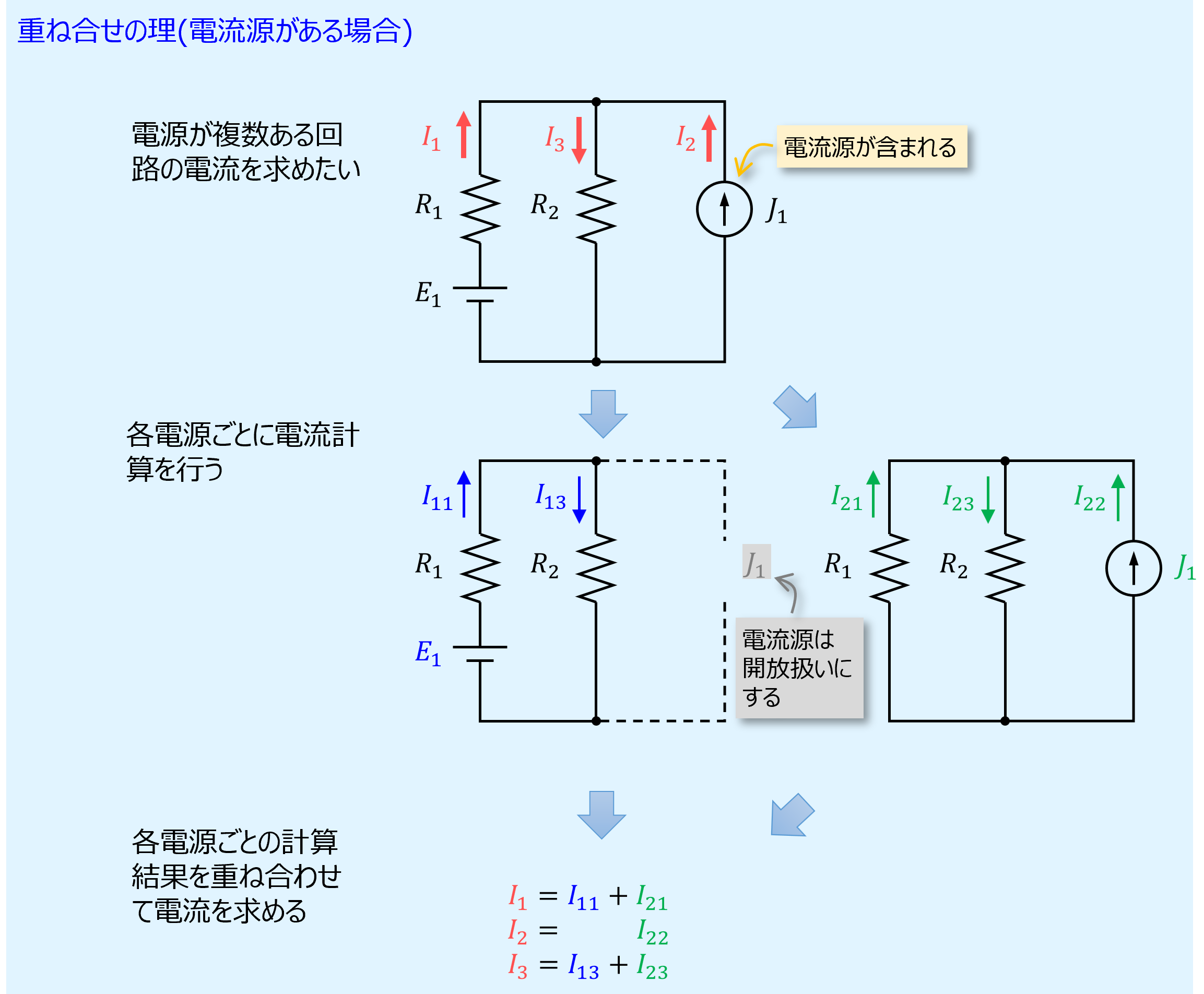
電流源がある場合

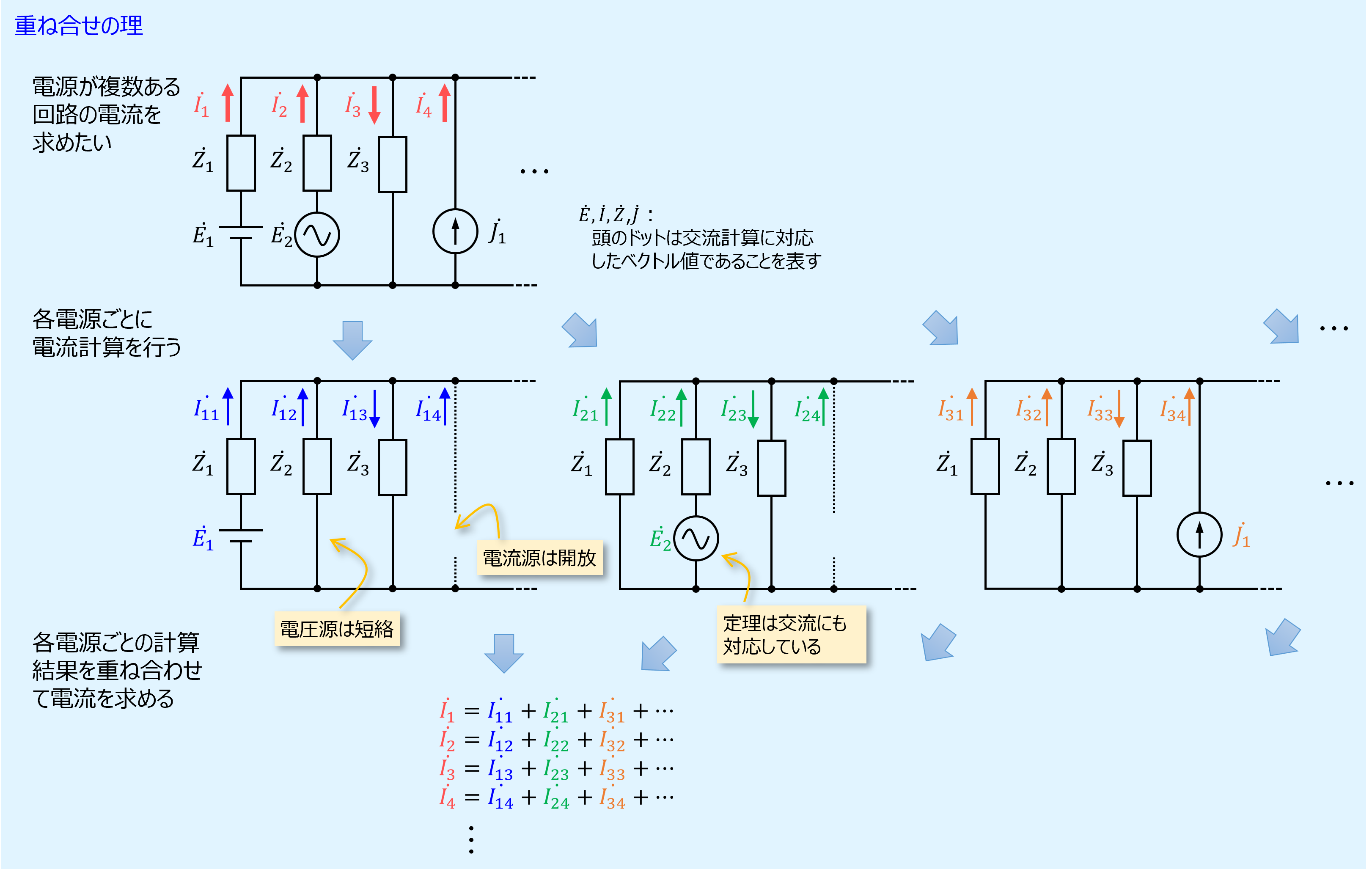
除外する電源が電圧源の場合は短絡扱いとしますが、電流源である場合は開放端として扱います。

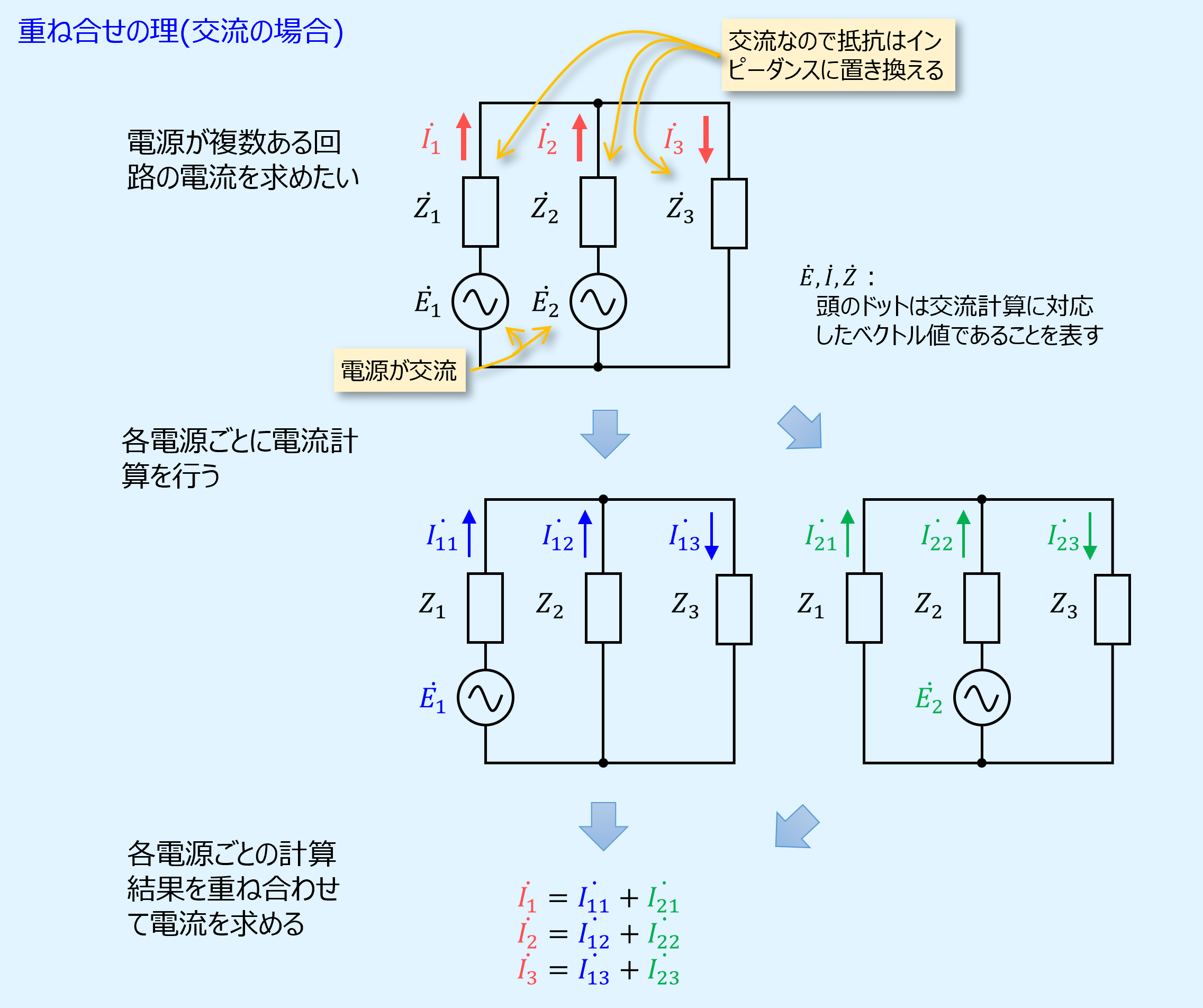
交流でも成り立つ

重ね合せの理は交流の場合でも成り立ちます。
電圧源に交流が含まれると互いの位相関係を考える必要がありますが、重ね合せの理を用いると単一電源で扱うことができます。