この記事では電気回路で生じる共振について説明をします。
RLC直列回路のインピーダンスと電流の振幅、位相の周波数特性との関係も含めています。
【まとめ】回路の共振
RLC直列回路と電流
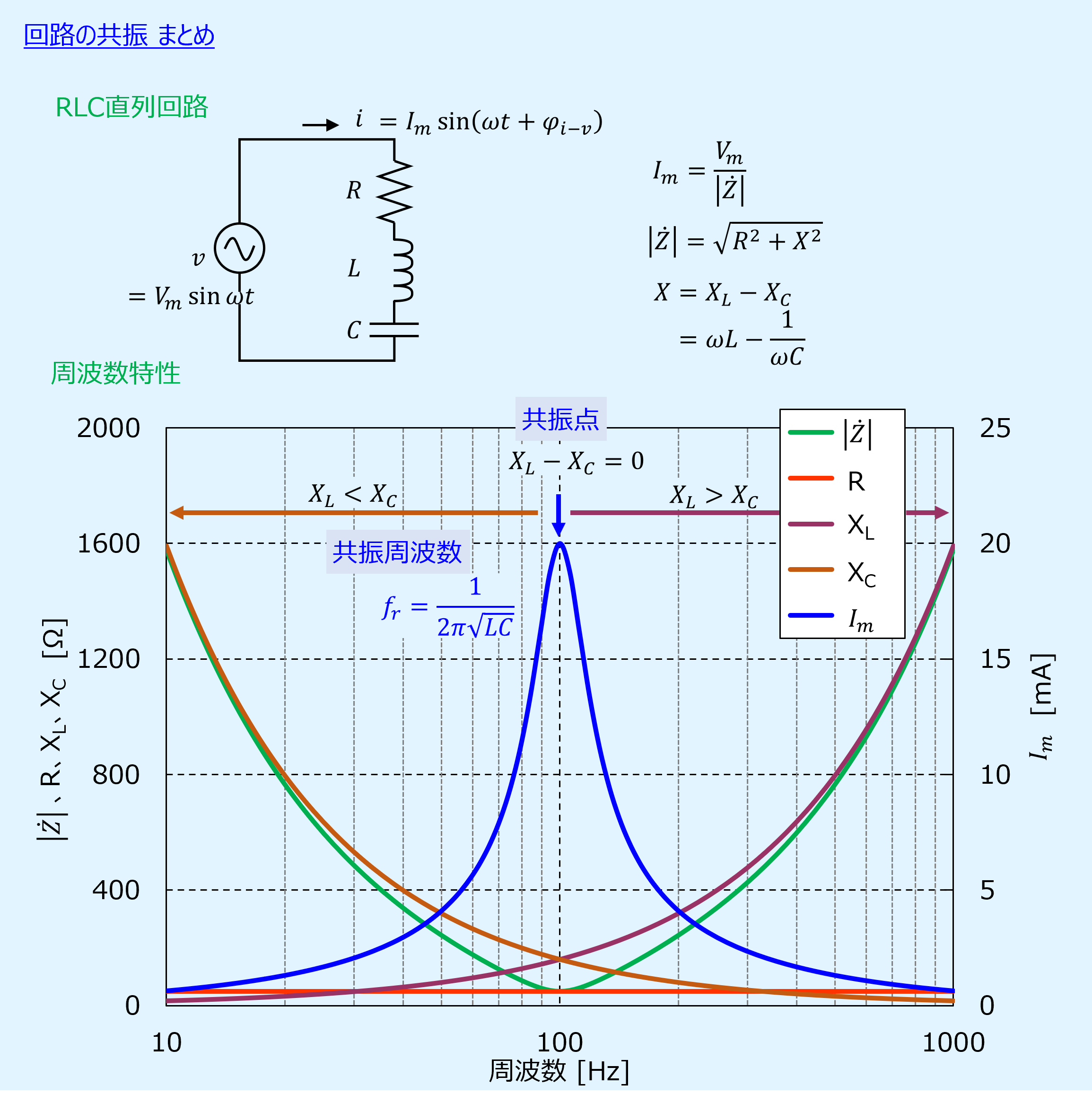
以下にRLC直列回路と電流の関係を示します。
別の記事で電流を基準として電圧を出しましたが、ここでは電圧と電流の関係を入れ替えて示しています。
ここで、交流での抵抗を表すリアクタンス\(X_L\)と\(X_C\)は周波数によって値が変化します。
そのため、リアクタンス\(X\)と抵抗\(R\)と合成したインピーダンス\(\dot{Z}\)、及び電圧\(\dot{V}\)をインピーダンス\(\dot{Z}\)で割った電流\(\dot{I}\)の最大振幅\(I_m\)、電圧と電流の位相差\(\varphi_{i-v})も周波数によって値が変わります。
本記事ではインピーダンスの大きさ\(|\dot{Z}|\)と電流の最大振幅\(I_m\)、電圧と電流の位相差\(\varphi_{i-v})が周波数によってどのように変化するのか、また変化させる途中で起きる事象について説明します。
抵抗とリアクタンスの周波数特性
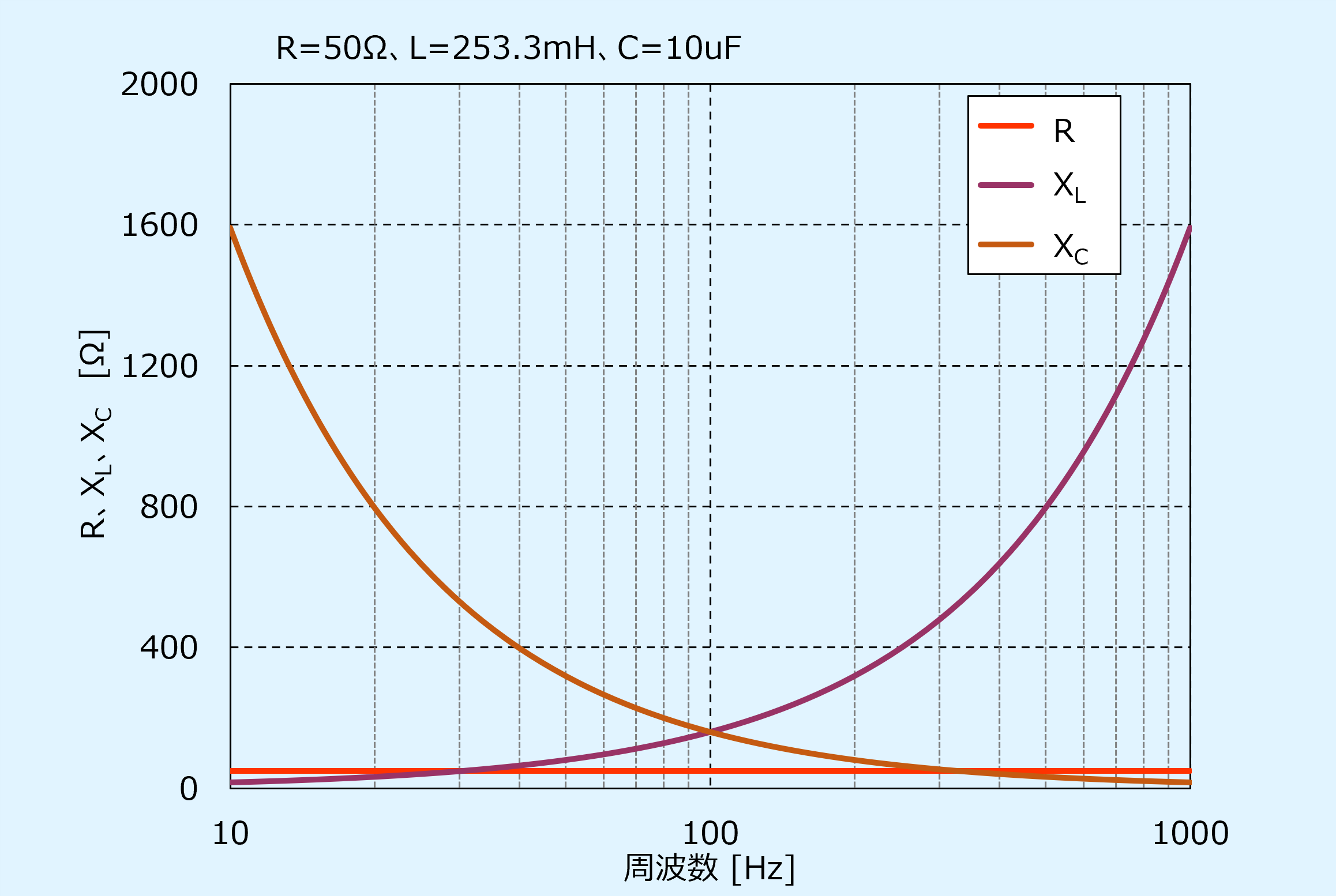
最初に抵抗\(R\)、誘導性リアクタンス\(X_L\)、容量性リアクタンス\(X_C\)について、周波数を変化させたときにどうなるのかを以下に示します。
横軸に周波数を取り、縦軸に\(R\)、 \(X_L\)、 \(X_C\)の値を示しています。
これを周波数特性と呼びます。
条件としては、\(R=50\)Ω、\(L=253.3\)mH、\(C=10\)uFの場合で、周波数は10Hzから1000Hzまで変化させています。
横軸は対数表示にしています。
抵抗\(R\)は周波数特性を持たないので、周波数によらず一定です。
誘導性リアクタンス \(X_L\)は周波数が低いと小さく、周波数が高くなるにつれて大きくなります。
逆に容量性リアクタンス\(X_C\)は周波数が小さいと大きく、周波数が高くなるにつれて小さくなります。
インピーダンスと電流の周波数特性
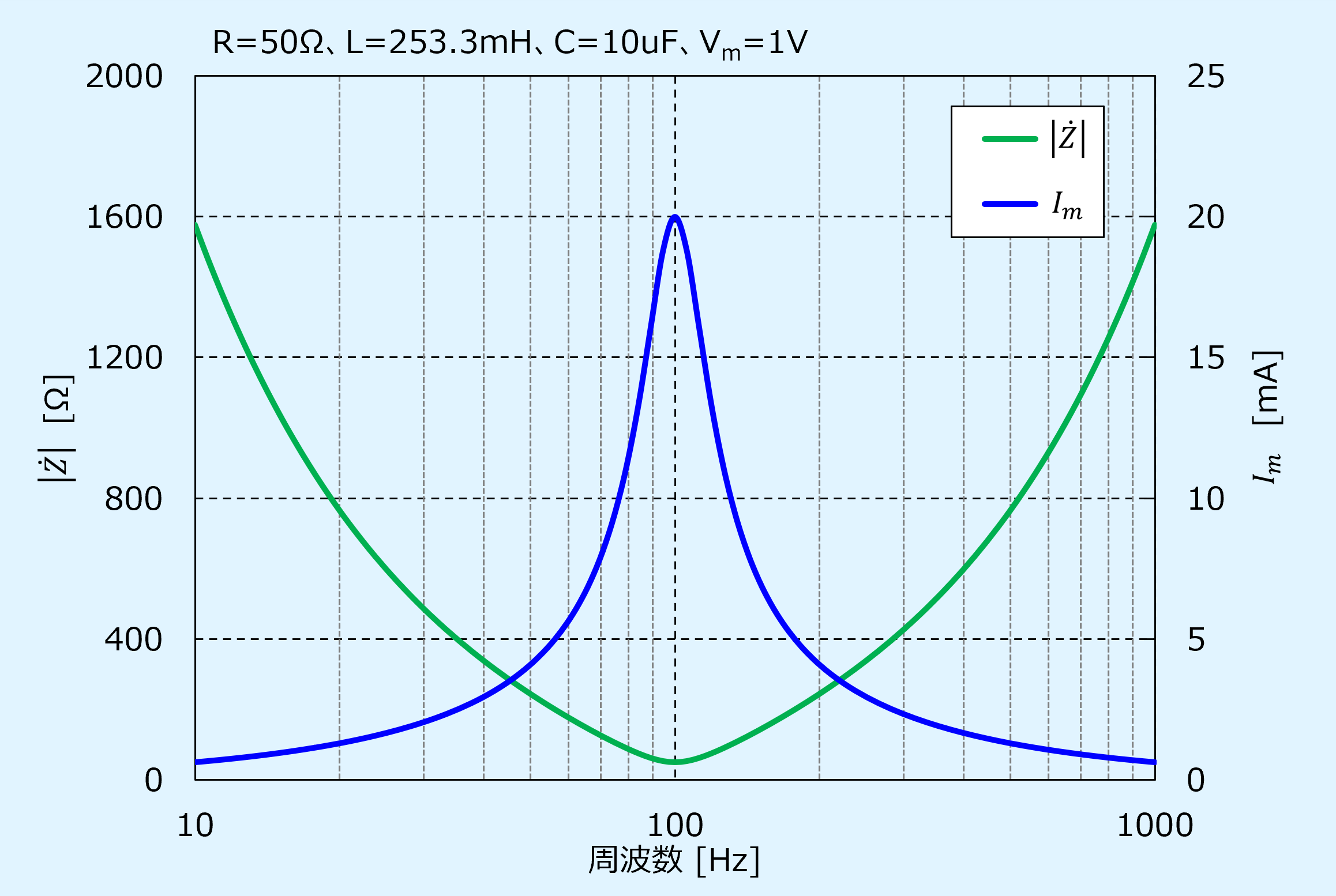
次にインピーダンスの大きさ\(|\dot{Z}|\)と電流の最大振幅\(I_m\)の周波数特性を示します。
電圧の最大振幅\(V_m\)は1Vとしています。
また、左側の縦軸がインピーダンスの大きさ、右側の縦軸が電流の最大振幅となっています。
抵抗、誘導性/容量性リアクタンスを合成したインピーダンスの周波数特定はV字の形となります。
周波数が低い領域では容量性リアクタンスの影響が強く出てインピーダンスは大きく、周波数が高くなるにつれて小さくなります。
そして、ある周波数で誘導性/容量性リアクタンスが打ち消し合い抵抗のみとなる最小値を迎えます。
その後の周波数が高い領域では誘導性リアクタンスの影響が強く出てインピーダンスは大きくなっていきます。
電流は電圧をインピーダンスで割ったものですので、電圧が一定の場合、ここでは1Vとしていますが、電流はインピーダンスとは逆の周波数特性となります。
電流は低域で小さく、周波数が高くなるに従い大きくなり、ある点で最大値を迎え、その後は周波数が高くなるに従い小さくなります。
共振
対象の構造に由来するある特定の周波数において、出力が大きくなる現象を共振(resonance)といいます。
RLC直列回路の周波数特性で電流が最大となる点も共振であり、直列共振(series resonance)いいます。
また、LCが直列に接続された回路のことを直列共振回路と呼びます。
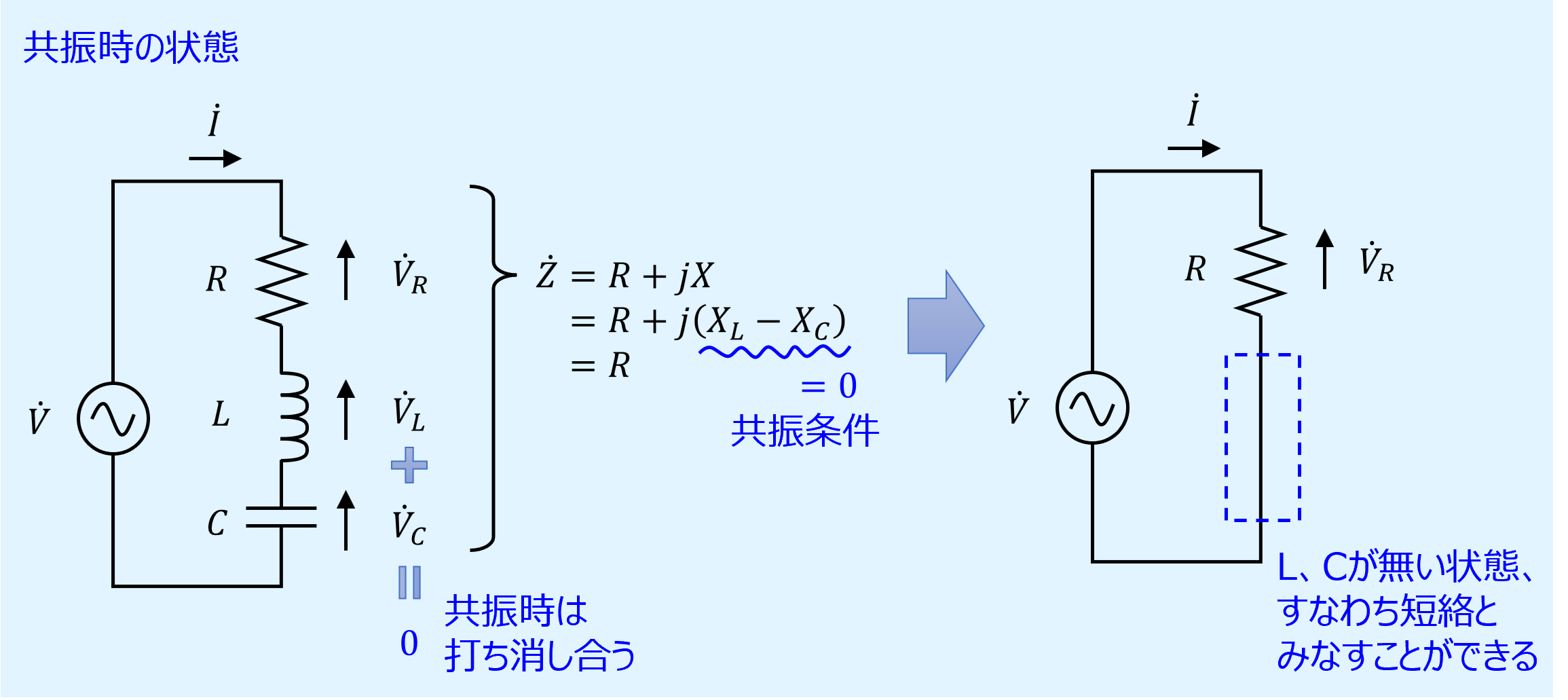
共振点ではインダクタンス\(L\)とキャパシタンス\(C\)に生じる電圧が互いに打ち消し合っており、実質的に\(L\)、\(C\)が無い状態、すなわち短絡状態にあるとみなすことができます。
また、抵抗が無い場合は、インピーダンスが0となり、電流が∞となりますが、それは理論上の話であり、実際はインダクタンスに必ず抵抗成分が含まれているため、インピーダンスが0となることはありません。
共振となる条件、及び共振周波数は以下の通りです。
インダクタンス\(L\)とキャパシタンス\(C\)の値を変えたときに、共振周波数がどうなるのかを以下に示します。
インダクタンス\(L\)とキャパシタンス\(C\)の値が小さければ共振周波数は低く、大きければ高くなります。
位相の周波数特性
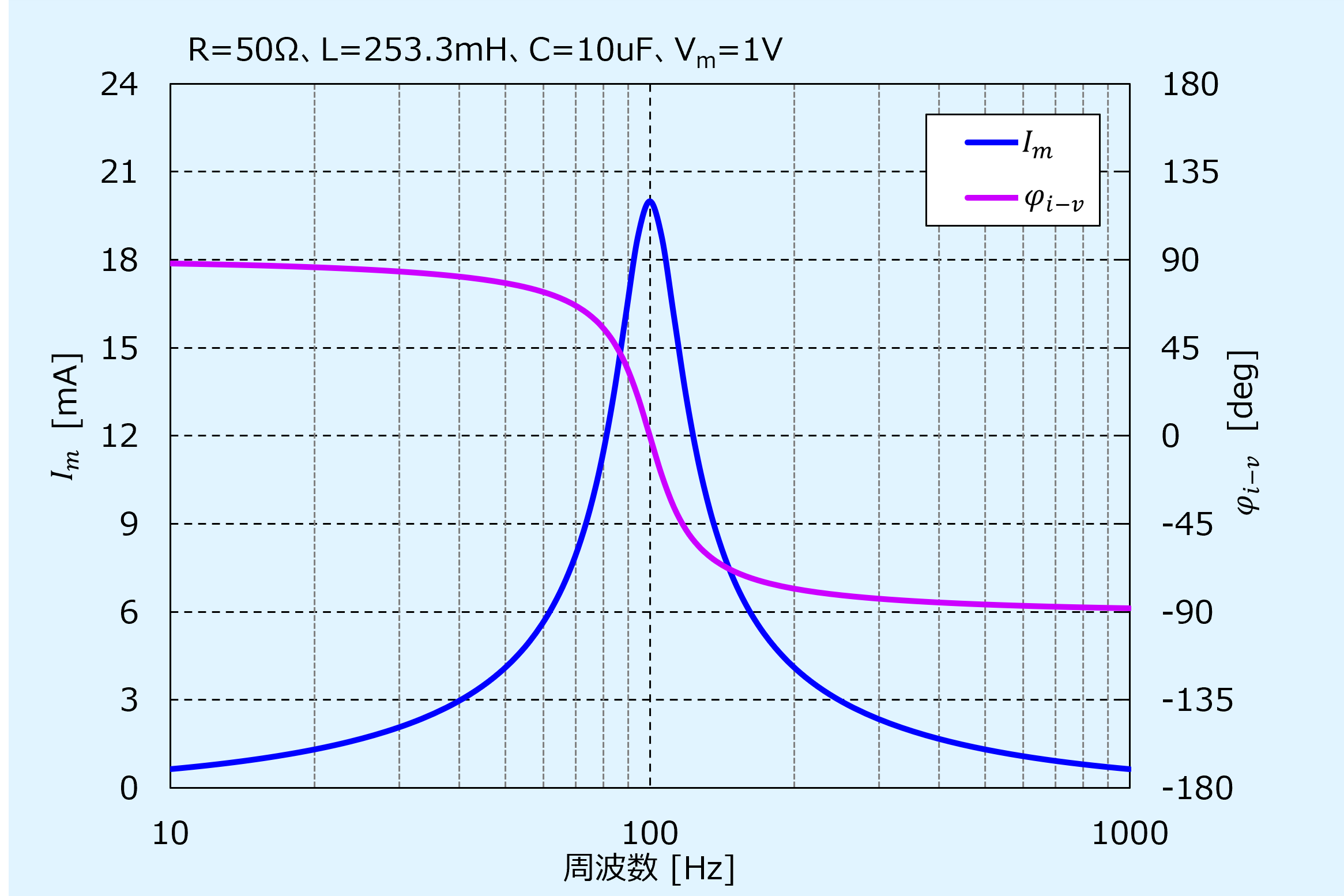
最後に電圧と電流の位相差\(\varphi_{i-v}\)の周波数特性を以下に示します。
比較として、電流の最大振幅\(I_m\)も合わせて表示しています。
周波数が低い領域では容量性が優勢であるため位相が進み、高い領域では誘導性が優勢のため位相が遅れます。
そして、共振点で電流と電圧の位相差は無くなり同相となります。
共振点を正確に求めるには振幅のピークを探すより、位相が0になる点を探す方が正確に求まります。
その他
電気回路全般については以下をご覧下さい。




コメント