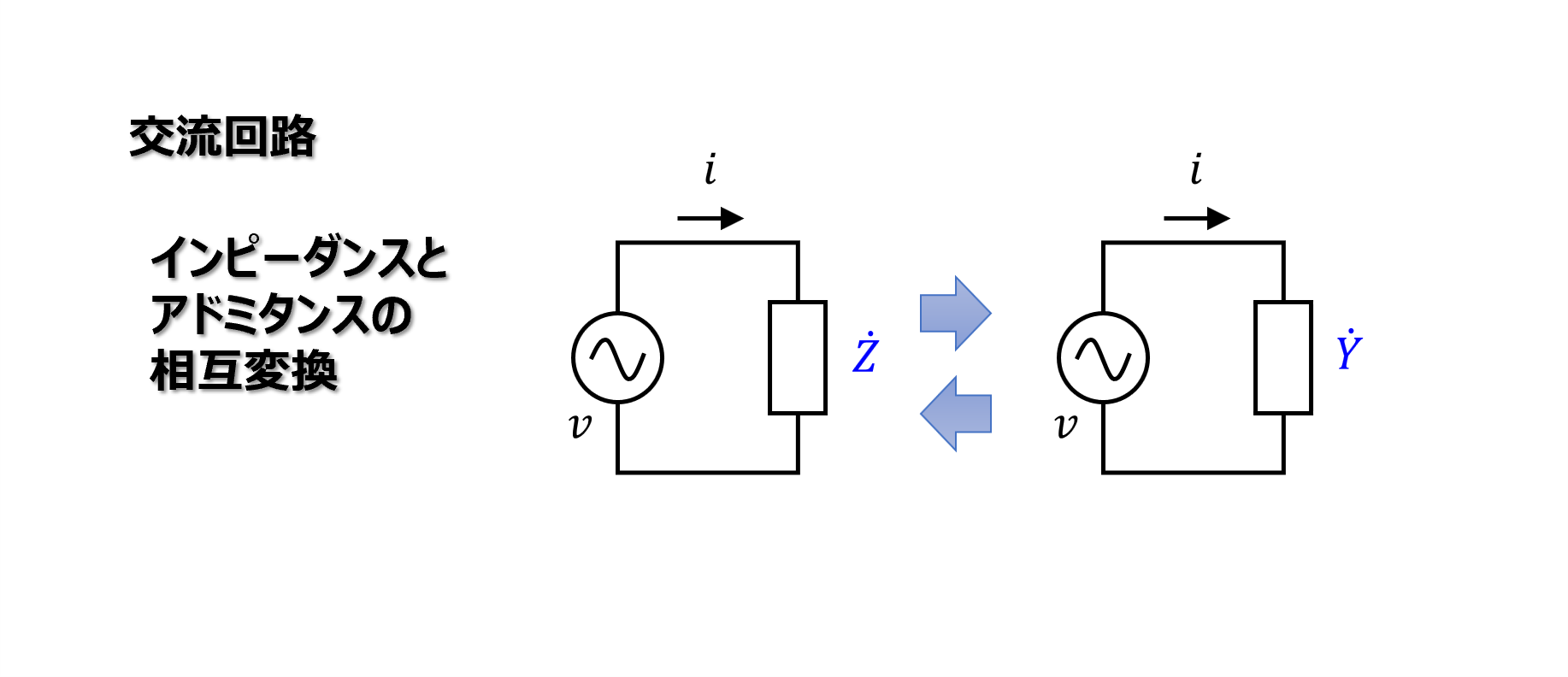
この記事では電気回路におけるインピーダンスとアドミタンスの相互変換について説明をします。
それぞれの要素間の相互変換から、複素数であるインピーダンスとアドミタンスの変換までを扱います。
目次
【まとめ】インピーダンスとアドミタンスの相互変換
最初にまとめです。
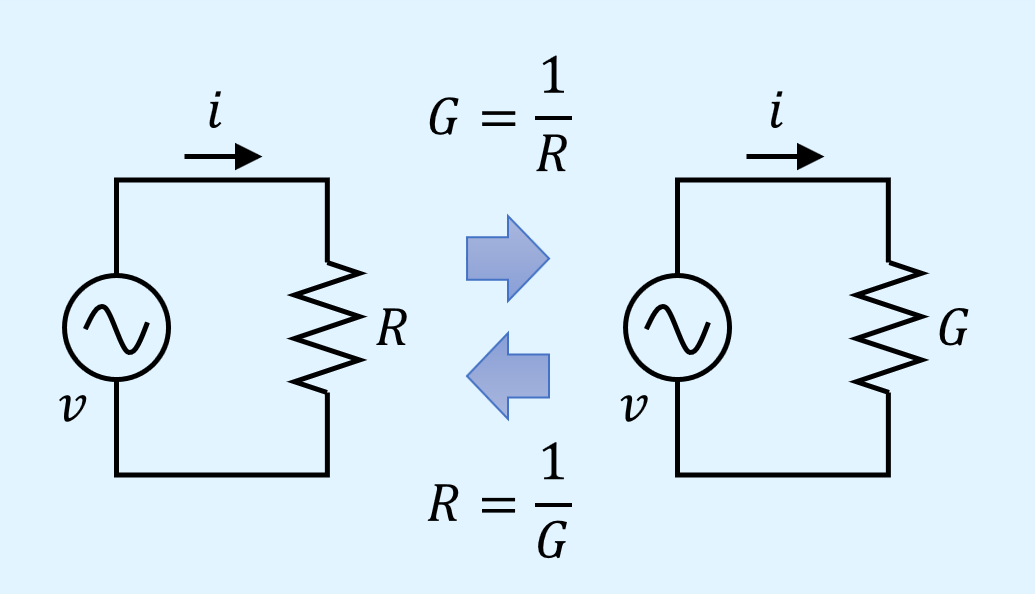
抵抗とコンダクタンスの相互変換
抵抗\(R\)をコンダクタンス\(G\)に変換する、逆に、コンダクタンス\(G\)を抵抗\(R\)に変換するには逆数を取るだけで済みます。
リアクタンスとサセプタンスの相互変換
リアクタンス\(X\)をサセプタンス\(B\)に変換する、逆に、サセプタンス\(B\)をリアクタンス\(X\)に変換するには逆数を取るだけで済みます。
インピーダンスをアドミタンスに変換
インピーダンス\(\dot{Z}\)をアドミタンス\(\dot{Y}\)に変換するには、逆数を取ればよいです。
インピーダンス\(\dot{Z}\)は複素数であるため、以下のように式変形を行い、コンダクタンス\(G\)とサセプタンス\(B\)を求めます。
コンダクタンス\(G\)とサセプタンス\(B\)のそれぞれで逆数を取ると、抵抗\(R_e\)とリアクタンス\(X_e\)を求めることができます。
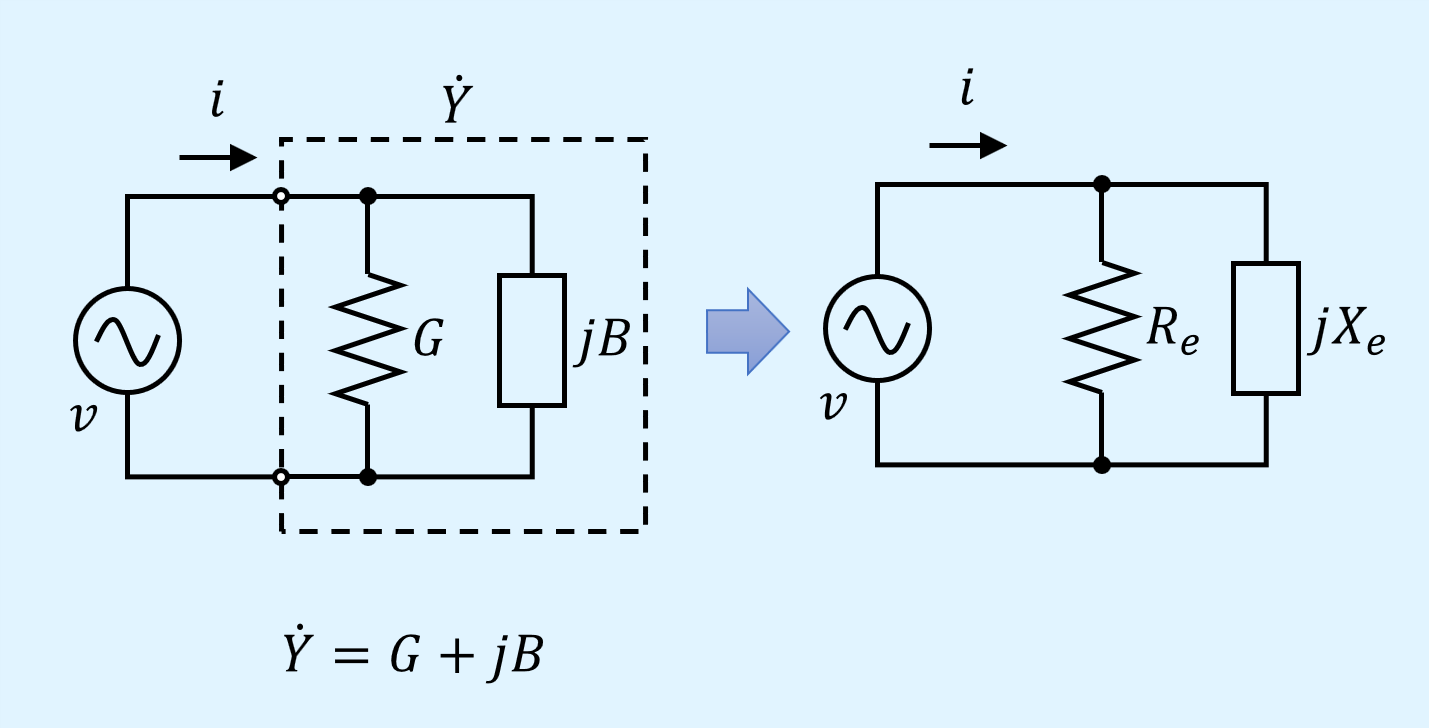
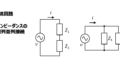
このように、インピーダンス\(\dot{Z}\)をアドミタンス\(\dot{Y}\)に変換することで、抵抗\(R_e\)とリアクタンス\(X_e\)の直列接続をそれと等価な抵抗\(R_e\)とリアクタンス\(X_e\)の並列接続に変換することができます。
抵抗\(R_e\)とリアクタンス\(X_e\)は次式で表されます。
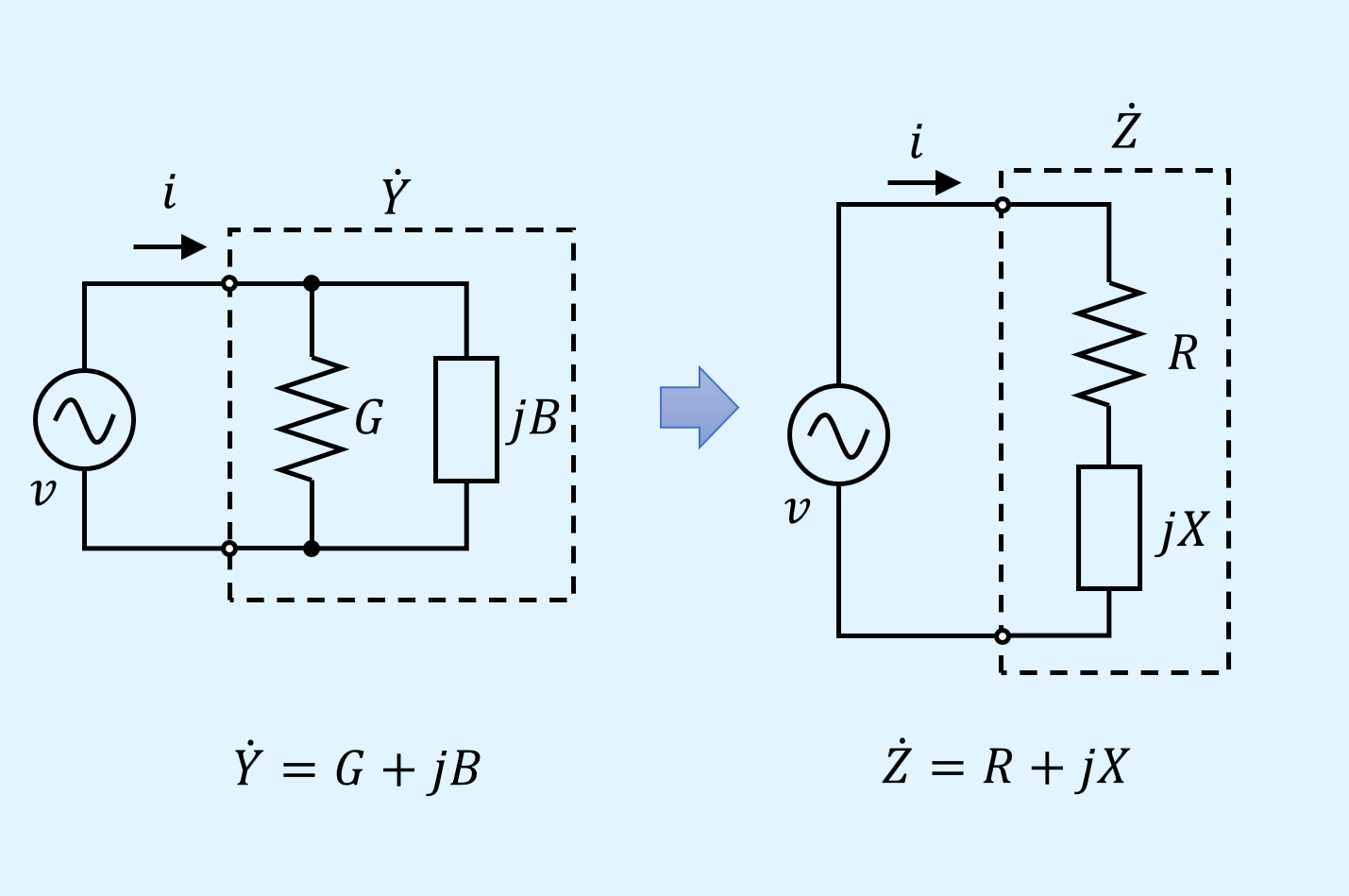
アドミタンスをインピーダンスに変換
今度は逆に、アドミタンス\(\dot{Y}\)をインピーダンス\(\dot{Z}\)に変換します。
同様に逆数を取ります。
アドミタンス\(\dot{Y}\)は複素数であるため、以下のように式変形を行い、抵抗\(R\)とリアクタンス\(X\)を求めます。
インピーダンスからアドミタンスに変換する際に、抵抗とリアクタンスの直列接続を等価な並列接続に変換できると説明しましたが、一応、アドミタンスからイピーダンスへの変換でも、コンダクタンスとサセプタンスの並列接続を等価な直列接続に変換することができます。
実用性はありませんが、以下に示します。
コンダクタンス\(G_e\)とサセプタンス\(B_e\)は次式で表されます。




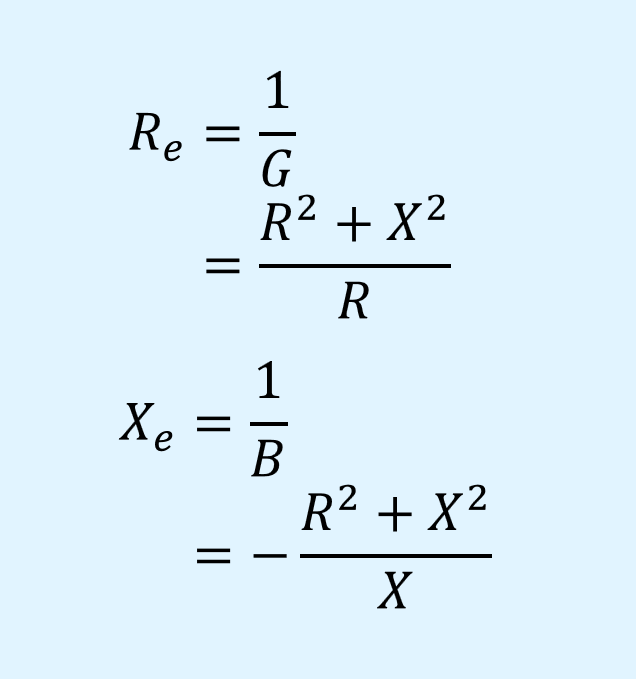
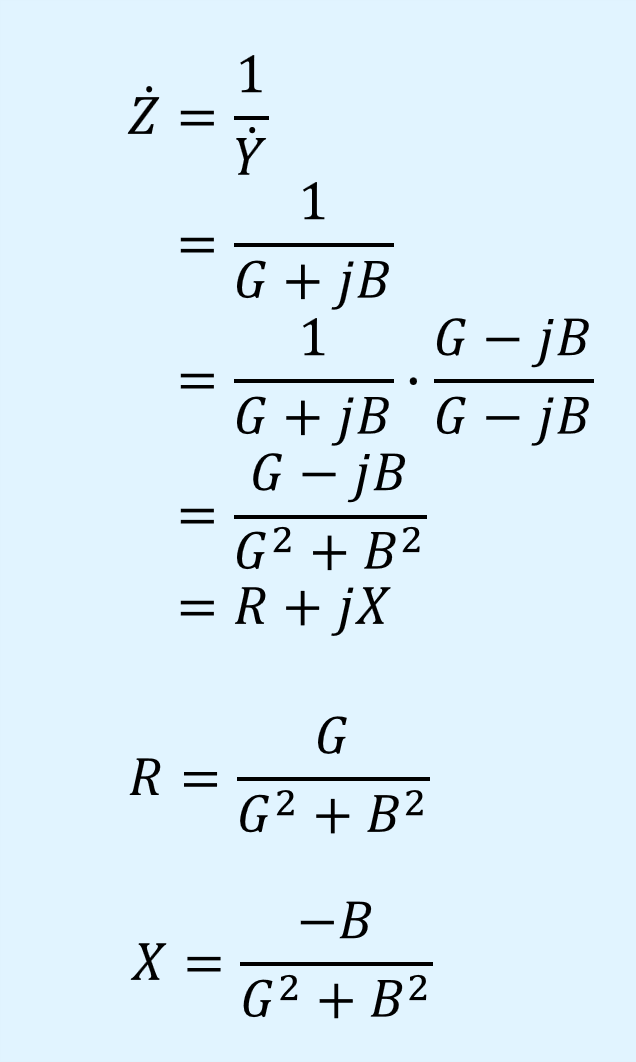

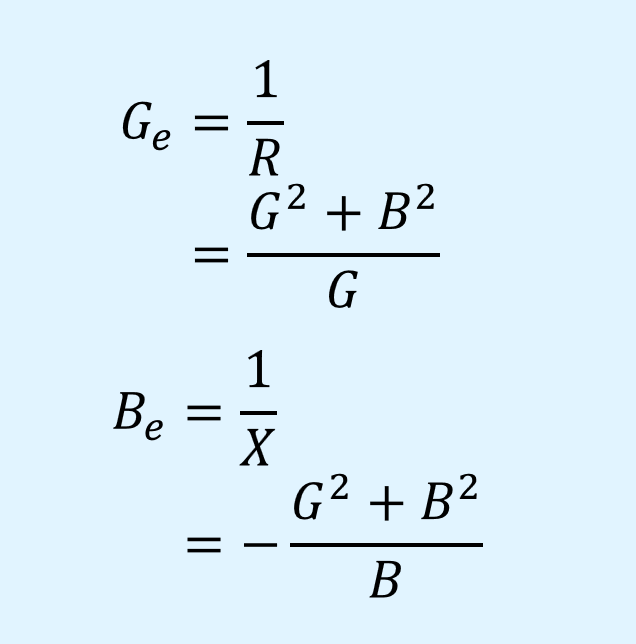
コメント