この記事では電気回路のアドミタンスについて説明をします。
アドミタンスとその構成要素から等価回路、ベクトル図、オームの法則との関係までを扱います。
【まとめ】アドミタンス
最初にまとめです。
アドミタンスとは
インピーダンスと対をなすものとして、アドミタンス(admittance)があります。
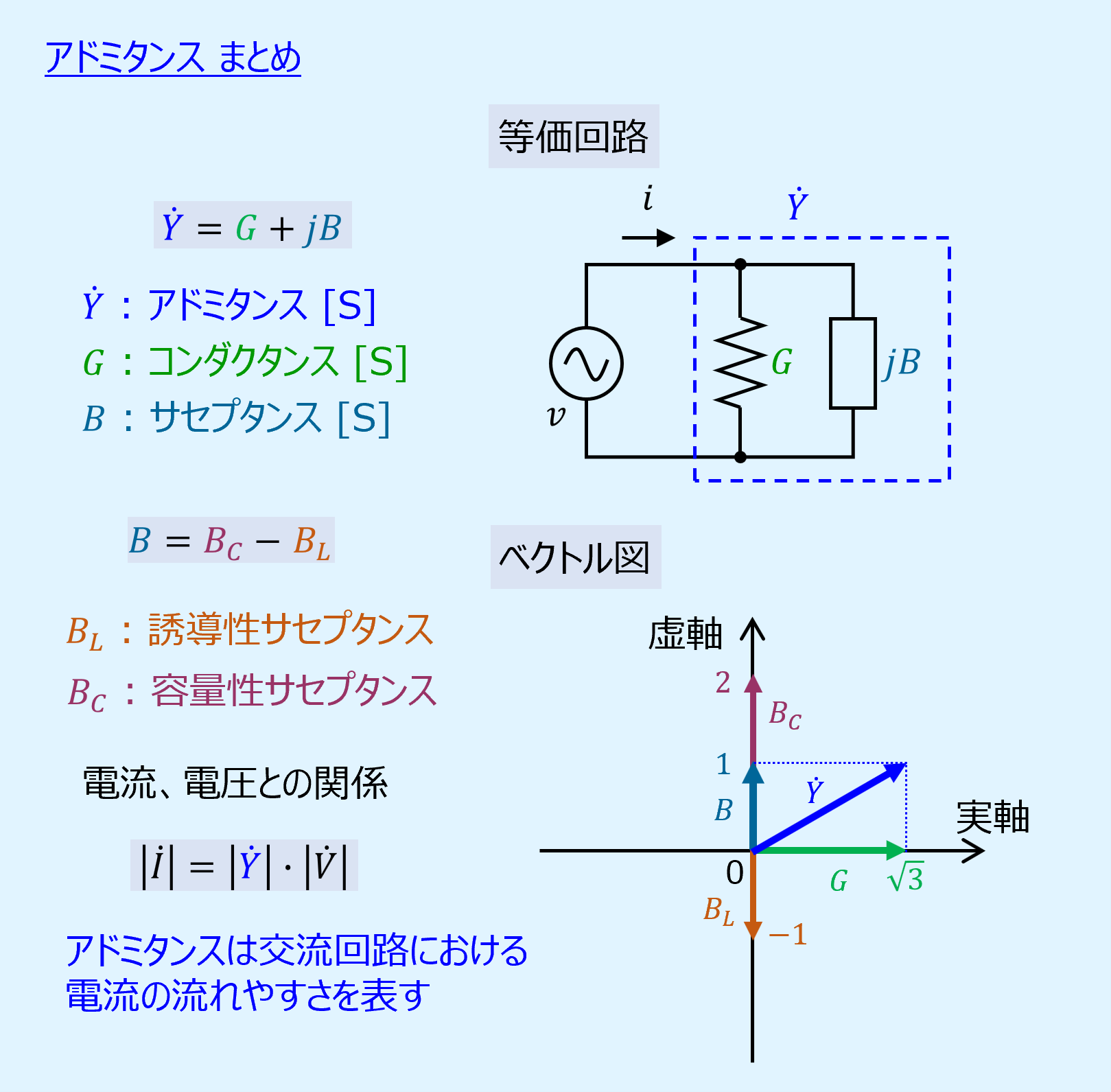
アドミタンスは実数部のコンダクタンス(conductance)と虚数部のサセプタンス(susceptance)から成る複素数です。
コンダクタンス\(G\)は抵抗\(R\)の逆数で、抵抗成分による電流の流れやすさを表したものです。
サセプタンス\(B\)はリアクタンス\(X\)の逆数で、交流回路において、インダクタンス成分とキャパシタンス成分による電流の流れやすさを表したものです。
また、アドミタンス\(\dot{Y}\)はインピーダンス\(\dot{Z}\)の逆数で、交流回路における抵抗成分、インダクタンス成分、キャパシタンス成分を全て含めた状態での電流の流れやすさを表すものです。
これらの関係を式として整理すると以下となります。
アドミタンス、コンダクタンス、サセプタンスは計算途中の物理量であり、最終的には逆数であるインピーダンス、抵抗、リアクタンスに戻されて使用されます。
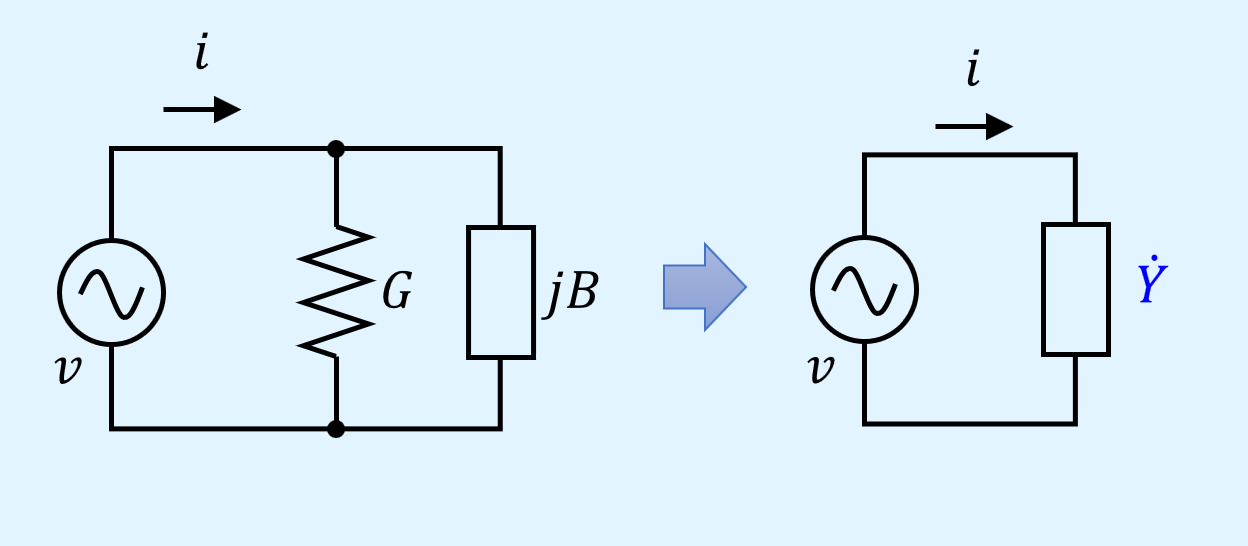
アドミタンスの等価回路
アドミタンス\(\dot{Y}\)の等価回路はコンダクタンス\(G\)とサセプタンス\(B\)の並列接続で表されます。
サセプタンスの内訳
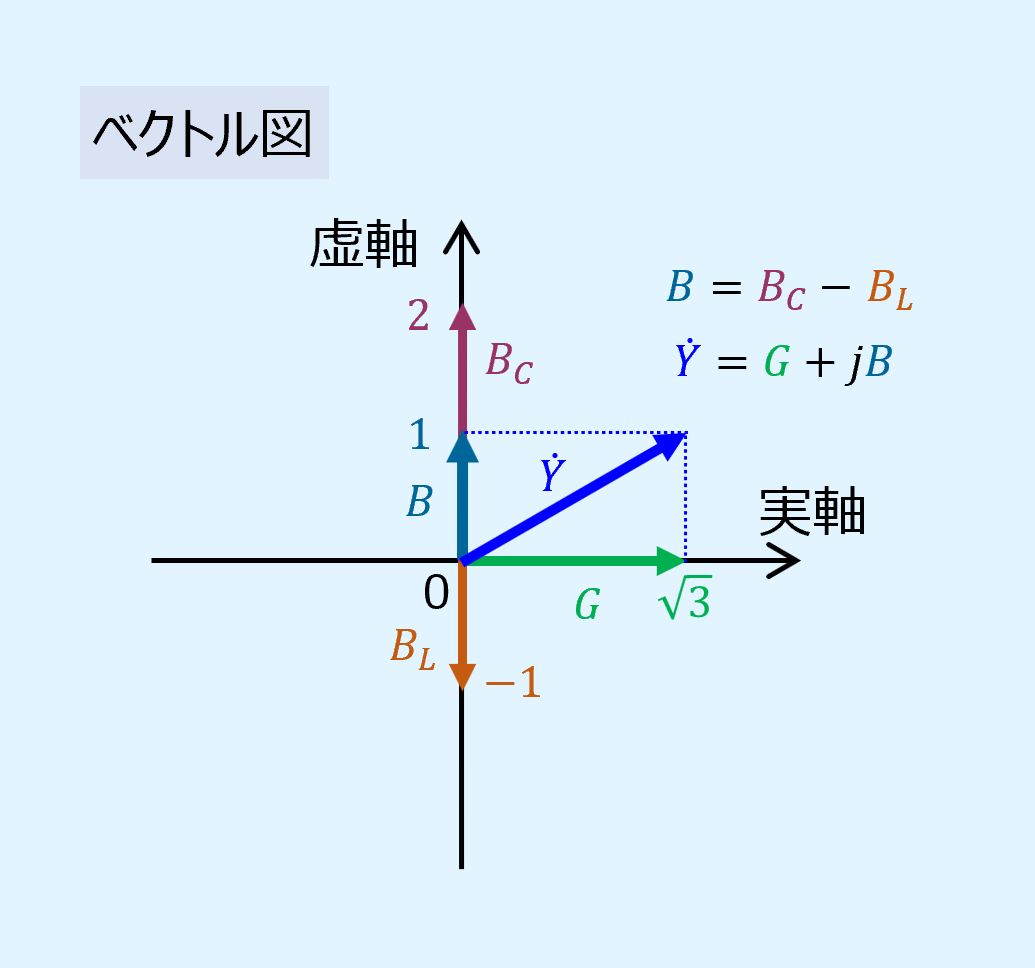
リアクタンスと同様に、サセプタンス\(B\)も誘導性と容量性から成り、容量性サセプタンス\(B_C\)から誘導性サセプタンス\(B_L\)を引いたものとなります。
正負の関係がリアクタンスとは逆になっており、容量性の方が大きい場合、サセプタンス\(B\)は正に、誘導性の方が大きい場合は負になります。
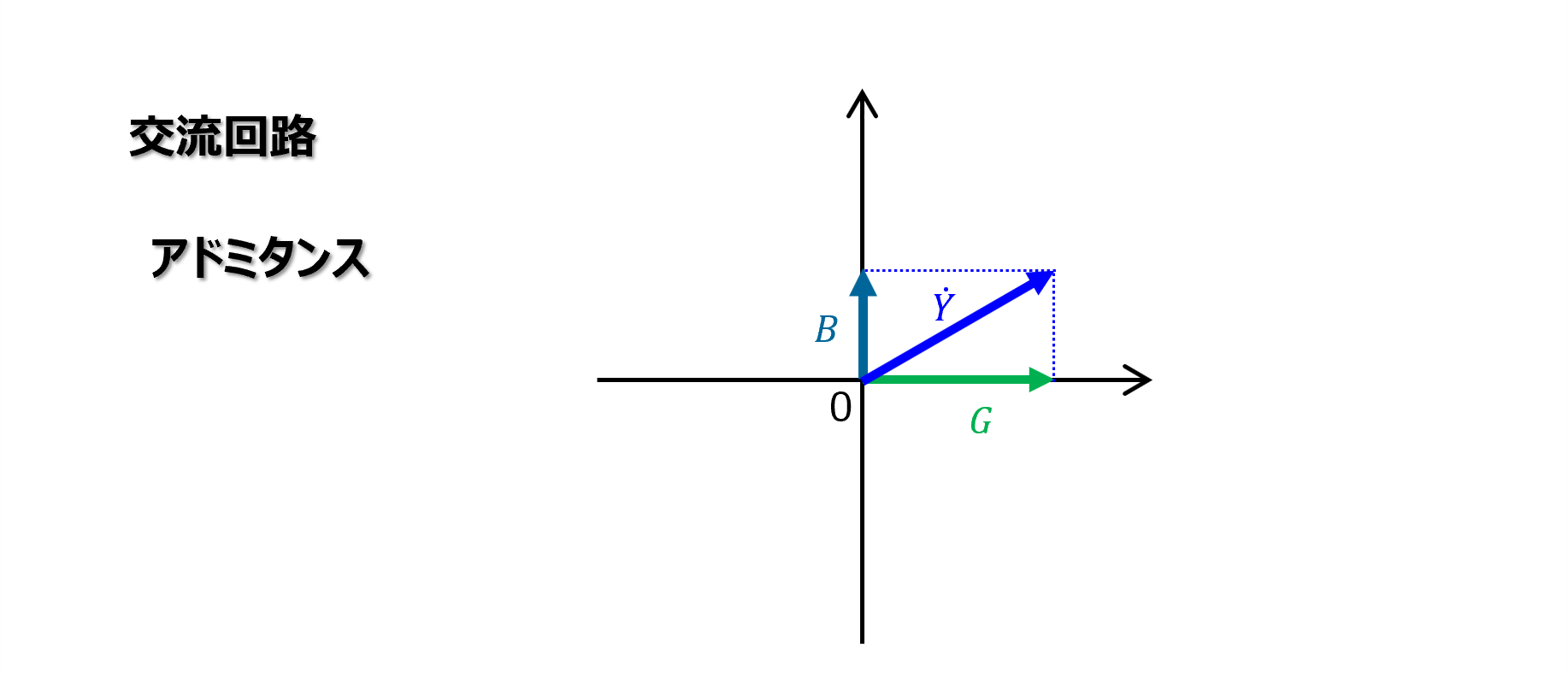
アドミタンスのベクトル図
インピーダンスと同様に複素平面上でベクトルとして図示することができます。
実軸にコンダンクタンス、虚軸にサセプタンスを当てはめます。
オームの法則との関係
アドミタンスについてもオームの法則が成り立ち、電圧、電流との関係をフェーザ\(|\dot{V}|\)、\(|\dot{I}|\)を用いて以下のように表すことができます。
こちらもインピーダンスとは逆の関係になっています。

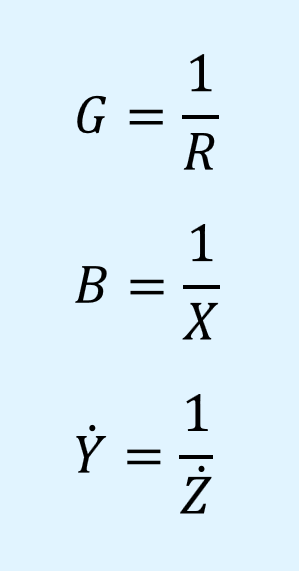

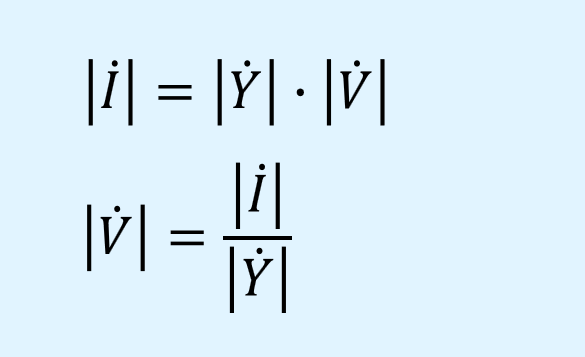
コメント