この記事では数学や情報処理で用いられる集合の演算則ついて説明をします。
式だけだとイメージが掴みにくいので、ベン図での説明も併記しています。
複雑な演算式を簡易な形に変えたり、取り扱いしやすい形に変えたりできますので、ぜひ覚えましょう。
ベン図でボリュームが増えてしまいましたので、記事は(1/2)と(2/2)で分割しています。
式だけだとイメージが掴みにくいので、ベン図での説明も併記しています。
複雑な演算式を簡易な形に変えたり、取り扱いしやすい形に変えたりできますので、ぜひ覚えましょう。
ベン図でボリュームが増えてしまいましたので、記事は(1/2)と(2/2)で分割しています。
【まとめ】集合演算則(1/2)
最初にまとめです。
はじめに
この記事では集合演算則の一部である恒等/統治/べき等/対合則の4つについて説明します。
また以降の説明で使われている記号\(A\)は任意の集合、\(U\)は全体集合、\(\phi\)は空集合を表しています。
恒等則
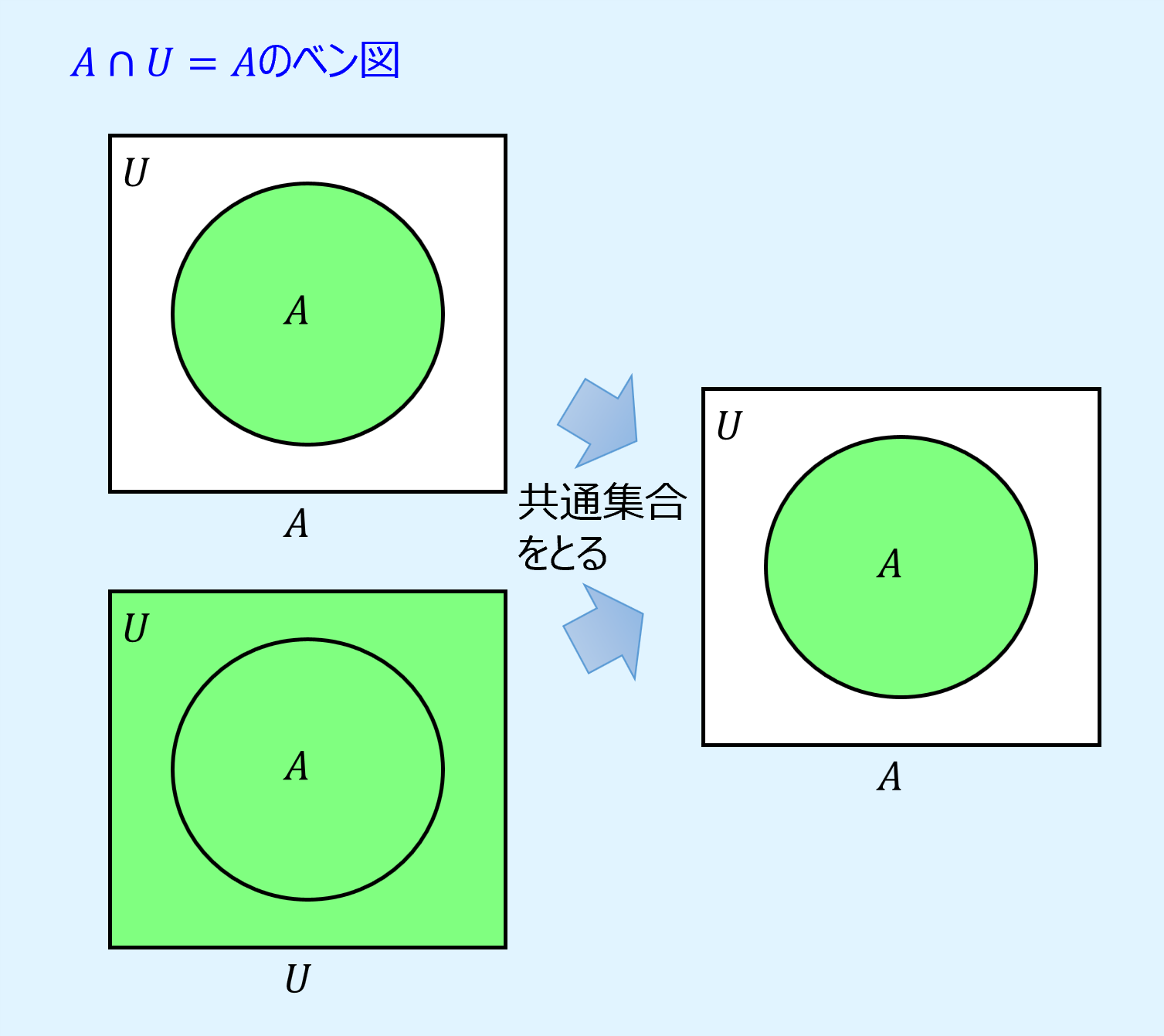
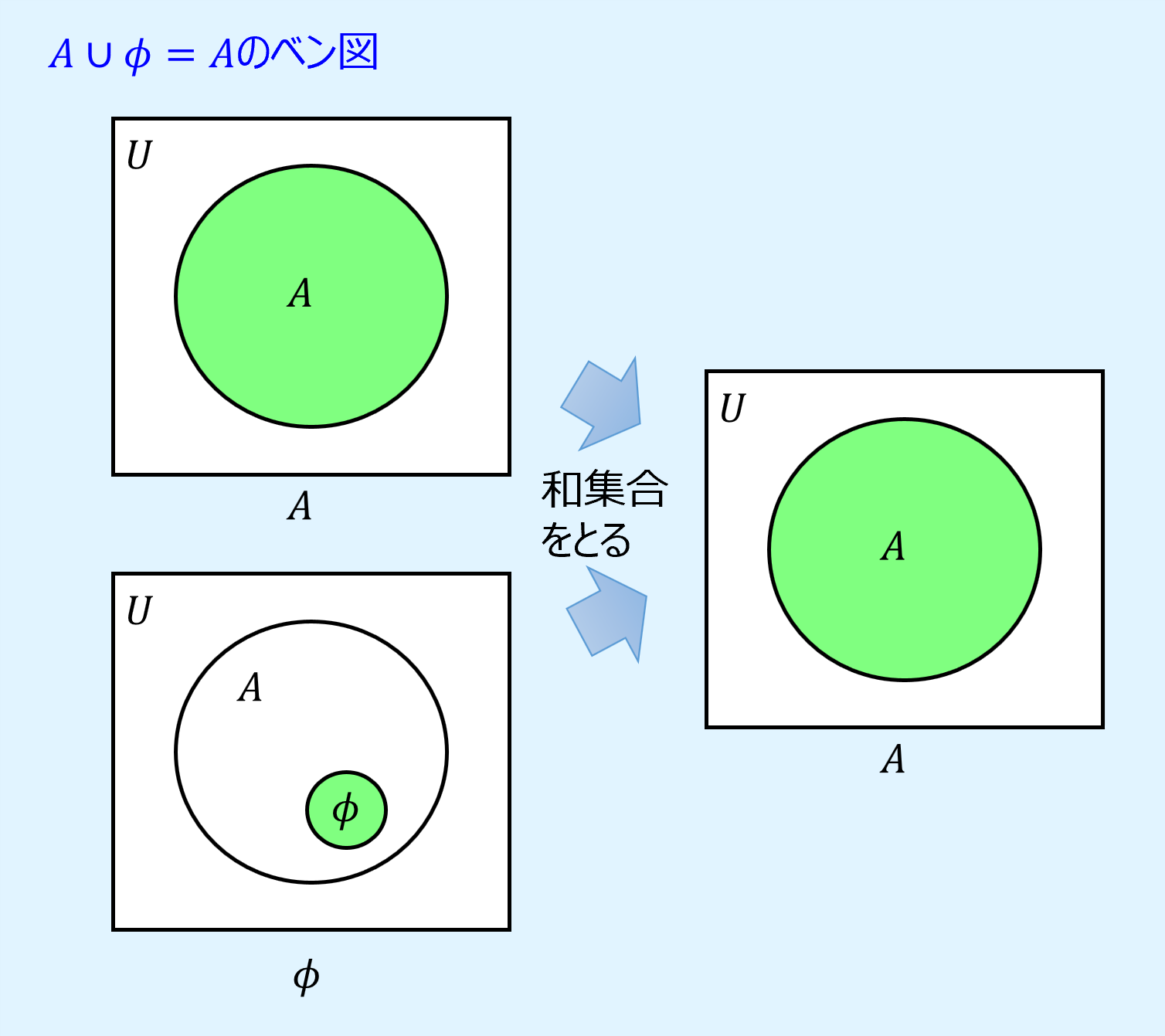
恒等則(identity laws)は、Aについて、全体集合\(U\)と共通集合をとっても、空集合\(\phi\)と和集合をとってもAのまま変わらないという演算則です。
数式で以下のように表されます。
また、ベン図を用いて表すと以下のようになります。
統治則
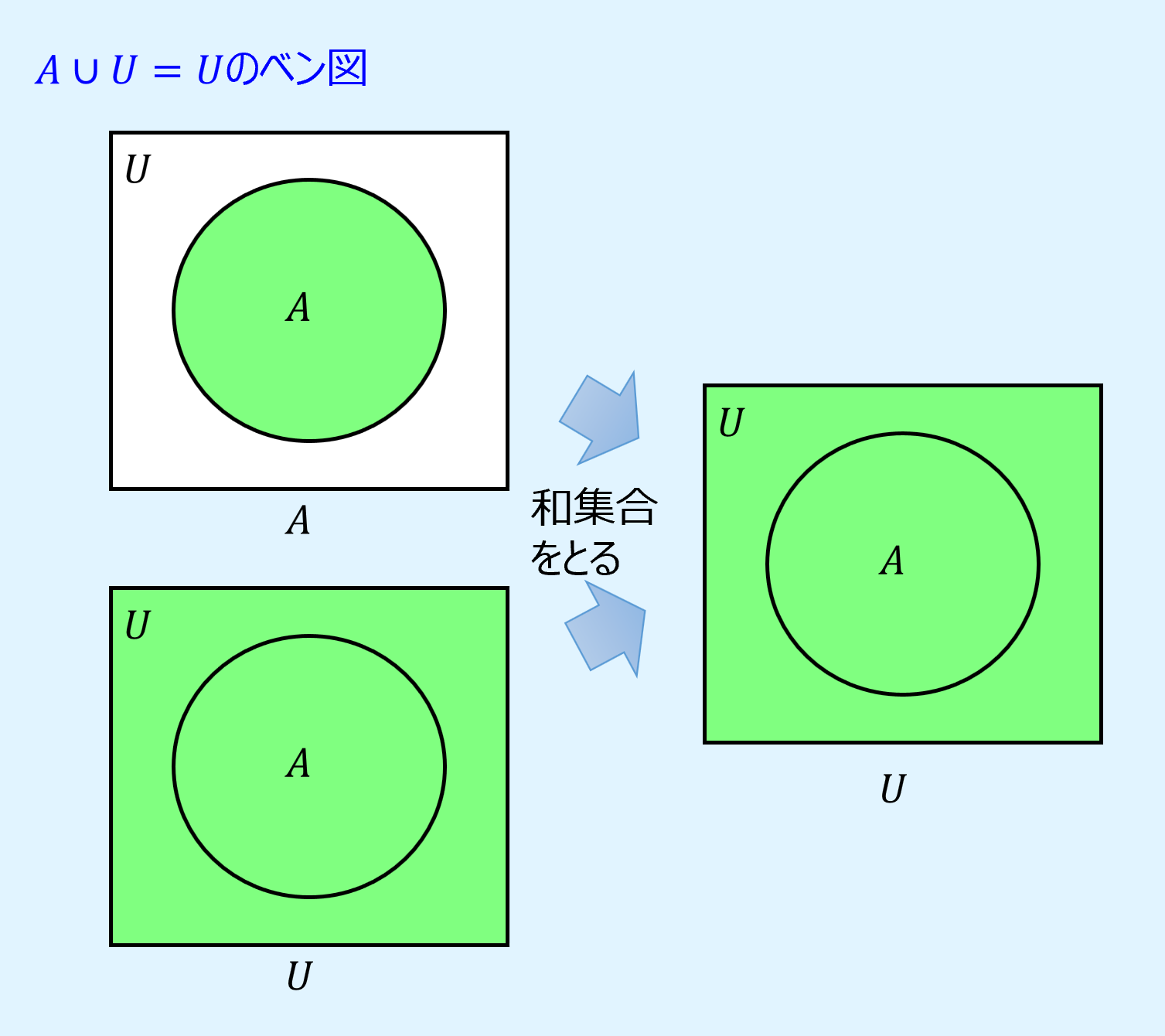
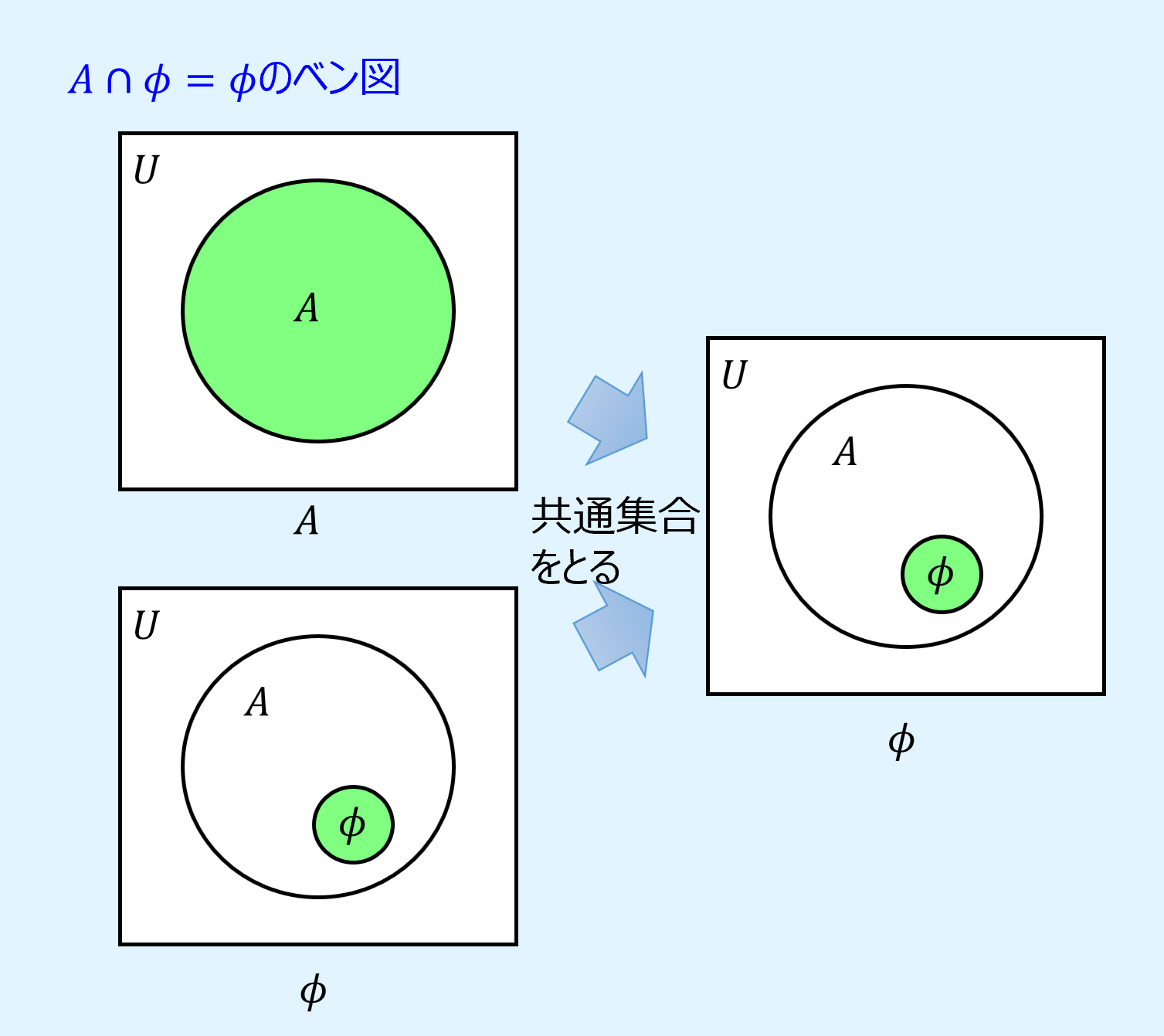
統治則(domination laws)は、Aについて、全体集合\(U\)と和集合をとると全体集合\(U\)に、空集合\(\phi\)と共通集合をとると空集合\(\phi\)になるという演算則です。
数式で以下のように表されます。
また、ベン図を用いて表すと以下のようになります。
べき等則
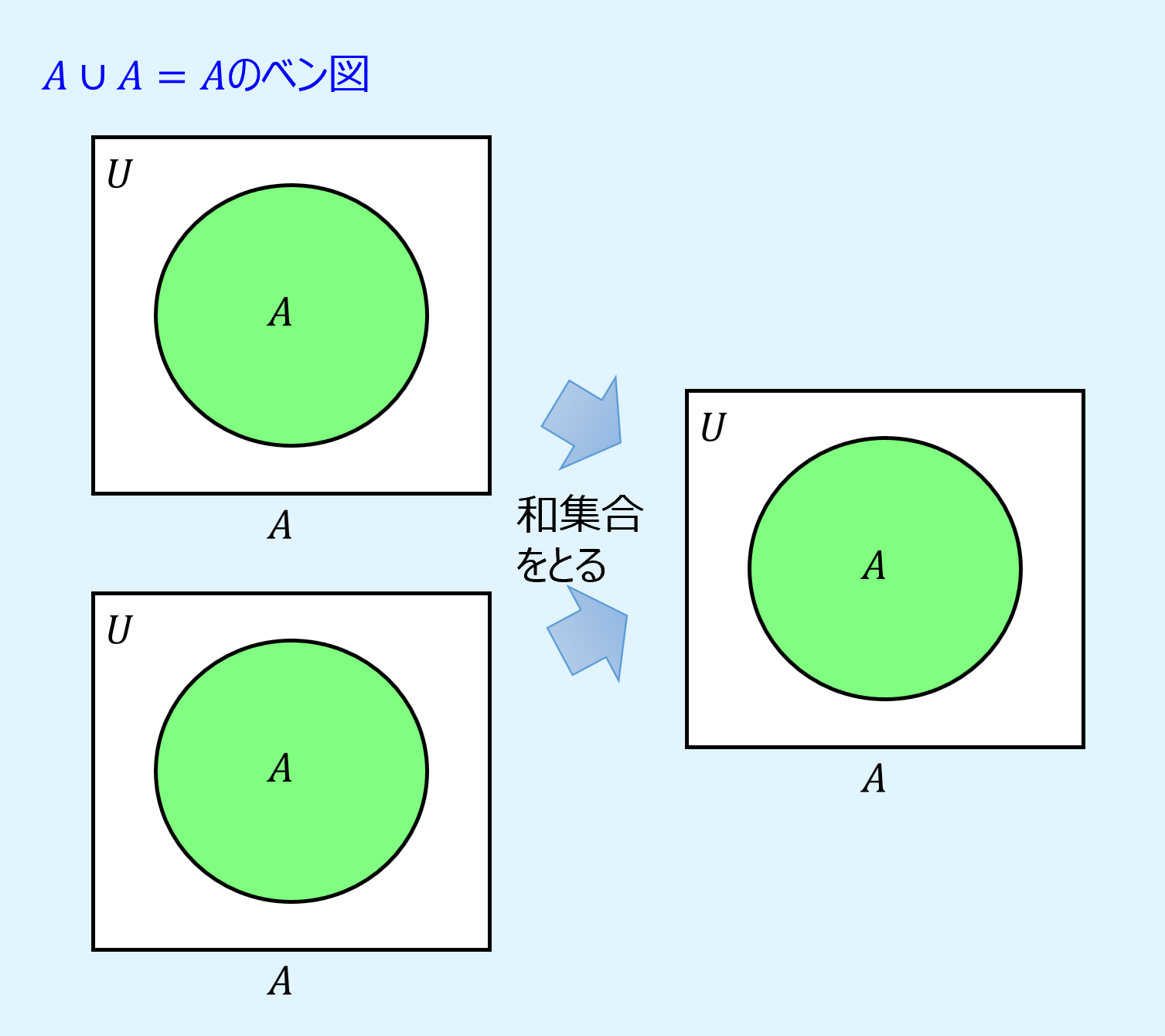
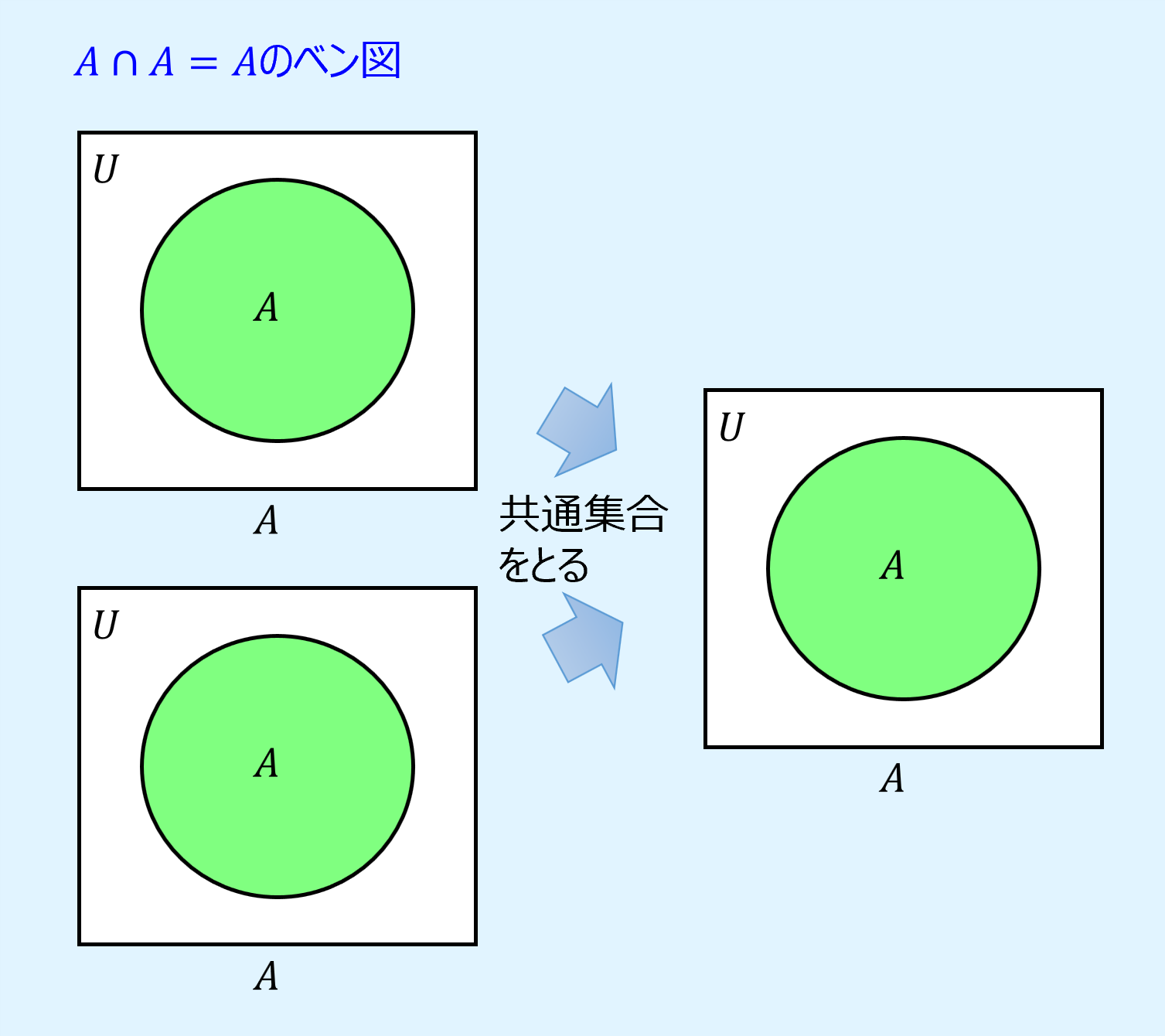
べき等則(idempotent laws)は、自身の集合同士の和集合、共通集合は自身の集合になるという演算則です。
「べき等」は数学用語で、ある操作を1回行っても複数回行っても結果が分からない性質を意味します。
数式で以下のように表されます。
また、ベン図を用いて表すと以下のようになります。
対合則
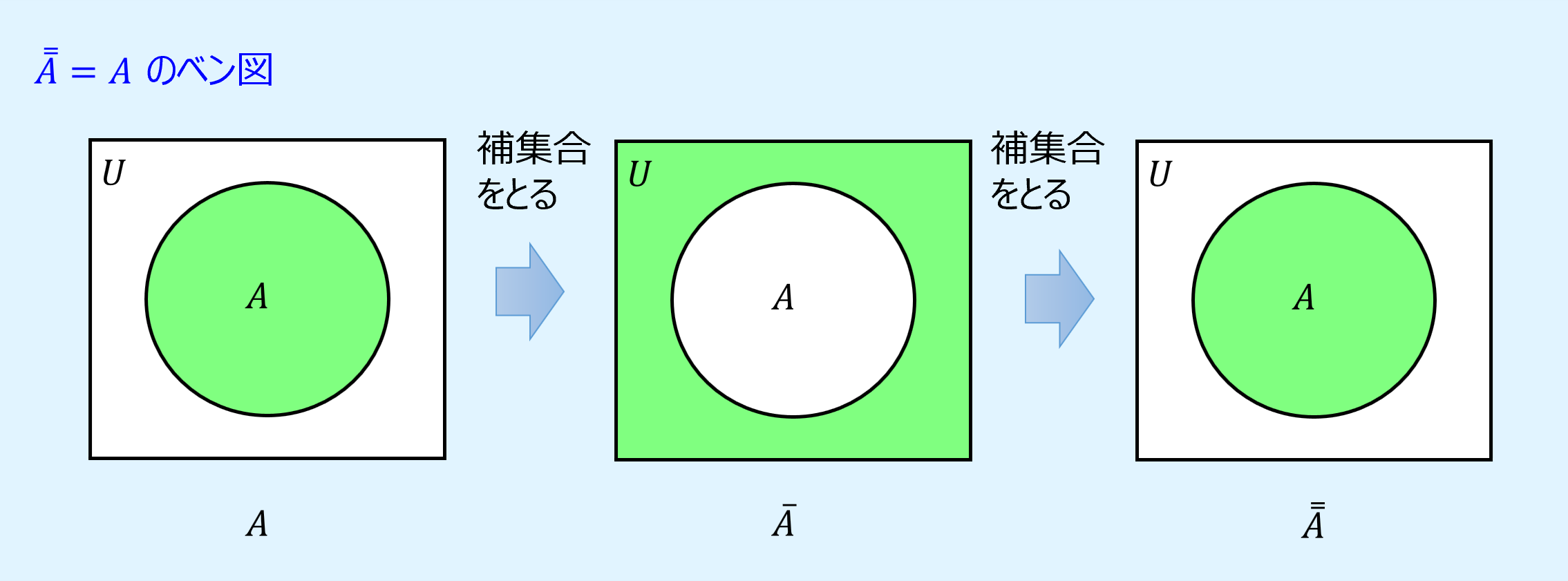
対合則(involution law, complementation law)は、補集合の補集合は元の集合になるという演算則です。
数式で以下のように表されます。
また、ベン図を用いて表すと以下のようになります。
残りの演算則
残りは次回の記事に記載します。
おわりに
恒等/統治/べき等/対合則の4つについて、数式とベン図で説明しました。
いずれも簡単で、法則とするほどなのかと思われるかも知れませんが、複雑な演算式を変形する際に使用しますので、しっかりと覚えましょう。


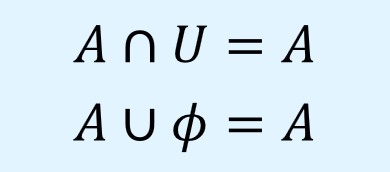
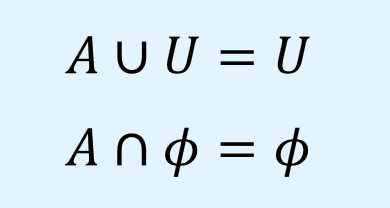
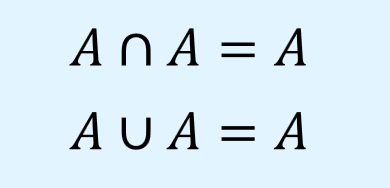
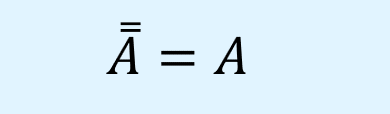


コメント